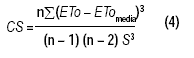Serviços Personalizados
Journal
Artigo
Links relacionados
Compartilhar
Agrociencia (Uruguay)
versão impressa ISSN 1510-0839versão On-line ISSN 2301-1548
Agrociencia Uruguay vol.19 no.1 Montevideo jun. 2015
Determinación de la evapotranspiración del cultivo de referencia (ETo) para el diseño de equipos de riego en el Uruguay
García Petillo Mario(†)1, Puppo Lucía1
1Departamento de Suelos y Aguas, Facultad de Agronomía, Universidad de la República. Garzón 780, 12900 Montevideo, Uruguay. Correo electrónico: lpuppo@fagro.edu.uy
Recibido: 16/6/14 Aceptado: 6/2/15
Resumen
La evapotranspiración del cultivo de referencia (ETo) máxima es el dato de partida para el diseño de los sistemas de riego. Con este valor se determina el caudal de diseño que permite definir el equipo más económico que asegure el crecimiento potencial de los cultivos. El concepto de ETo máxima no es un valor único como lo sería el máximo absoluto, sino que varía de acuerdo al período considerado (diario, semanal, decádico, mensual) y a la probabilidad de no excedencia considerada. En este trabajo se analizaron series históricas de valores diarios de ETo del mes de enero, de entre 28 y 35 años, registradas en las cinco estaciones experimentales del Instituto Nacional de Investigación Agropecuaria (INIA). El valor de la ETo diaria con un 80 % de probabilidad de no excedencia fue sensiblemente mayor a las calculadas en base a datos decádicos o mensuales. Estas dos últimas fueron similares entre sí, variando entre 0,1 a 0,3 mm d-1 en las diferentes estaciones experimentales. En el sur del país (Canelones y Colonia) se pueden dar días con una ETo tan alta como en el norte (Salto), pero en Salto las altas ETo se mantienen durante lapsos más prolongados. El objetivo de este trabajo fue recomendar un valor de ETo a utilizar para el diseño de los equipos de riego en cualquier lugar del país. Para ello se presenta un mapa del Uruguay con las isolíneas de ETo calculada en períodos decádicos con un 80 % de probabilidad de no excedencia.
Palabras clave: DEMANDA ATMOSFÉRICA, CAUDAL DE DISEÑO, PROBABILIDAD DE OCURRENCIA, ISOLÍNEAS DE ETO
Summary
Determination of the Reference Crop Evapotranspiration (ETo) for Designinig Irrigation Equipment in Uruguay
The maximum reference crop evapotranspiration (ETo) is the starting point for irrigation systems design. With this value it is posible to calculate the design flow which leads to the most economic equipment that ensures the potential crop growth. The concept of maximum ETo is not a single value as would be the absolute maximum, but varies according to the period considered (daily, weekly, decadal, monthly) and the probability of non-exceedence. In this paper daily ETo time series, between 28 and 35 years, recorded in January at the five experimental stations of National Institute of Agricultural Research (INIA) were analyzed. Daily ETo values with 80 % probability of non-exeedence were significantly higher than those calculated based on decadal or monthly data. The latter two were quite similar, ranging from 0.1 to 0.3 mm d-1 in the different experimental stations. In the south (Canelones and Colonia), daily ETo values were as high as in the north (Salto), but in Salto the ETo values remained higher for longer periods. The aim of this study was to recommend an ETo value which can be used for irrigation equipment design anywhere across the country. As a result, a map of Uruguay with ETo isolines based on decadal data with 80 % probabilityof non-exceedence is presented.
Keywords: ATMOSPHERIC DEMAND, DESIGN FLOW, PROBABILITY OF OCCURRENCE, ETO ISOLINES
Introducción
El conocimiento de la evapotranspiración de los cultivos (ETc) es esencial para un manejo eficiente del riego ajustando el volumen y la frecuencia del riego a los requerimientos de los cultivos. Un manejo correcto del riego permite apuntar a rendimientos altos, con estabilidad entre años, y a una calidad óptima del producto cosechado, haciendo posible un uso racional del agua y de la energía, minimizando el desperdicio de ambos recursos y la contaminación del medio ambiente. Asimismo este dato es fundamental para un correcto diseño de los sistemas de riego (Puppo y García Petillo, 2010).
Desde hace varios años el método FAO Penman-Monteith (PM-FAO) es considerado el método estándar tanto para la definición como para el cálculo de la evapotranspiración del cultivo de referencia (ETo) (Allen et al., 1998).
El concepto de ETo máxima para una serie histórica de datos no es un valor único como lo sería el máximo absoluto, sino que varía de acuerdo al período considerado (diario, semanal, decádico, mensual) y a la probabilidad de no excedencia considerada. Cuando el objetivo es el diseño de un sistema de riego la ETo máxima permite definir el caudal de diseño y con este la capacidad mínima de bombeo y conducción que aseguren el crecimiento potencial de los cultivos.
En la medida en que el intervalo entre riegos es más corto –riegos de alta frecuencia– la ETo máxima aumenta y el análisis de los valores conviene realizarlo a partir de series históricas con datos diarios (Pizarro, 1990; Allen et al., 2007). Según Allen et al. (2007) la ETo utilizada para el diseño en los sistemas con intervalo de riegos de tres días, en Kimberly (Idaho), fue un 9 % mayor que para los sistemas con intervalo de riego de 30 días.
El porcentaje de no excedencia es definido como el valor de ETo que se espera que no sea excedido el p % del tiempo, donde p es el nivel de probabilidad.
Según Pizarro (1990) además de la variación climática interanual existe otra diaria, pudiendo presentarse días con necesidades mayores a las medias mensuales o medias decádicas cuando la ETo de partida no se ha calculado día por día. Para el diseño de riegos de alta frecuencia este autor recomienda la utilización de un coeficiente de 1,2 para incrementar la ETo cuando el valor de partida sea el valor medio mensual correspondiente al mes de máximo requerimiento hídrico del cultivo.
En este mismo sentido Allen y Wright (1983) verificaron un gran decrecimiento de la variabilidad a medida que el período considerado para los cálculos aumentaba al calcular la distribución de ETo diaria y mensual en Kimberly, Idaho, en una serie de 14 años.
Para conocer la magnitud y probabilidad de ocurrencia de los valores extremos de ETo de enero (mes de máxima demanda) es conveniente realizar un análisis de frecuencias acumuladas con los datos medios correspondientes a períodos de riego similares a los intervalos de riego previstos en el proyecto, eligiendo un nivel de porcentaje de no excedencia adecuado (Galeazzi y Lutz, 2008; Allen et al., 2007).
Asumiendo que la ETo tiene una distribución normal, la estimación de la ETo para una probabilidad específica de no excedencia se calcula como (Allen et al., 2007):
donde EToPn es el valor de ETo que se espera sea excedido sólo el 100-p % del tiempo, KPn es un factor de probabilidad y ETomedia y S son los estimadores de la media y el desvío estándar. Los valores de KPn se presentan en el Cuadro 1.

Según Allen et al. (2007) se requiere una serie mínima de cinco años de registros diarios para obtener estimaciones válidas de ETomedia, S y EtoPn.
Generalmente estos valores son computados para un período de tiempo determinado durante la estación de crecimiento, por ejemplo para el período de máxima demanda de 30 días. Tomando el mes de enero como representativo del periodo crítico a los fines del diseño y operación de proyectos, Galeazzi y Lutz ( ) en el Alto Valle del Río Negro, Argentina, constataron un incremento del 17 % en el valor de la ETo al considerar una probabilidad de no excedencia del 90 % frente al valor medio mensual.
En la provincia de Villa Clara, Cuba, Ávalos y Pacheco Seguí (2012) recomiendan usar la ETo mensual con 75 % de probabilidad de no excedencia para diseñar el riego de caña de azúcar.
La relación del valor de ETo con 75 % de probabilidad de no excedencia (para riegos frecuentes) y del valor de ETo medio mensual es mayor cuanto mayor la variabilidad en nubosidad durante el mes de máximo requerimiento hídrico. El valor de esta relación es aproximadamente 1,4 para climas húmedos y sub húmedos como el de Uruguay (Doorenbos y Pruitt, 1977).
La probabilidad de no excedencia recomendada por diferentes autores varía entre 75 % para cultivos extensivos (Ávalos y Pacheco Seguí, 2012) y 90 % para cultivos intensivos. Cuanto mayor sea la probabilidad utilizada, más seguro es el equipo pero también son mayores sus costos de inversión.
En nuestro país, durante la última década el riego se ha extendido a los cultivos extensivos de verano y pasturas, además de los cultivos intensivos regados tradicionalmente. Esto ha determinado que el riego se haya ampliado a todo el país. Hasta el momento es una práctica común el diseño de los equipos a partir del dato de ETo promedio mensual del mes de máxima demanda (enero), lo cual podría conducir a equipos limitados en su caudal con la posibilidad de ocurrencia de déficits hídricos en etapas críticas del cultivo. Una alternativa sería utilizar valores de ETo promedio para períodos más cortos de tiempo, decádicos o diarios, analizando distintos porcentajes de no excedencia. Por lo cual se plantea como objetivo de este trabajo determinar el valor de ETo PM-FAO que se debería recomendar, como dato inicial para el diseño de los sistemas de riego del Uruguay apuntando a obtener la máxima respuesta productiva.
Materiales y métodos
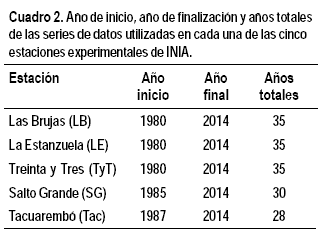
Se analizaron los datos diarios de ETo PM-FAO del mes de enero, de las cinco estaciones experimentales del Instituto Nacional de Investigación Agropecuaria (INIA), en las siguientes series de años (Cuadro 2). El análisis se limitó a los datos de estas estaciones experimentales, porque son estaciones agrometeorológicas donde los instrumentos de medición están sometidos a un balance energético similar al que afecta a los cultivos de cada zona, respetando las condiciones recomendadas para su instalación y por otra parte proporcionan datos confiables debido a los controles periódicos de calidad de los mismos (Allen et al.,1998).
Las estaciones experimentales de INIA tienen la siguiente ubicación (Cuadro 3):
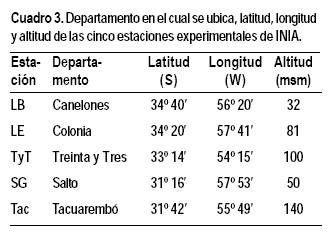
Se calculó la ETo en períodos de 10 días de cada mes (ETo decádica). Para esto se hizo el promedio de las ETo registradas del día 1 al 10 (primera década), del 11 al 20 (segunda década) y del 21 al 31 (tercera década). Es decir, que la tercera década tenía en realidad 11 días.
Se calculó la ETo media de cada mes (ETo mensual) haciendo el promedio de los valores de los 31 días del mes.
Se calculó el desvío estándar (S) como:
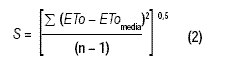
donde ETomedia es el promedio de los registros de ETo para el período evaluado (diaria, decádica y mensual) y n el número de registros. De acuerdo a lo anterior, se dispuso de las cantidades de registros que se detallan en el Cuadro 4.
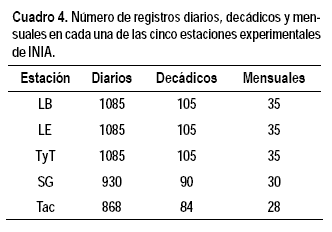
En definitiva, se elaboraron 15 series de datos (diarios, decádicos y mensuales para cada una de las cinco estaciones experimentales de INIA). Cada una de estas 15 series se ordenó de menor a mayor, se les adjudicó un número de orden (1 al menor valor, N al mayor valor), y se calculó la probabilidad (p) de cada valor utilizando la Ecuación 3. Los valores de N son los que se muestran en el Cuadro 4.
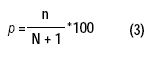
donde p la probabilidad (en %), n el número de orden y N el número total de registros.
A partir de este cálculo se determinó el valor de ETo para diferentes probabilidades de que se registre un valor igual o menor a ese. Adicionalmente, para cada estación experimental se calculó la ETo media, haciendo el promedio de los valores diarios de toda la serie.
Para verificar la distribución normal de los datos de ETo de enero de las cinco estaciones se calculó el coeficiente de asimetría (CS) utilizando la Ecuación (4) (Coolidge, 2012).
donde n es el número de observaciones.
Se calculó la EToPn para una probabilidad de no excedencia del 80 % utilizando la Ecuación (1) y el coeficiente correspondiente del Cuadro 1.
Resultados y discusión
Se graficaron las curvas de distribución de frecuencias de la ETo PM-FAO diaria, en categorías de 0,5 mm. Dado que la ETo tiene un límite físico inferior = 0, y que ese límite en los hechos es de 1,6 mm d-1 (Figura 1), y que por el contrario no tiene un límite físico superior, los valores son más concentrados en la cola izquierda y más extendidos en la derecha.
Se analizó si a pesar de lo anterior la distribución cumple con las condiciones de normalidad, calculando el coeficiente de asimetría (Cuadro 5).
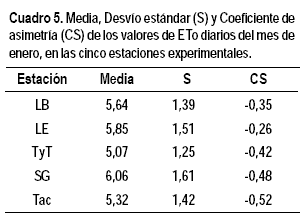
Los valores de coeficiente de asimetría varían entre -0,26 y -0,52. Cuando el valor del CS se encuentra entre -0,5 y 0,5 se asume que la distribución es normal, mientras que los valores inferiores o superiores a este rango corresponden a una distribución Pearson Type III.
A pesar que el CS para la estación de Tacuarembó está ligeramente fuera del rango de validez para la distribución normal se realizaron los cálculos aceptando como válida esta distribución. En este sentido Allen et al. (2007) calcularon los porcentajes de no excedencia de ETo bajo los supuestos de distribución normal y distribución Pearson Type III, encontrando diferencias mínimas entre los valores calculados con ambas distribuciones.
La distribución de probabilidades se presenta en la Figura 2.
Se observa en la Figura 2 que en el caso de los eventos extremos (p<20 % y p >80 %) las ETo diarias son mucho menores o mucho mayores, respectivamente, que las ETo calculadas en períodos decádicos o mensuales. Por el contrario, en los eventos más frecuentes (20 %<p<80 %) la ETo diaria, decádica o mensual es muy similar en Las Brujas, Treinta y Tres y Tacuarembó. Sin embargo, en La Estanzuela y Salto Grande las ETo diarias presentan diferencias en un rango más amplio de probabilidades.
La diferencia entre valores decádicos y mensuales no es muy importante, variando entre 0,1 mm d-1 o un 1,6 % en el caso de Las Brujas hasta 0,3 mm d-1 o un 4,6 % en el caso de Salto Grande.
Si siguiéramos el criterio de Pizarro (1990) de utilizar como ETo de diseño el valor promedio mensual con 50 % de no excedencia, multiplicado por un factor de corrección de 1,2, los resultados obtenidos para las cinco estaciones serían: 6,8 – 7,0 – 6,1 – 7,3 – 6,4 mm d-1 respectivamente. Como se ve en el Cuadro 6, estos valores son prácticamente idénticos a los que se obtienen utilizando los valores diario con un 80 % de probabilidad de no excedencia.
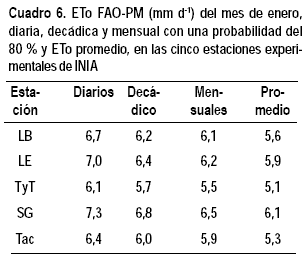
Galeazzi y Lutz (2008) encontraron que la ETo mensual con un 90 % de probabilidad de no excedencia era un 17 % mayor que la ETo mensual media. Con nuestros datos (valores no presentados), esa relación fue exactamente del 17 % en Las Brujas y Tacuarembó, 15 % en La Estanzuela, 14 % en Treinta y Tres y 9 % en Salto Grande.
La relación obtenida en nuestro caso entre la ETo mensual con un 75 % de probabilidad de no excedencia y la ETo mensual media varió entre un 6 y un 9 % en las diferentes zonas del país. En el Cuadro 7 se presentan los valores de ETo diaria con una probabilidad de no excedencia del 80 %, calculada con la Ecuación 3 (ETo 80 %) y el valor estimado con la Ecuación 1 (EToPn 80 %), asumiendo una distribución normal.
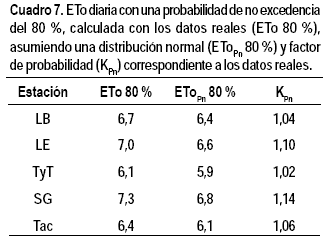
También se calculó el factor de probabilidad (KPn), despejando de la Ecuación 1 el valor del factor, para el valor de ETo diario correspondiente a un 80 % de probabilidad de no excedencia.
Se ve que los valores de ETo con una probabilidad del 80 % calculados a partir de los datos reales son en todos los casos superiores a los que se calcularían asumiendo una población con una distribución normal, con la misma media y la misma varianza. Esta asimetría se ve claramente en la Figura 1, y las causas fueron analizadas en el apartado correspondiente.
En la Figura 3 se presentan los valores mínimos y máximos para cada estación, calculados en períodos diarios, decádicos o mensuales. Se observa que los valores máximos absolutos registrados (Figura 3 – Diarios) rondan los 11 mm d-1 en Las Brujas, La Estanzuela y Salto Grande, 9 mm d-1 en Tacuarembó y poco más de 8 mm d-1 en Treinta y Tres. En contraste, los valores mínimos registrados en enero en las cinco estaciones no superan los 2 mm d-1.
Si los cálculos se hacen en períodos decádicos, en Salto Grande se observan valores de 10 mm d-1, mientras que en Las Brujas, La Estanzuela y Tacuarembó rondan los 7 mm d-1 y en Treinta y Tres apenas alcanza a 6,3 mm d-1. En este caso los valores mínimos rondan los 4 mm d-1.
Haciendo los cálculos con períodos mensuales, el valor máximo para SG es de 9 mm d-1 mientras que en las otras cuatro estaciones varía entre 6 y 7 mm d-1. Los valores mínimos varían entre 4 y 5 mm d-1.
De todo lo anterior se desprende que en el sur del país (Las Brujas y La Estanzuela) se pueden dar días con una ETo tan alta como en Salto Grande. Pero esa alta demanda atmosférica es sensiblemente menor en el sur que en Salto Grande si se toman períodos decádicos o mensuales. Dicho de otra forma, en Salto Grande las altas ETo se mantienen durante lapsos prolongados.
No se puede elaborar un mapa de isolíneas teniendo tan sólo los valores correspondientes a cinco puntos. Sin embargo, se dispone del mapa de isolíneas de ETo media de enero publicadas por INIA utilizando 24 estaciones climatológicas pertenecientes a la red de la Dirección Nacional de Meteorología y las cinco estaciones experimentales de INIA (Castaño et al., 2011).
Asumiendo que las isolíneas de ETo de enero, calculada en períodos decádicos con un 80 % de probabilidad y la ETo media de enero tienen la misma tendencia espacial, se elaboró el mapa que se muestra en la figura 4.
Se observa un gradiente de valores que aumenta de este a oeste. Esta distribución espacial se relaciona con un aumento de la radiación solar debido a la disminución de la nubosidad y disminución de la humedad relativa en el mismo sentido.
Este mapa permitirá la determinación de la ETo, como primer paso para el cálculo del diseño de los equipos de riego, en cualquier lugar del Uruguay.
Este valor, multiplicado por el coeficiente de cultivo (Kc) máximo para determinado cultivo, y corregido por la eficiencia de riego, determinará las necesidades brutas de riego (en mm d-1). Estas necesidades, multiplicadas por la superficie a regar (en m2) y dividido por el tiempo máximo que se va a regar por día (en horas) resultarán en el caudal de diseño del equipo de riego (en L h-1).
Un equipo así diseñado cubrirá la demanda total de agua del cultivo con una probabilidad del 80 %, o sea cuatro años de cada cinco.
Los equipos de riego se diseñan para regar no más de 20 horas por día. Sin embargo, en caso de demandas atmosféricas extraordinarias, pueden llegar a hacerse trabajar las 24 horas durante lapsos no muy prolongados. La forma en que influye ese aumento de la jornada de riego se analiza en el Cuadro 8.
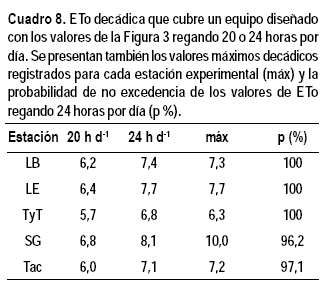
En resumen, un equipo diseñado a partir de los valores de ETo propuestos en este trabajo cubren la demanda de los cultivos con una probabilidad del 80 % (cuatro años de cada cinco) regando 20 horas por día. Pero aumentando dicha jornada de riego, con los mismos equipos, se cubren las máximas demandas históricas en Las Brujas, La Estanzuela y Treinta y Tres. En Salto Grande y Tacuarembó, los equipos así diseñados, aun regando 24 horas por día, no llegan a cubrir los máximos absolutos registrados, pero lo cubren con una probabilidad de no excedencia de 96 y 97 % respectivamente. Esto equivale a decir que solamente un año cada 25 o cada 33 el equipo no podrá cubrir la demanda promedio decádica.
Lo anterior no significa que dicho diseño será el de máxima rentabilidad, ya que para determinar la rentabilidad intervienen las funciones de respuesta de cada cultivo al agregado de agua, el precio del producto cosechado, los costos de inversión y operativos del equipo de riego.
Un equipo bien diseñado logra la mayor respuesta productiva del cultivo y tiene determinados costos fijos y variables. Debido a que la máxima respuesta productiva no se corresponde necesariamente con la máxima rentabilidad es necesario continuar con trabajos de investigación que permitan evaluar la respuesta productiva a distintas láminas máximas de reposición correspondientes a los diferentes caudales de diseño de los equipos de riego. Asimismo se deberá tener en cuenta que un equipo que aplique un menor caudal también tendrá menor costo fijo y variable.
Bibliografía
Allen RG, Wright JL, Pruitt WO, Pereira LS, Jensen ME. 2007. Water requirements. En: Hoffman GJ, Evans RG, Jensen ME, Martin DL, Elliot RL [Eds.]. Design and operation of farm irrigation systems. St. Joseph : A SABE. pp. 208 – 288.
Allen RG, Pereira LS, Raes D, Smith M. 1998. Crop evapotranspiration : Guidelines for computing crop water requirements. Rome : FAO. 300p. (FAO Irrigation and drainage paper ; 56).
Allen RG, Wright JL. 1983. Variation within the measured and estimated consumptive use requirements. En: Proceedings Specialty Conference on Advances in Irrigation and Drainage: Surviving External Pressures. Jackson Hole : ASCE. pp. 1 – 12.
Ávalos JL, Pacheco Seguí J. 2012. Programación del riego de la caña de azúcar en la provincia de Villa Clara, Cuba. Revista Ciencias Técnicas Agropecuarias, 21(4): 61 – 66.
Castaño JP, Giménez A, Ceroni M, Furest J, Aunchayna R. 2011. Caracterización agroclimática del Uruguay 1980-2009. Montevideo : INIA. 34p. (Serie Técnica ; 193).
Coolidge FL. 2012. Statistics : a gentle introduction. 3rd ed. Thousand Oaks : Sage Publications. 488p.
Doorenbos J, Pruitt WO. 1977. Crop water requirements. Rome : FAO, 200p. (FAO Irrigation and Drainage Paper ; 24).
Galeazzi J, Lutz C. 2008. Distribución de frecuencias de la evapotranspiración en el Alto Valle de Río Negro [En línea]. Neuquén : Facultad de Ciencias Agrarias. Universidad Nacional del Comahue. Consultado 6 de abril de 2014. Disponible en:http://agro.unc.edu.ar/~clima/AADA/Congresos/Jujuy/07_balance_de_agua/126%20-%20Galeazzi%20-%20Listo.pdf.
Pizarro F. 1990. Riegos localizados de alta frecuencia : Goteo, microaspersión, exudación. 2a ed. Madrid : Mundi-Prensa. 471p.
Puppo L, García Petillo M. 2010. Determinación del consumo de agua del duraznero por lisimetría. Revista Brasileira de Engenharia Agrícola e Ambiental, 14(1): 25 – 31.