Servicios Personalizados
Revista
Articulo
Links relacionados
Compartir
CLEI Electronic Journal
versión On-line ISSN 0717-5000
CLEIej vol.15 no.3 Montevideo dic. 2012
Abstract
This work presents parallel implementations of the MinMin scheduling heuristic for heterogeneous computing using Graphic Processing Units, in order to improve its computational efficiency. The experimental evaluation of the four proposed MinMin variants demonstrates that a significant reduction on the computing times can be attained, allowing to tackle large scheduling scenarios in reasonable execution times.
Spanish abstract:
Este trabajo presenta implementaciones paralelas de la heurística de planificiación MinMin para entornos de computación heterogénea usando unidades de procesamiento gráfico, con el fin de mejorar su eficiencia computacional. La evaluación experimental de las cuatro variantes propuestas para la heuristica MinMin demuestra que se puede alcanzar una reducción significativa en los tiempos de cálculo, lo que permite hacer frente a grandes escenarios de planificación en los tiempos de ejecución razonables.
Spanish keywords: computación en GPU, computación heterogénea, planificación.
Received: 2012-06-10 Revised 2012-10-01 Accepted 2012-10-04
In the last fifteen years, distributed computing environments have been increasingly used to solve complex problems. Nowadays, a common platform for distributed computing usually comprises a heterogeneous collection of computers. This class of infrastructures includes grid computing and cloud computing environments, where a large set of heterogeneous computers with diverse characteristics are combined to provide pervasive on demand and cost-effective processing power, software, and access to data, for solving many kinds of problems (1, 2).
A key problem when using such heterogeneous computing (HC) environments consists in finding a scheduling strategy for a set of tasks to be executed. The goal is to assign the computing resources by satisfying some efficiency criteria, usually related to the total execution time or resource utilization (3, 4). The heterogeneous computing scheduling problem (HCSP) became specially important due to the popularization of heterogeneous distributed computing systems (5, 6).
Traditional scheduling problems are NP-hard (7), thus classic exact methods are only useful for solving problem instances of very reduced size. Heuristics methods are able to get efficient schedules in reasonable times, but they still require long execution times when solving large instances of the scheduling problem. These execution times (i.e., in the order of an hour) can be extremely high for performing on-line scheduling in realistic HC infrastructures.
High performance computing techniques can be applied to reduce the execution times required to perform the scheduling. The massively parallel hardware in Graphic Processor Units (GPU) has been successfully applied to speed up the computations required to solve problems in many application areas (8), showing an excellent trade-off between cost and computing power (9).
The main contribution of this work is the development of four parallel implementations on GPU for a the classic and effective scheduling heuristic MinMin (10). The experimental evaluation of the proposed parallel methods demonstrates that a significant reduction on the computing times can be attained when using the parallel GPU hardware. This performance improvement allows solving large scheduling scenarios in reasonable execution times.
The manuscript is structured as follows. Next section introduces the HCSP mathematical formulation, and the heuristics studied in this work. A brief introduction to GPU computing is presented in Section 3. Section 4 describes the four proposed implementations of the MinMin heuristic on GPU. The experimental evaluation of the proposed methods is reported in Section 5, where the efficiency results are also analyzed. Finally, Section 6 summarizes the conclusions of the research and formulates the main lines for future work.
2 Heterogeneous computing scheduling
This section presents the HCSP and its mathematical formulation. It also provides a description of the class of list scheduling heuristics, and describes the MinMin method parallelized in this work.
An HC system is composed of many computers, also called processors or machines, and a set of tasks to be executed on the system. A task is the atomic unit of workload, so it cannot be divided into smaller chunks, nor interrupted after it is assigned to a machine. The execution times of any individual task vary from one machine to another, so there will be competition among tasks for using those machines able to execute them in the shortest time.
Scheduling problems mainly concern about time, trying to minimize the time spent to execute all tasks. The most usual metric to minimize in this model is the makespan, defined as the time spent from the moment when the first task begins execution to the moment when the last task is completed (4).
The following formulation presents the mathematical model for the HCSP aimed at minimizing the makespan:
- given an HC system composed of a set of machines
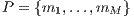 (dimension
(dimension 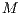 ), and a collection of tasks
), and a collection of tasks 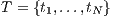 (dimension
(dimension 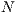 ) to be executed on the system,
) to be executed on the system, - let there be an execution time function
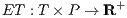 , where
, where 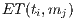 is the time required to execute the task
is the time required to execute the task 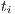 in the machine
in the machine 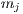 ,
, - the goal of the HCSP is to find an assignment of tasks to machines (a function
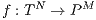 ) which minimizes the makespan, defined in Equation 1.
) which minimizes the makespan, defined in Equation 1. 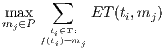
(1)
In the previous HCSP formulation all tasks can be independently executed, disregarding the execution order. This kind of applications frequently appears in many lines of scientific research, specially in Single-Program Multiple-Data applications used for multimedia processing, data mining, parallel domain decomposition of numerical models for physical phenomena, etc. The independent tasks model also arises when different users submit their (obviously independent) tasks to execute in grid computing and volunteer-based computing infrastructures -such as TeraGrid, WLCG, Berkeley’s BOINC, Xgrid, etc. (11)-, where non-dependent applications using domain decomposition are very often submitted for execution. Thus, the relevance of the HCSP version faced in this work is justified due to its significance in realistic distributed HC and grid environments.
2.2 List scheduling heuristics
The class of list scheduling heuristics comprises many deterministic scheduling methods that work by assigning priorities to tasks based on a particular criterion. After that, the list of tasks is sorted in decreasing priority and each task is assigned to a processor, regarding the task priority and the processor availability. Algorithm 1 presents the generic schema of a list scheduling method.
Since the pioneering work by Ibarra and Kim (12), where the first algorithms following the generic schema in Algorithm 1 were introduced, many list scheduling techniques have been proposed to provide easy methods for tasks-to-machines scheduling. This class of methods has also often been employed in hybrid algorithms, with the objective of improving the search of metaheuristic approaches for the HCSP and related scheduling problems.
The simplest list scheduling heuristics use a single criterion to perform the tasks-to-machines assignment. Among others, this category includes: Minimum Execution Time (MET), which considers the tasks sorted in an arbitrary order, and assigns them to the machine with lower ET for that task, regardless of the machine availability; Opportunistic Load Balancing (OLB), which considers the tasks sorted in an arbitrary order, and assigns them to the next machine that is expected to be available, regardless of the ET for each task on that machine; and Minimum Completion Time (MCT), which tries to combine the benefits of OLB and MET by considering the set of tasks sorted in an arbitrary order and assigning each task to the machine with the minimum CT for that task.
Trying to overcome the inefficacy of these simple heuristics, other methods with higher complexity have been proposed, by taking into account more complex and holistic criteria to perform the task mapping, and then reduce the makespan values. This work focuses on one of the most effective heuristics in this class:
- MinMin, which greedily picks the task that can be completed the soonest. The method starts with a set
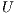 of all unmapped tasks, calculates the MCT for each task in
of all unmapped tasks, calculates the MCT for each task in  for each machine, and assigns the task with the minimum overall MCT to the best machine. The mapped task is removed from
for each machine, and assigns the task with the minimum overall MCT to the best machine. The mapped task is removed from 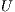 , and the process is repeated until all tasks are mapped. MinMin improves upon the MCT heuristic, since it does not consider a single task at a time but all the unmapped tasks sorted by MCT and by updating the machine availability for every assignment. This procedure leads to balanced schedules and also allows finding smaller makespan values than other heuristics, since more tasks are expected to be assigned to the machines that can complete them the earliest.
, and the process is repeated until all tasks are mapped. MinMin improves upon the MCT heuristic, since it does not consider a single task at a time but all the unmapped tasks sorted by MCT and by updating the machine availability for every assignment. This procedure leads to balanced schedules and also allows finding smaller makespan values than other heuristics, since more tasks are expected to be assigned to the machines that can complete them the earliest.
The computational complexity of MinMin heuristic is 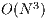 , where
, where 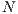 is the number of tasks to schedule. When solving large instances of the HCSP, large execution times are required to perform the task-to-machine assignment (i.e. several minutes for a problem instance with 10.000 tasks). In this context, parallel computing techniques can be applied to reduce the execution times required to find the schedules.
is the number of tasks to schedule. When solving large instances of the HCSP, large execution times are required to perform the task-to-machine assignment (i.e. several minutes for a problem instance with 10.000 tasks). In this context, parallel computing techniques can be applied to reduce the execution times required to find the schedules.
GPU computing has been used to parallelize many algorithms in diverse research areas. However, to the best of our knowledge, there have been no previous proposals of applying GPU parallelism to list scheduling heuristics.
GPUs were originally designed to exclusively perform the graphic processing in computers, allowing the Central Process Unit (CPU) to concentrate in the remaining computations. Nowadays, GPUs have a considerably large computing power, provided by hundreds of processing units with reasonable fast clock frequencies. In the last ten years, GPUs have been used as a powerful parallel hardware architecture to achieve efficiency in the execution of applications.
GPU programming and CUDA. Ten years ago, when GPUs were first used to perform general-purpose computation, they were programmed using low-level mechanism such as the interruption services of the BIOS, or by using graphic APIs such as OpenGL and DirectX (13). Later, the programs for GPU were developed in assembly language for each card model, and they had very limited portability. So, high-level languages were developed to fully exploit the capabilities of the GPUs. In 2007, NVIDIA introduced CUDA (14), a software architecture for managing the GPU as a parallel computing device without requiring to map the data and the computation into a graphic API.
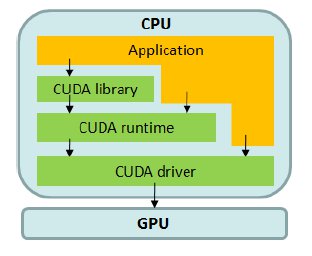
CUDA is based in an extension of the C language, and it is available for graphic cards GeForce 8 Series and superior. Three software layers are used in CUDA to communicate with the GPU (see Fig. 1): a low-level hardware driver that performs the CPU-GPU data communications, a high-level API, and a set of libraries such as CUBLAS for linear algebra and CUFFT for Fourier transforms.
For the CUDA programmer, the GPU is a computing device which is able to execute a large number of threads in parallel. A specific procedure to be executed many times over different data can be isolated in a GPU-function using many execution threads. The function is compiled using a specific set of instructions and the resulting program (named kernel) is loaded in the GPU. The GPU has its own DRAM, and the data are copied from the DRAM of the GPU to the RAM of the host (and viceversa) using optimized calls to the CUDA API.
The CUDA architecture is built around a scalable array of multiprocessors, each one of them having eight scalar processors, one multithreading unit, and a shared memory chip. The multiprocessors are able to create, manage, and execute parallel threads, with small overhead. The threads are grouped in blocks (with up to 512 threads), which are executed in a single multiprocessor, and the blocks are grouped into grids. When a CUDA program calls a grid to be executed in the GPU, each one of the blocks in the grid is numbered and distributed to an available multiprocessor. When a multiprocessor receives a block to execute, it splits the threads in warps, a set of 32 consecutive threads. Each warp executes a single instruction at a time, so the best efficiency is achieved when the 32 threads in the warp executes the same instruction. Each time that a block finishes its execution, a new block is assigned to the available multiprocessor.
The threads access the data using three memory spaces: a shared memory used by the threads in the block; the local memory of the thread; and the global memory of the GPU. Minimizing the access to the slower memory spaces (the local memory of the thread and the global memory of the GPU) is a very important feature to achieve efficiency. On the other hand, the shared memory is placed within the GPU chip, thus it provides a faster way to store the data.
4 MinMin implementations on GPU
The GPU architecture is better suited to the Single Instruction Multiple Data execution model for parallel programs. Thus, GPUs provide an ideal platform for executing parallel programs based on algorithms that use the domain decomposition strategy, especially when the algorithms execute the same set of instructions for each element of the domain.
The generic schema for a list scheduling heuristic presented in Algorithm 1 applies the following strategy: for each unassigneed task the criterial are evaluated on all machines and the task that best meets the criteria is selected and assigned to the machine which generates the minimum MCT. Clearly, this schema is an ideal case for applying a task-based or machine-based domain decomposition to generate parallel versions of the heuristics.
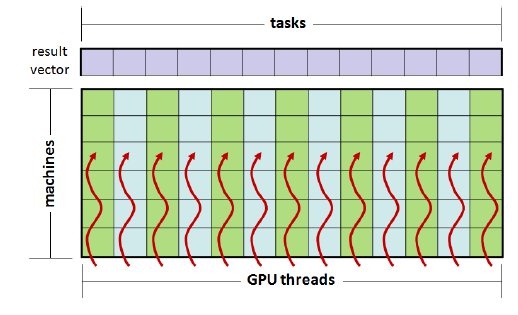
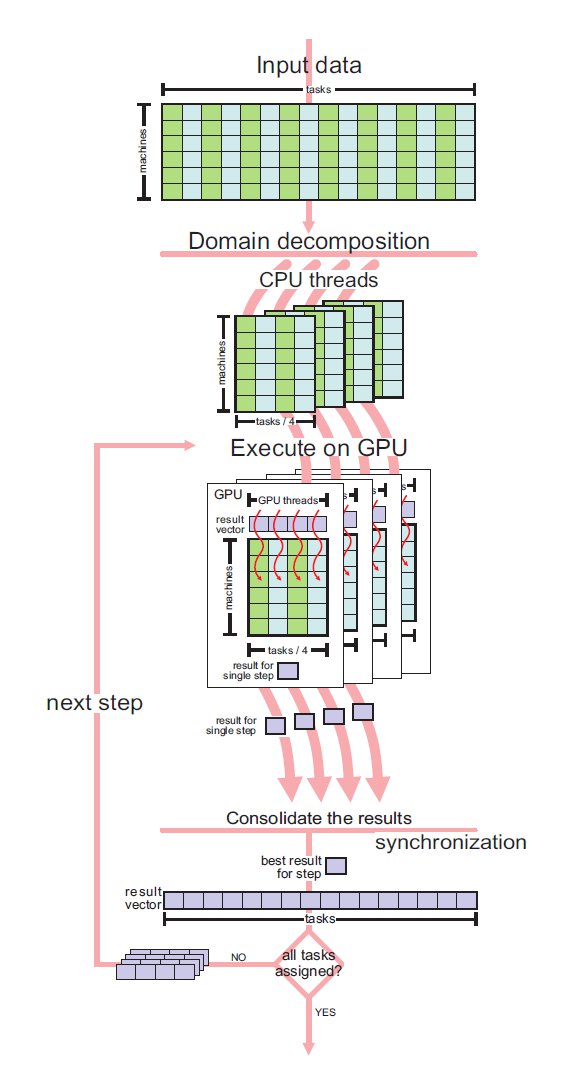
The four MinMin implementations on GPU designed in this work are based on the same generic parallel strategy. For each unassigned task, the evaluation of the criteria for all machines is performed in parallel on the GPU, building a vector that stores the identifier of the task, the best value obtained for the criteria, and the correspondent machine to get that value. The indicators in the vector are then processed in the reduction phase to obtain the best value that meets the criteria, and then the best pair (task, machine) is assigned. It is worth noting that the processing of the indicators to obtain the optimum value in each step is also performed using the GPU. A graphical summary of the generic parallel strategy applied in the parallel MinMin algorithms proposed in this article is presented in Fig. 2.
Four variants of the proposed MinMin implementation in GPU were designed:
- Parallel MinMin using one GPU (MinMin-1GPU), which executes on a single GPU, applying the aforementioned generic procedure;
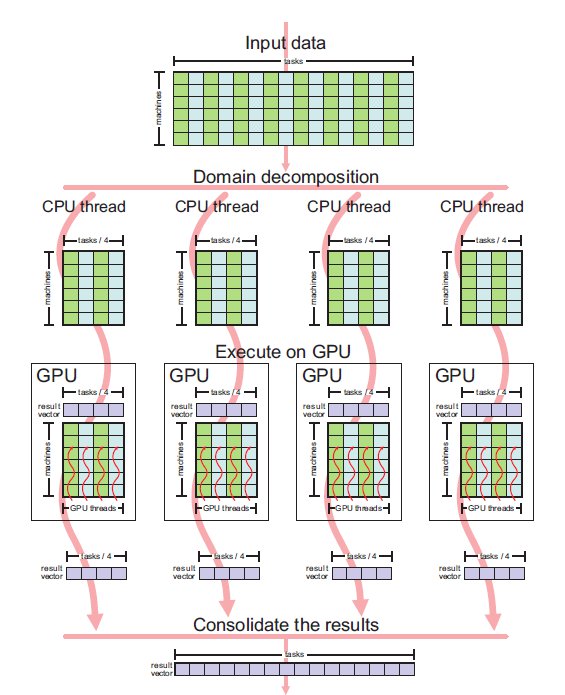
- Parallel MinMin in four GPUs with domain decomposition using pthreads (MinMin-4GPU-PT), which applies a master-slave multithreading programming approach implemented with POSIX threads (PThreads) that executes the same algorithm on four GPUs independently. The employed domain partition strategy splits the domain (i.e. the set of tasks) into
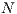 equally sized parts (being
equally sized parts (being 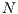 the number of GPUs used, four in our case), so that each task belongs to only one subset. Thus, each GPU performs the MinMin algorithm on a subset of the tasks input data on all machines, and a master process consolidate the results after each GPU finishes its task;
the number of GPUs used, four in our case), so that each task belongs to only one subset. Thus, each GPU performs the MinMin algorithm on a subset of the tasks input data on all machines, and a master process consolidate the results after each GPU finishes its task; - Parallel MinMin in four GPUs with domain decomposition using OpenMP (MinMin-4GPU-OMP), which applies the same master-slave strategy than the previous variant, but the multithreading programming is implemented using OpenMP. The only difference between this implementation and the previous variant lies in how the threads are handled, in this case they are automatically managed and synchronized using OpenMP directives included in the implementation. The code for loading input data, dumping the resulting data, performing the domain partition, and implementing the GPU kernel are identical to the one used in MinMin-4GPU-PT;
- Parallel synchronous MinMin in four GPUs and CPU (MinMin-4GPU-sync), which also applies a domain decomposition but it follows an hybrid approach. In each iteration, each GPU performs a single step of the MinMin algorithm, then a master process running in CPU assesses the result computed by each GPU and select the one that best meets the proposed criteria (i.e. MCT minimization), and finally the information of the selected assignment is updated in each GPU. This variant applies a multitheading approach implemented using pthreads to manage and synchronize the threads.
Figure 3 describes the parallel strategy used in the proposed implementations MinMin-4GPU-PT and MinMin-4GPU-OMP, where the CPU threads are defined and handled by using pthreads and OpenMP, respectively. Figure 4 describes the parallel strategy used in the synchronous implementation MinMin-4GPU-sync.
A specific data representation was used to accelerate the execution of the sequential implementation of the MinMin heuristic, in order to perform a fair comparison with the execution times of the GPU implementations. The sequential implementation use a data matrix (SoA) where each row represents a task and each column represents a machine. Thus, when performing the processing for tasks (rows), the entries are loaded to the cache of the processing core, allowing a faster way to access the data.
For parallel algorithms executing on GPU, loading the data matrix in the same way reduces the computational efficiency. Adjacent threads would access to the data stored in contiguous rows, but these are not stored contiguously, thus they cannot be stored in shared memory. When the data matrix is loaded so that each column represent a task and each row represent a machine, two adjacent threads in GPU access to the data stored in contiguous columns. These data are stored in contiguous memory locations, so they can be loaded in the shared memory, allowing to perform a faster data access for each thread, and therefore improving the execution of the parallel algorithm on GPU.
Preliminary experiments were also performed using a domain decomposition strategy that divides the data by machines rather than by tasks, but this option was finally discarded due to scalability issues as the problem size increases.
This section presents the experimental evaluation of the proposed MinMin implementations on GPU.
No standardized benchmarks or test suites for the HCSP have been proposed in the related literature (15). Researchers have often used the suite of twelve instances proposed by Braun et al. (16), following the expected time to compute (ETC) performance estimation model by Ali et al. (17).
ETC takes into account three key properties: machine heterogeneity, task heterogeneity, and consistency. Machine heterogeneity evaluates the variation of execution times for a given task across the HC resources, while task heterogeneity represents the variation of the tasks execution times for a given machine. Regarding the consistency property, in a consistent scenario, whenever a given machine 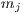 executes any task
executes any task 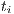 faster than other machine
faster than other machine 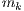 , then machine
, then machine 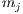 executes all tasks faster than machine
executes all tasks faster than machine 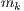 . In an inconsistent scenario a given machine
. In an inconsistent scenario a given machine 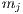 may be faster than machine
may be faster than machine 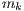 when executing some tasks and slower for others. Finally, a semi-consistent scenario models those inconsistent systems that include a consistent subsystem.
when executing some tasks and slower for others. Finally, a semi-consistent scenario models those inconsistent systems that include a consistent subsystem.
For the purpose of studying the efficiency of the GPU implementations as the problem instances grow, the experimental analysis consider a test suite of large-dimension HCSP instances, randomly generated to test the scalability of the proposed methods. This test suite was designed following the methodology by Ali et al. (17). The set includes the 96 medium-sized HCSP instances with dimension (tasks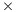 machines) 1024
machines) 1024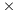 32, 2048
32, 2048 64, 4096
64, 4096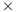 128 and 8192
128 and 8192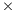 256 previously solved using an evolutionary algorithm (18), and new large dimension HCSP instances with dimensions 16384
256 previously solved using an evolutionary algorithm (18), and new large dimension HCSP instances with dimensions 16384 512, 32768
512, 32768 1024, 65536
1024, 65536 2048, and 131072
2048, and 131072 4096, specifically created to evaluate the GPU implementations presented in this work.
4096, specifically created to evaluate the GPU implementations presented in this work.
These dimensions are significanlty larger than those of the popular benchmark by Braun et al. (16) and they better model present distributed HC and grid systems. The problem instances and the generator program are publicly available to download at http://www.fing.edu.uy/inco/grupos/cecal/hpc/HCSP.
5.2 Development and execution platform
The parallel MinMin heuristics were implemented in C, using the standard stdlib library. The experimental analysis was performed on a Dell PowerEdge (QuadCore Xeon E5530 at 2.4 GHz, 48 GB RAM, 8 MB cache), with CentOS Linux 5.4 and four NVidia Tesla C1060 GPU (240 cores at 1.33 GHz, 4GB RAM) from the Cluster FING infrastructure, Facultad de Ingeniería, Universidad de la República, Uruguay (cluster website http://www.fing.edu.uy/cluster).
This section reports the results obtained when applying the parallel GPU implementations of the MinMin list scheduling heuristic for the HSCP instances tackled in this article.
In the experimental evaluation, we study two specific aspects of the proposed parallel MinMin implementations on GPU:
- Solution quality: The proposed parallel implementations modify the algorithmic behavior of the MinMin heuristic, so the makespan results obtained with the GPU implementations are not the same than those obtained with the sequential versions for the studied HCSP instances. We evaluate the relative gap with respect to the traditional (sequential) MinMin for each method, as defined by Eq. 2, where
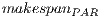 and
and 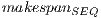 are the makespan values computed using the parallel and the sequential MinMin implementation, respectively.
are the makespan values computed using the parallel and the sequential MinMin implementation, respectively. 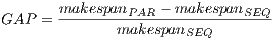
(2)
- Execution times and speedup: We analyze the wall-clock execution times and the speedup for each parallel MinMin implementation with respect to the sequential one. The speedup metric evaluates how much faster a parallel algorithm is than its corresponding sequential version. It is computed as the ratio of the execution times of the sequential algorithm (
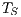 ) and the parallel version executed on
) and the parallel version executed on 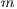 computing elements (
computing elements (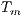 ) (Equation 3). The ideal case for a parallel algorithm is to achieve linear speedup (
) (Equation 3). The ideal case for a parallel algorithm is to achieve linear speedup (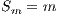 ), but the most common situation is to achieve sublinear speedup (
), but the most common situation is to achieve sublinear speedup ( ), mainly due to the times required to communicate and synchronize the parallel processes. However, when using GPU infrastructures very large speedup values have been often reported.
), mainly due to the times required to communicate and synchronize the parallel processes. However, when using GPU infrastructures very large speedup values have been often reported. 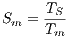
(3)
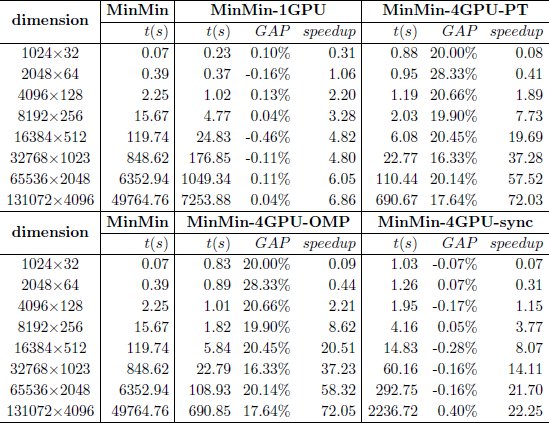
Table 1 reports the average execution times (in seconds), the average GAP values and the average speedup for each of the four parallel MinMin implementations on GPU studied, and a comparison with the sequential implementation in CPU. The results in Table 1 correspond to the average values for all the HCSP instances solved for each problem dimension studied, and the comparison is performed considering the optimized sequential algorithms using the specialized data representation described in Section 4.
The results in Table 1 show that significant improvements on the execution times of MinMin are obtained when using the GPU implementations for problem instances with more than 8.000 tasks. When solving the low-dimension problem instances, the GPU implementations were unable to outperform the execution times of the sequential MinMin, mainly due to the overhead introduced by the threads creation and management, and the CPU-GPU memory movements. However, when solving larger problem instances that model realistic large grid scenarios, significant improvements in the execution times are achieved, specially for the problem instances with dimension 65536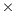 2048 and 131072
2048 and 131072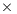 4096.
4096.
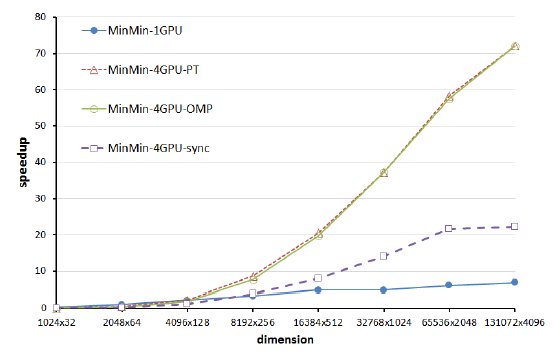
Regarding the computational efficiency, Fig. 5 summarizes the speedup values for the GPU implementations for each problem dimension faced.
The evolution of the speedup values in Fig. 5 indicates that the four GPU implementations obtained small accelerations for the HCSP instances with dimension less than 8192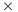 256. However, as the dimension of the problem instances grow (16384
256. However, as the dimension of the problem instances grow (16384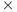 512, 32768
512, 32768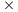 1024, 65536
1024, 65536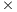 2048, and 131072
2048, and 131072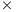 4096), reasonable speedup values are obtained for the parallel implementations. The best speedup values were computed for the two largest problem dimensions, with a maximum of 72.05 for the parallel asynchronous MinMin implementation on four GPUs using OpenMP threads.
4096), reasonable speedup values are obtained for the parallel implementations. The best speedup values were computed for the two largest problem dimensions, with a maximum of 72.05 for the parallel asynchronous MinMin implementation on four GPUs using OpenMP threads.
The four studied MinMin variants in GPU provide different trade-off values between the quality of solutions and execution time required. The asynchronous implementations applying domain decomposition using four GPUs (MinMin-4GPU-PT and MinMin-4GPU-OMP) have the largest speedup values, but the results quality are from 16% to 20% worst than the sequential MinMin implementation. Despite the aforementioned reductions in the solution quality, these methods are able to compute the solutions in reduced execution times (i.e. about 10 minutes in the larges scenario studied, when scheduling 131072 tasks on 4096 machines), thus they can be useful to rapidly solve large scheduling scenarios. On the other hand, the parallel synchronous version of MinMin using four GPUs computed exactly the same solution than the sequential MinMin, but it improves the execution time in a factor of up to 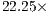 for the largest instances tackled in this work.
for the largest instances tackled in this work.
The previously commented results indicate that the proposed parallel implementation of the MinMin list scheduling heuristic in GPU are accurate and efficient methods for scheduling in large HC and grid infrastructures. All parallel variants provides promising reductions in the execution times when solving large instances of the scheduling problem.
This article studied the development of parallel implementations in GPU for a weel-known effective list scheduling heuristic algorithm, namely MinMin, for scheduling in heterogeneous computing environments.
The four proposed algorithms were developed using CUDA, following a simple domain decomposition approach that allows scaling up to solve very large dimension problem instances. The experimental evaluation solved HCSP instances with up to 131072 tasks and 4096 machines, a dimension far more larger than the previously tackled in the related literature.
The experimental results demonstrated that the parallel implementations of MinMin on GPU provide significant accelerations over the time required by the sequential implementations when solving large instances of the HCSP. On the one hand, the speedup values raised up to a maximum of 72.05 for the parallel asynchronous MinMin implementation on four GPUs using OpenMP threads. On the other hand, the parallel synchronous version of MinMin using four GPUs computed exactly the same solution than the sequential MinMin, but improving the execution time in a factor of up to 22.25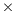 for the largest instances tackled in this work.
for the largest instances tackled in this work.
The previously commented results demonstrate that the parallel MinMin implementations in GPU introduced in this article are accurate and efficient schedulers for HC systems, which allow tackling large scheduling scenarios in reasonable execution times.
The main line for future work is related with improving the proposed GPU implementations, mainly by studying the management of the memory accessed by the threads. In this way, the computational efficiency of the heuristics on GPU can be further improved, allowing to develop even more efficient parallel implementations. Another line for future works is used this implementations for complement the efficient heuristic local search methods implemented on GPU. We are working on these topics right now.
(1) I. Foster and C. Kesselman, The Grid: Blueprint for a Future Computing Infrastructure. Morgan Kaufmann Publishers, 1998.
(2) T. Velte, A. Velte, and R. Elsenpeter, Cloud Computing, A Practical Approach. New York, NY, USA: McGraw-Hill, Inc., 2010.
(3) H. El-Rewini, T. Lewis, and H. Ali, Task scheduling in parallel and distributed systems. Prentice-Hall, Inc., 1994.
(4) J. Leung, L. Kelly, and J. Anderson, Handbook of Scheduling: Algorithms, Models, and Performance Analysis. CRC Press, Inc., 2004.
(5) M. Eshaghian, Heterogeneous Computing. Artech House, 1996.
(6) R. Freund, V. Sunderam, A. Gottlieb, K. Hwang, and S. Sahni, “Special issue on heterogeneous processing,” J. Parallel Distrib. Comput., vol. 21, no. 3, 1994.
(7) M. Garey and D. Johnson, Computers and intractability. Freeman, 1979.
(8) D. Kirk and W. Hwu, Programming Massively Parallel Processors: A Hands-on Approach. Morgan Kaufmann, 2010.
(9) J. Owens, M. Houston, D. Luebke, S. Green, J. Stone, and J. Phillips, “GPU computing,” Proceedings of the IEEE, vol. 96, no. 5, pp. 879–899, May 2008.
(10) Y. Kwok and I. Ahmad, “Static scheduling algorithms for allocating directed task graphs to multiprocessors,” ACM Comput. Surv., vol. 31, no. 4, pp. 406–471, 1999.
(11) F. Berman, G. Fox, and A. Hey, Grid Computing: Making the Global Infrastructure a Reality. New York, NY, USA: John Wiley & Sons, Inc., 2003.
(12) O. Ibarra and C. Kim, “Heuristic algorithms for scheduling independent tasks on nonidentical processors,” Journal of the ACM, vol. 24, no. 2, pp. 280–289, 1977.
(13) R. Fernando, Ed., GPU gems. Boston: Addision-Wesley, 2004.
(14) nVidia, “CUDA website,” Available online http://www.nvidia.com/object/cuda_home.html, 2010, accessed on July 2011.
(15) M. Theys, T. Braun, H. Siegel, A. Maciejewski, and Y. Kwok, “Mapping tasks onto distributed heterogeneous computing systems using a genetic algorithm approach,” in Solutions to parallel and distributed computing problems. New York, USA: Wiley, 2001, pp. 135–178.
(16) T. Braun, H. Siegel, N. Beck, L. Bölöni, M. Maheswaran, A. Reuther, J. Robertson, M. Theys, B. Yao, D. Hensgen, and R. Freund, “A comparison of eleven static heuristics for mapping a class of independent tasks onto heterogeneous distributed computing systems,” J. Parallel Distrib. Comput., vol. 61, no. 6, pp. 810–837, 2001.
(17) S. Ali, H. Siegel, M. Maheswaran, S. Ali, and D. Hensgen, “Task execution time modeling for heterogeneous computing systems,” in Proc. of the 9th Heterogeneous Computing Workshop, Washington, USA, 2000, p. 185.
(18) S. Nesmachnow, “A cellular multiobjective evolutionary algorithm for efficient heterogeneous computing scheduling,” in EVOLVE 2011, A bridge between Probability, Set Oriented Numerics and Evolutionary Computation, 2011.