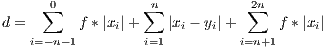Serviços Personalizados
Journal
Artigo
Links relacionados
Compartilhar
CLEI Electronic Journal
versão On-line ISSN 0717-5000
CLEIej vol.14 no.3 Montevideo dez. 2011
Abstract
GAVIS (Genetic Algorithm based Voice Imitation System), [1], is a system whose purpose is to find a set of effects to imitate voice signals. The system is based on Genetic Algorithms and Fourier Transforms. Although GAVIS proves to be effective, some deficiencies were found, and amongst them was the execution speed of the system. It is to improve such deficiencies that a new version of the system was designed and implemented. In this paper, we present the foundations for GAVIS’ construction and a new and improved design and implementation of GAVIS (J-GAVIS) and describe its new features.
GAVIS (Genetic Algorithm based Voice Imitation System) es un sistema cuyo propósito es de encontrar un conjunto de efectos de sonido para lograr imitación de señales de voz. El sistema está basado en Algoritmos Genéticos y Transformadas de Fourier. Si bien la versión original de GAVIS era efectiva, se encontraron algunas deficiencias. Una de ellas era la velocidad de ejecución del sistema. Se diseñó e implementó una nueva versión del sistema para mejorar las deficiencias encontradas en la versión anterior. En este artículo, se presentan los fundamentos de la construcción de GAVIS, el diseño e implementación mejoradas de la nueva versión (J-GAVIS) y se describen además las nuevas características presentes en J-GAVIS.
Keywords: Heuristics, Voice Imitation, Genetic Algorithms, Fourier Transform, Speech Processing.
Keywords: Heurísticas, Imitación de voz, Algoritmos Genéticos, Transformada de Fourier, Procesamiento de voz.
Received: 2011-03-30 Revised: 2011-10-06 Accepted: 2011-10-06
Speech recognition and speech processing are subjects that are actively researched nowadays and that are intimately related to the use of voice signals. These topics yield several problems. One of them is the imitation of a target voice by means of audio effects and constitutes the main focus of this article, specifically, finding the mentioned effects that transform a phoneme emitted by a source voice into the same phoneme emitted by a target voice.
Solving the problem has several practical applications, for example: It can be used to dub films as to turn the voice of the dubbing actor into the voice of the original actor. It can also be used in advertising, if the voice of a specific person is needed but this person is unavailable.
Voice signals were used for several calculations and the Discrete Fourier Transform (from now on known as DFT) was key in offering a representation to manipulate easily such signals. Actually, most of the operations applied on a signal were done through the DFT.
Presently, there are systems capable of solving this problem. Therefore, our proposal aims to improve the quality of the results obtained by said existing systems [2], [1].
Multidimensionality of the problem and high variety of solutions in the search space led to the selection of Genetic Algorithms to perform the task. Also, the fact that the expected result is known and that a solution can always be accurately assessed reinforces this choice. Some non-conventional elements which will be discussed have also been added to the Genetic Algorithm as to further aid in the search.
The problem of transforming a voice signal into another has a trivial solution. Nonetheless, finding a set of effects which can approximate the DFT of two or more input signals to their respective output signal DFTs is not an easy task.
The work here presented consists in a description of the implementation of a model that uses heuristic search methods to find the audio effects needed for the aforementioned transformation and its subsequent improvement.
In section 2, a brief overview of Genetic Algorithms will be given. Section 3 will describe some relevant notions on Audio Signals and DFTs. Section 4 describes the design and implementation of the original GAVIS. Section 5 will discuss the deficiencies found in GAVIS and the necessity of a new version along with the new system’s design and the implementation of all its relevant features. In section 6, results will be presented, analyzed and compared to the results of the previous version. Finally, we conclude in section 7 and sketch current and future work.
Genetic algorithms are a heuristic search technique mainly used for optimizing solutions (i.e. Combinatorial Optimization) to a problem [3], [4]. It is strongly based on species evolution. The idea behind the operation of the algorithm is that of the use of several initial solutions and evolving them by evaluating their overall quality and applying genetic operators to make them gradually improve. Although this type of algorithms is good at approximating optimal solutions, it never guarantees to find the optimal solution.
Generally, solutions are coded as arrays of values (chromosomes) composed by features of such solutions. Each feature (gene) may be represented as binary numbers or as another data type. This constitutes the valid language for the phenotype or individual, which is an embodiment of a particular potential solution for the problem to be solved.
A brief description for each element involved in the algorithm will be given.
The phenotype is the representation of an individual solution within the search space. It serves as a model for potential solutions to the problem. It may also be referred to as individual.
A chromosome is an encoding for the phenotype. It is typically a string, although it might have other forms such as graphs, matrices or any data structure depending on the problem to be solved.
Pool of individuals used for evolving. As a result of the change in the solutions of the pool, the population itself naturally changes. Each step (iteration) in this process is called generation, and constitutes an epoch or a snapshot of the population at a certain time in the execution.
The fitness function evaluates the quality of a given individual. It is commonly used to test the stopping criterion and to pair the individuals in the population who will undergo crossover.
It is a genetic operator that combines individuals and produces offspring solutions that preserve several features of the original individuals.
It is another genetic operator that applies a spontaneous change to a given offspring solution. The main goal of this operator is to maintain a minimum of diversity for exhaustive exploration of the search space.
The natural selection criterion is the one for eliminating unfit individuals along the execution of the algorithm. The implementation of this operation usually holds a close relationship with the fitness function, but may also be defined in a different manner.
A criterion that must be met to end the execution of the algorithm. Generally, this criterion might be associated to the quality of the best solution, convergence of the population, fixed number of iterations or a combination of the mentioned criteria.
Some parameters are needed for the Genetic Algorithm to be fully defined such as Population size, Crossover probability 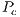 , Mutation probability
, Mutation probability 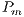 among others.
among others.
A psuedocode for a Genetic Algorithm is as follows:
- Initial population creation (usually random)
- Evaluation of each individual in the population
- While the termination criterion is not met
- Apply crossover with probability
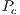 to a certain subset of the population
to a certain subset of the population - Apply mutation with probability
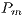 to each generated offspring solution
to each generated offspring solution - Evaluation of each individual in the population
- Verify natural selection criterion on all the individuals in the population and apply elimination when needed
- Repopulate with new individuals if needed to meet population size
- Apply crossover with probability
- Return the best solution found
A DFT is a tool that allows the visualization of a signal in the frequency domain [5], [6], [7], and it is defined as:
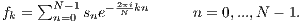
where:
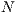 is the number of samples of the signal.
is the number of samples of the signal. 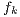 is the
is the 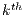 component of the array that represents the DFT.
component of the array that represents the DFT. 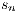 is the
is the 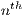 component of the input signal expressed in the time domain.
component of the input signal expressed in the time domain.
It must be noted that each 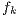 and each
and each 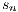 is a complex number. The reason for using a DFT is that the alterations made on an array represent a sound effect if the array is a DFT. If the array represented a signal in the time domain, said alterations would result in meaningless distortion and misplacement of the sound waves, which is not a useful reconfiguration of the signal.
is a complex number. The reason for using a DFT is that the alterations made on an array represent a sound effect if the array is a DFT. If the array represented a signal in the time domain, said alterations would result in meaningless distortion and misplacement of the sound waves, which is not a useful reconfiguration of the signal.
4 The original GAVIS - Design and Implementation
The system was originally designed to find a set of sound effects needed to convert one voice into another. It was found that the core of the problem is that of an array converter. The idea of the system is to find a set of changes such that when they are applied to source values, a good approximation of the target values is obtained. These changes use sections of the array. Basically, a random section of the array is chosen and then the values in that section are added to the values in another area of the array.
More specifically, the mentioned changes are based on three concepts:
- Initial section: Has start and end index that define a portion of the array.
- Destination section: Is defined by a starting index where the initial section will be added. This area is selected randomly, but it must fit within the boundaries of the array. The following image shows how the initial section is added to the destination section:
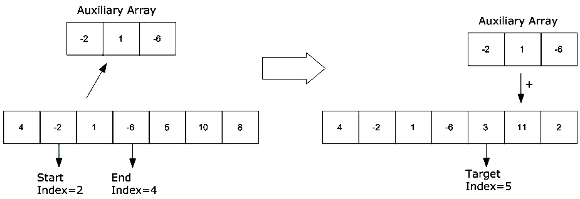
- Coefficients: The initial section, destination section and/or the values that will be added are multiplied by a certain factor.
These changes are actually also sound effects that generate some transformation when they are applied to the DFT of a sound signal. It is to be noted that any number of said effects may be used on the DFT of any signal. This is done by processing each transformation sequentially, which means that each effect makes its own changes on the DFT of a signal that has already undergone changes due to the processing of all previous effects.
In this version of the system, an individual is partly composed by an array of chromosomes. Each chromosome contains several parameters that describe a sound effect as it was proposed. This poses a problem, in the sense that all the values are linked and a change in one of them may produce an invalid chromosome. The corresponding mutation operator addresses this problem, and it will be described later in this section.
The chromosome’s parameters will be briefly named and explained:
- Left limit: It is a random integer value between the initial and final indices of the array.
- Right limit: It is generated in the same way than left limit, but if its value is lower than left limit’s, they are swapped. Both left limit and right limit are the boundaries of the initial section.
- Target: Is a randomly generated integer value that will act as the starting point for the destination section.
- Initial section coefficient: The factor by which the initial section is multiplied.
- Destination section coefficient: Coefficient that multiplies the destination section.
- Added section coefficient: The initial section is stored in an auxiliary array, this array is then multiplied by the added section coefficient and furthermore added to the destination section. To generate all three mentioned coefficients, the first step is to generate a random boolean value to determine whether the coefficient should be a number between 0 and 1 or whether it should be a number between 1 and a given maximum coefficient value. Next step is to generate another random boolean value that will decide if the overall value of the coefficient will be multiplied by -1 or not.
The reasons behind the steps used to generate the coefficients in the chromosome, are that negative coefficients may be needed, and to avoid a bias in the population by having a greater chance of obtaining a coefficient that multiplies than one that divides.
Other than the chromosomes, an individual has variables that store the fitness and age.
In order to obtain the fitness of an individual, the effects in the chromosomes are sequentially applied to the DFT of the source signal and then a Euclidean distance  is calculated between the resulting array and the array that represents the DFT of the target signal. This process is summarized in the following equation:
is calculated between the resulting array and the array that represents the DFT of the target signal. This process is summarized in the following equation:
where:
 is the Euclidean distance
is the Euclidean distance 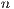 is the number of chromosomes assigned to the individual
is the number of chromosomes assigned to the individual 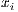 is the
is the 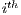 component of the array
component of the array 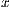 , being
, being 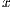 the original array with all the effects applied to it
the original array with all the effects applied to it 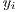 is the
is the 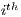 component of the array
component of the array 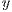 , being
, being 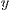 the target array
the target array
A feature to be noted is the use of a lifespan (age) variable for individuals. This lifespan is measured in terms of iterations of the main algorithm. The variable is used to eliminate “old” individuals, being the purpose to restrict excessive dissemination of a good individual’s characteristics to avoid premature convergence. When an individual “dies” from age, it is replaced by a new randomly generated individual.
The two main genetic operators, crossover and mutation, are present in this implementation of the system and are defined as follows:
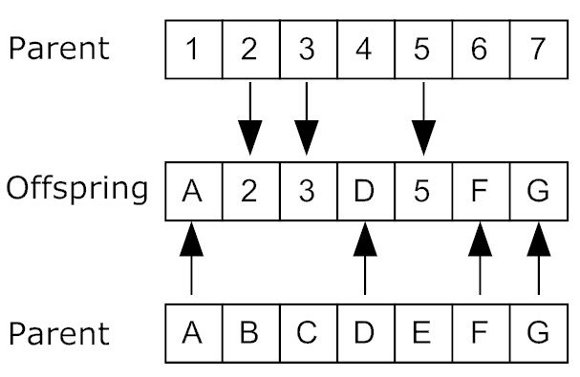
- Crossover: Selects the individuals to be combined and generates a single new individual. The offspring individual inherits a chromosome
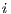 from one of its parent individuals. The source of the chromosome is decided by a boolean random number. It is important to note that the location of the inherited chromosome is the same in the offspring individual. Figure 1 shows the process on a couple of random arrays.
from one of its parent individuals. The source of the chromosome is decided by a boolean random number. It is important to note that the location of the inherited chromosome is the same in the offspring individual. Figure 1 shows the process on a couple of random arrays.
The phenotypes are initially sorted by their fitness value. Then, for each phenotype in the population a companion is chosen using a “crossover distance” which is described by the following equations:
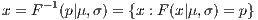
(1)
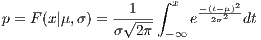
(2)
where (1) represents a normal inverse cumulative distribution function, and (2) denotes
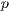 .
. 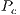 is 1 under this implementation.
is 1 under this implementation.
- Mutation: Applies a random transformation on one or more of the parameters of a given chromosome. If the transformation affects left limit and/or right limit, target must be recalculated. The values produced by the transformation are obtained in the same manner that the initial values of the individual were generated. In this case, the mutation’s objective is to un-link the parameters inside a chromosome and to diversify the population. Mutation is activated with probability
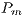 when offspring is spawned from crossover.
when offspring is spawned from crossover.
Due to crossover, each iteration doubles the size of the population. Therefore, to maintain a fixed population size, the offspring is evaluated, then the population is sorted again by its fitness and the worst half of the population is discarded. This operation constitutes Natural Selection simulation for the implementation.
Also, this implementation stops when a certain number of iterations was completed. It stores a copy of the best individual found across all generations.
This version of the system was implemented in Matlab R2010b [8].
R2010b [8].
Having completed the implementation and testing on GAVIS, some defects were found:
- The system’s execution speed was really slow.
- Convergence took a very long time.
- Although the obtained solution was good, better solutions could be obtained.
We sought to address these deficiencies by the following means:
- Changing the programming language.
- Redefining some of the elements in the system.
The change in the programming language was of great aid. We chose Java as the new language for implementation due to its portability and ready-to-use functionalities. Another factor which favored the election of Java as the new language was its comparative speed of execution compared to Matlab. In the next section, some comparative results between both versions will be shown.
As far as the redefinition of elements in the algorithm, we could identify a couple of key elements which needed to be redesigned. In this section, we shall describe and explain both of the elements which were redesigned.
First of all, we redesigned the representation of a change in the signal. This was due to the fact that a change had to be more versatile than a section of the array. We found that transporting sections of the array made the combination spectrum way too wide since the search needed to find the adequate size of the section and also the adequate section. Therefore, the new structure of a change is as follows:
- Initial index: Refers to a specific value in the array at a certain index. This value ranges from
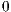 to
to 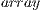
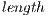 .
. - Offset: Defines a distance from the initial index. It must be noted that offset may have values in the range
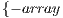
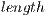 ,
, 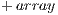
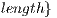 .
. - Destination index: It is the number where initial index will be transported as to be added. The value is determined by initial index + offset. This value may be outside of the array’s boundaries.
- Gain: The value that will be added is multiplied by this coefficient.
The following figure shows the process in which a change is made on an array under the new implementation:
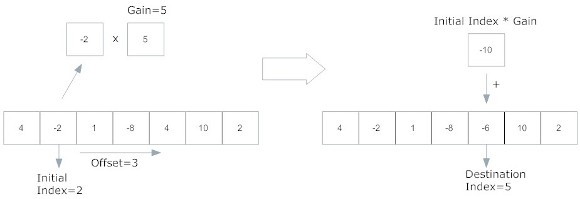
As in the previous version of the system, the changes are actually also sound effects that generate some transformation when they are applied to the DFT of a sound signal. Also, the application of the changes is still cumulative.
The new version of the changes were created in order to lower the number of operations performed by a gene within each individual. This new approach achieves a more fine-grained evolution on each individual and yields a “high definition” individual.
This choice allows a greater freedom when crossover is executed since the new individuals have more elements than in the original version, leading to a greater number of possible crossover points.
An individual under the new implementation here presented is still defined as being partly composed by an array of chromosomes. However, it was greatly simplified from the previous version.
As in the former version of the system, an individual has variables that store the fitness and an age.
It is to be noted that under this implementation of the system, the mutation operator is now irrelevant due to the number of new genes that enter the population by means of the process mentioned above.
The original fitness function of an individual was modified to penalize changes that occur outside of the boundaries of the array. Nonetheless, the main concept of the function was preserved and still refers to a total Euclidean distance 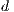 between the array with the effects already applied on it and the array representing the DFT of the target signal. The following equation shows how the value is calculated:
between the array with the effects already applied on it and the array representing the DFT of the target signal. The following equation shows how the value is calculated:
where:
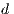 is the Euclidean distance
is the Euclidean distance 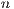 is the number of chromosomes assigned to the individual
is the number of chromosomes assigned to the individual 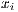 is the
is the 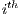 component of the array
component of the array 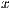 , being
, being 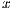 the original array with all the effects applied to it
the original array with all the effects applied to it 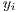 is the
is the 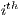 component of the array
component of the array 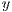 , being
, being 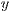 the target array
the target array 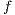 is a scalar factor used as a coefficient for penalty
is a scalar factor used as a coefficient for penalty
It may be observed in (3) that 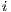 may have values lower than 1 and greater than
may have values lower than 1 and greater than 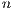 . The reason for using the values outside the boundaries of the array is for the algorithm to learn proper values for the offset parameter and to randomly nullify certain changes.
. The reason for using the values outside the boundaries of the array is for the algorithm to learn proper values for the offset parameter and to randomly nullify certain changes.
The Natural Selection simulation model was preserved from the previous version. Nonetheless, some alternatives were tested before making this choice:
- Eliminating a uniformly distributed group of individuals.
- Maintaining only the offspring individuals (crossover was different and two new solutions were spawned instead of one).
Neither of these alternatives proved to be better than eliminating the worst half of the population. Also it is to be emphasized that the age helped to keep the diversity in the population across all iterations since it forces new individuals to replace old ones.
Several results were obtained from tests executed on the system. The instances of the tests all included two input arrays and two destination arrays. Each execution used the following parameters:
- Signal length: 15 samples
- Number of chromosomes per individual: 300
- Population size: 1000
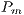 : 0.5
: 0.5 - Probability of changing a parameter of a chromosome: 0.05
- Individual lifespan: 5 generations
- Iterations: 1500
These tests were performed on both the previous and the current implementation with the same parameters to make the comparison as fair as possible.
The results of the tests are shown in Figures 2 (for GAVIS) and 3 (for J-GAVIS).
These results show that J-GAVIS’ performance is clearly superior to that of GAVIS.
These improvements can be explained due to the following reasons:
- The better results in quality of the solution may be explained by the new structure of the changes that are being used in the new implementation. As mentioned previously, the changes now target single element in the array, instead of a full section of the array. By operating in this manner, greater precision is achieved since changing a single element in the array yields a lower impact variation whereas using a whole section of the array for the change has a higher impact. Hence, two positive effects may be observed when using the new embodiment of the changes:
- More subtle transformations are achieved by using only one of the components of the array. The solutions that are obtained are more fine-grained.
- Using a section of an array to implement transformations has the risk of changing a vicinity of the component which needed to be improved. Potentially, this vicinity had high quality but was being overwritten or modified by the incoming section. Using a single component of the array to represent the change eliminates this “collateral damage”.
- Improvement in speed can be observed in the performance charts shown in this section. We explain this improvement due to the fact that MATLAB is natively an interpreted language, which makes it execute slower than Java which is not. Another of the reasons why J-GAVIS executed faster than the original GAVIS, is that we found a deficiency in the evaluation process in GAVIS, happening twice in the case of certain individuals, since under the original implementation it was not possible to know when an individual had been freshly evaluated or not. We also found that eliminating the mutation operator (it was not necessary under the new version) did help to make the speed faster.
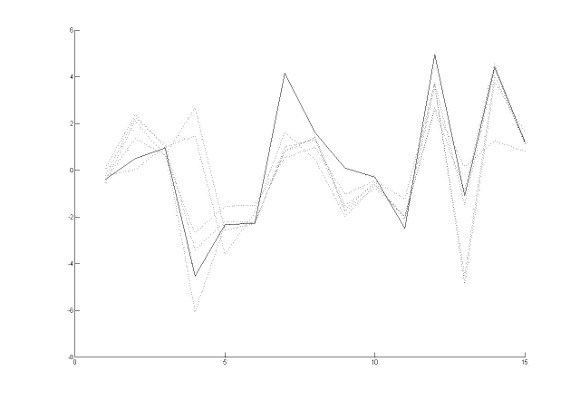
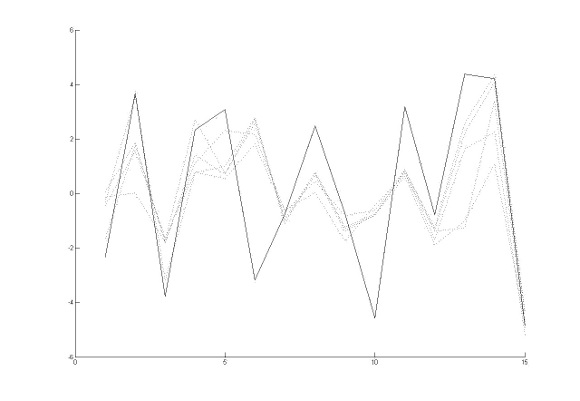
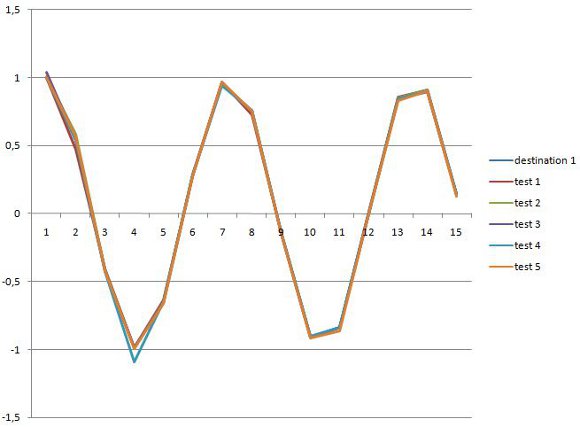
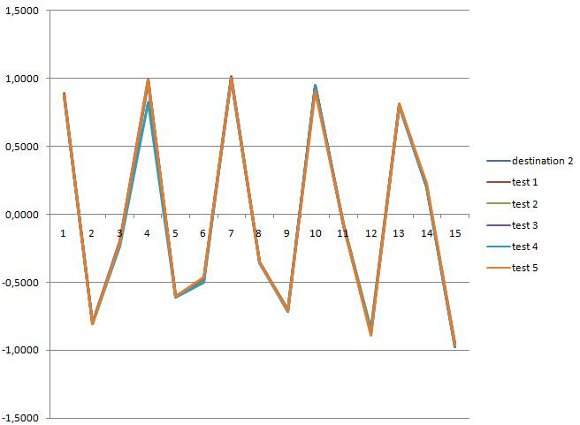
Figures 4 and 5 show the two output arrays for GAVIS and the found solutions. Figures 6 and 7 show the two output arrays for J-GAVIS and the respective solutions. In Figures 4 and 5, the dotted lines represent each transformation of the respective original arrays using the effect described by the best individual found at each test. The solid line in the same Figures denotes the target array. For figures 6 and 7 each color line represents a test and the cyan colored line represents the target signal.
Again, it may be noted that the results obtained for J-GAVIS are of greater quality than those obtained by GAVIS.
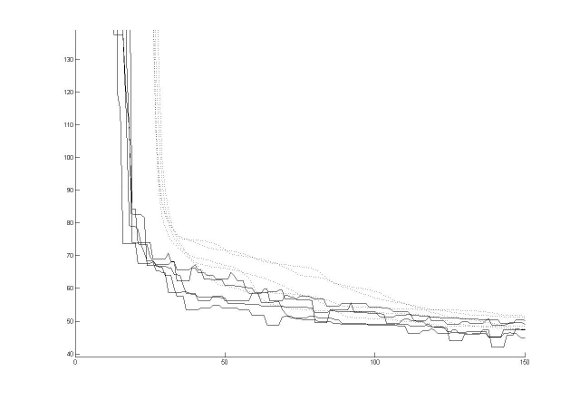
In figure 8 the dotted line symbolizes the average of the distance for all the population at each generation. The solid line in the same Figure shows the evaluation (distance) of the best individual at each generation.
It may be observed that for the first generations of the execution, the distance diminishes in a greater ratio than at later generations. Also, the difference between the fitness of the best individual and the average fitness of the population is also greater toward early generations. This pattern was present in both GAVIS and J-GAVIS.
It must be noted that at certain generations, the fitness of the best individual is worse than that of the best individual at a previous generation. This is due to the fact that a better individual did not spawn from the current generation and that the former best individual died of age.
The average fitness of the population has a tendency to improve over all generations. This implies that all the population gradually lowers its distance. This tendency was observed in both implementations of the system.
7 Conclusions, current and future work
In this work, it has been empirically shown that it is possible to obtain a set of effects such that when it is applied to multiple source signal DFT arrays, the result approximates the corresponding target signal DFT arrays. Based on these results, a conclusion that may be inferred is that using multiple samples of source and target voices, it is possible to find a set of effects which can transform the sound of one voice to another specific one.
Another conclusion which may be drawn is that heuristic methods are a good choice to tackle the problem. This is because the search space for this problem is very large and heuristic methods are a convenient alternative to explore search spaces of this type due to their evaluation capability. Another important feature is that these methods can generate good candidate solutions in order to find an approximation close enough to the optimal solution.
Current work is being done on the system to test other heuristic methods. A preliminary version based on Ant Colony Optimization [9] has already been tested and the results are promising from an efficiency standpoint, but the correct execution requires the setting of many parameters. The use of other heuristic methods to solve this problem is also envisaged as future work. Nonetheless, genetic algorithms seem to work better than other heuristic methods so far.
Different fitness functions and mechanics for genetic operators continue to be explored and tested. It was found that the inclusion of these new features constantly improves the performance of the algorithm and quality of the found solutions. To continue to improve the system, a version in C is planned to be released and changes in the crossover operator, chromosome representation and fitness function are being actively researched.
Another feature which could be implemented as future work is the use of statistics in the system to automatically vary 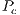 and
and 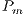 depending on the population state of an instance of the problem being solved.
depending on the population state of an instance of the problem being solved.
[1] M. Bozzo, M. Gutiérrez, and T. Bozzo, “Genetic algorithm based voice imitation system,” in Proceedings of the JCCC XXIX International Conference, 2010.
[2] Av voice changer. [Online]. Available: http://www.audio4fun.com/
[3] J. Holland, Adaptation in Natural and Artificial Systems. The MIT Press, 1992.
[4] M. Mitchell, An Introduction to Genetic Algorithms. The MIT Press, 1998.
[5] J. Cooley and J. Tukey, “An algorithm for machine computation of complex fourier series,” Math. Comp., pp. 297–301, 1965.
[6] G. Folland, Fourier analysis and its applications. Thomson Brooks/Cole, 1992.
[7] G. Marchuk, “Methods of numerical mathematics,” Journal of Applied Mathematics and Mechanics, 1975.
[8] MathWorks. Documentation center matlab r2010b. 2010.
[9] M. Dorigo, V. Maniezzo, and A. Colorni, “The ant system: Optimization by a colony of cooperating agents,” IEEE Transactions on Systems, Man, and Cybernetics part B, vol. 26, no. 1, pp. 1–13, 1996.