Introducción
La pandemia por SARS-CoV-2, un nuevo coronavirus surgido en 2019, con una historia natural desconocida, ha determinado una emergencia sanitaria y social mundial.
También ha generado, en un marco de gran incertidumbre, que la mayoría de los países del mundo adoptaran medidas no farmacológicas drásticas de control de la propagación de este virus, probadas como eficaces ya en 1918 con la epidemia de la gripe Española. Cada país optó por tomar acciones teniendo en cuenta su experiencia, analizando el impacto en las áreas de la salud, en lo económico y social, y aprendiendo de las experiencias comunicadas por otros países. Algunos optaron por estrategias de mitigación, intentando aplanar la curva de propagación, y otros por estrategias de supresión, para cortar la transmisión 1).
A nivel mundial se sigue con atención el comportamiento de la epidemia a través de la evolución de los datos aportados por los países en relación a la cantidad de test realizados según su población, el número de personas diagnosticadas como positivas y la cantidad de muertes por COVID-19.
Debido al porcentaje de infectados asintomáticos, la importante proporción de casos leves, así como a la heterogénea capacidad de testeo diagnóstico de los distintos países, han existido dificultades para estimar la incidencia real de la enfermedad en todo el mundo. Esto genera gran incertidumbre sobre la verdadera magnitud de la pandemia y su evolución 2).
Por este motivo, el desarrollo de modelos epidemiológicos para obtener curvas estimativas de la situación de la enfermedad en la población y así poder proyectar su evolución, adquiere especial importancia en un contexto de extrema incertidumbre, complejidad y dinamismo.
Esta ha sido la pandemia “de los modelos”: debido a la amplia disponibilidad de datos en tiempo real, múltiples instituciones académicas, gubernamentales, sociedades científicas, algunas con amplia experiencia en la materia, han desarrollado modelos tratando de proyectar la evolución de la pandemia. Se han publicado en Internet múltiples aplicaciones para el desarrollo de modelos “predictivos” de la pandemia. Sin embargo, en muchos casos estos modelos no reflejaron en forma adecuada la evolución de la pandemia.
¿Por qué la epidemia en Uruguay no ha evolucionado como inicialmente se esperaba? ¿Se equivocan los modelos matemáticos?
Debemos comenzar por comprender que los modelos matemáticos utilizados son representaciones simplificadas de la realidad, aún más compleja, para poder comprenderla. Su mérito radica en que sirven para tener aproximaciones a lo que puede estar pasando en un contexto de elevada incertidumbre, tratando de discriminar las “señales” del “ruido”.
La utilidad de los modelos radica en su capacidad para responder ciertas preguntas, como, por ejemplo, qué pasaría si se implementaran o no medidas de distanciamiento físico, si se mejorara o no la capacidad de respuesta del sistema sanitario, etc. Esto permite proyectar la evolución de la epidemia bajo distintos escenarios, lo que aporta un insumo más para la toma de decisiones.
George E. P. Box escribió que “en esencia, todos los modelos están equivocados, pero algunos son útiles” 3).
Tan importante como comprender qué son y para qué sirven los modelos es tener claro qué no son y qué no pueden decirnos. Los modelos proporcionan trayectorias, es decir, estimaciones de lo que podría suceder en un determinado contexto, bajo determinados parámetros y supuestos, con determinados datos, y considerando todas sus limitaciones potenciales. No son oráculos que permitan predecir o pronosticar qué va a pasar en el futuro.
El primer abordaje matemático de las epidemias se realiza en 1760 con Bernoulli y su modelo matemático para estudiar la viruela. Con los trabajos de L. Pasteur (1822 - 1895) y R. Koch (1843 -1910) se conocieron los mecanismos de trasmisión de una enfermedad, lo que permitió avanzar en el desarrollo matemático de modelos para explicar los mecanismos de propagación.
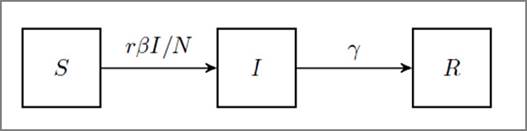
El primer modelo compartimental en el que cada individuo es clasificado en algún compartimiento vinculado con su estado de salud, fue desarrollado en 1906 por Hamer, quien plantea que “la tasa a la que se propaga una enfermedad es proporcional al número de individuos susceptibles de contraerla multiplicada por el número de individuos infecciosos” 4). En 1927 Kemack y McKendrick formulan el modelo SIR, que compartimenta a la población en susceptibles, infectados y recuperados, basado en un sistema de ecuaciones diferenciales de absoluta vigencia para esta pandemia (Figura 1) 4).
La formulación analítica del modelo representado en la figura 1, responde al siguiente sistema de ecuaciones diferenciales (Figura 2)
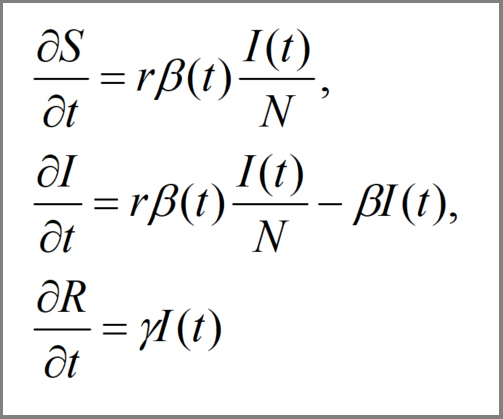
Figura 2: Modelo de ecuaciones diferenciales 𝑟: número de contactos por unidad de tiempo 𝛽: probabilidad de transmitir la enfermedad por contacto producido. 1 𝛾 :inverso del tiempo promedio de infección (para una persona)El número reproductivo básico 𝑅 0 = 𝑟𝛽 𝛾 , siendo:
Sobre la base de las formulaciones analíticas clásicas para el modelado de epidemias, podrían pensarse los modelos ya expuestos o variantes que incorporen otros niveles de complejidad, un mayor número de variables, relaciones entre ellas, parámetros y supuestos.
La construcción de estos modelos es siempre un proceso interactivo, que combina elementos conceptuales y operativos 5). Si bien es posible que modelos más complejos representen mejor la dinámica de la realidad, también pueden requerir un número excesivo de parámetros difíciles de estimar, especialmente en ausencia de datos locales y en relación a la historia natural de la enfermedad. En el otro extremo, modelos más simples, con menor exigencia en cuanto a cantidad de variables y parámetros pueden ser más adecuados en función de la cantidad y calidad de los datos disponibles y de la posibilidad de definir adecuadamente los parámetros necesarios, pero es posible que no logren simular adecuadamente la trayectoria observada.
Todo esto genera un nivel de incertidumbre importante que puede explicar en gran medida por qué a veces los modelos proyectan una evolución que no se ajusta a la realidad en el futuro. Los modelos matemáticos son, sin duda, herramientas extremadamente útiles, pero no infalibles.
Para complejizar más la situación, sobre la evolución natural de una pandemia se insertan particularidades locales, como la forma en la que se expande la epidemia (presencia de “superpropagadores” por ejemplo) y medidas de control implementadas en orden y tiempo establecido específicamente para cada realidad, todo lo que contribuye a modificar el curso de la epidemia, y deben ser consideradas en los modelos.
En el Uruguay se implementaron una serie de medidas globales para prevenir y controlar la transmisión de la infección por SARS-CoV-2. A nivel individual, se ha aconsejado el lavado frecuente de manos con agua y jabón, el uso de tapabocas, el control de la temperatura, la ventilación de los espacios cerrados y el distanciamiento físico 6,7). A nivel colectivo, se han recomendado medidas como la cuarentena de casos y contactos, el distanciamiento social, el cierre de espacios públicos, centros de enseñanza y fronteras, con alto nivel de acatamiento de acuerdo con algunas evaluaciones 8,9). Estas decisiones de alto impacto para el país se tomaron en ausencia de evidencia de alta calidad lo que ha generado controversias a nivel mundial y nacional con una polarización política alimentada por la incertidumbre 10). La realidad en relación a la evolución de la epidemia es tan compleja como dinámica.
Comprenderla y estructurarla en un modelo es un gran desafío, mayor aún si le sumamos la incertidumbre del impacto de las medidas de prevención y control y el momento en que los gobiernos las han implementado, así como el des escalamiento de las mismas. Hasta el momento la propagación de la enfermedad ha sido “lenta”, sin embargo, esta situación se pude revertir rápidamente a partir de cambios en medidas adoptadas o variaciones en el comportamiento de la población, que parecen mostrar un rol clave en el desarrollo de la epidemia.
Por tanto, la contribución de los modelos radica en la capacidad de generar distintos escenarios de evolución de la epidemia. Su capacidad de mostrar el efecto de determinadas medidas estará sujeto a que los modelos incorporen dentro de su estructura, parámetros que den cuenta del cambio en la intensidad de las medias (más rígidas o más flexibles). Esto es lo difícil de modelar. En la medida que se cuente con más información, estos elementos podrán ir incorporándose con mayor nivel de precisión de manera que los cambios que surjan en las trayectorias de los modelos reproduzcan adecuadamente la dinámica de la realidad.