Introducción
El incremento cuantitativo en la posibilidad de ingreso a la universidad ha puesto en evidencia la desigualdad en los niveles de formación, lo que lleva a reproducir las inequidades sociales (Gentili, 2009). Ello hace que las instituciones deban asumir la responsabilidad de evaluar su rol en la permanencia de los estudiantes en el sistema universitario, subrayando la importancia del acompañamiento en el proceso de transición de la enseñanza media a la universidad (Carbajal, 2014).
En la Facultad de Agronomía los cursos de matemáticas y estadística evidencian un alto nivel de reprobación y son percibidos por los estudiantes como los típicos cursos «filtro». Esta percepción es reforzada por las grandes disparidades en los niveles académicos de los estudiantes que ingresan. La brecha entre la formación del estudiante y los requerimientos de la institución, así como el incremento en la matrícula, no son problemas exclusivos del estudiante, sino un problema que la universidad debe atender (Carbajal, 2014). Este contexto nos plantea el desafío de comprender cómo los estudiantes procesan el abordaje de disciplinas como matemáticas y estadística en sus primeros años en la universidad, a los efectos de lograr procesos de acompañamiento eficaces.
Marco teórico
La investigación en lo que refiere a los procesos de enseñanza-aprendizaje en matemáticas se ha desarrollado bajo la égida del paradigma constructivista (Morales Urbina, 2009). En este paradigma el estudiante construye un significado basado en construcciones previas (Miras, 1999). Estas construcciones previas pasan a ser un elemento clave para la evolución en el proceso de aprendizaje, ya que los procesos constructivos posteriores van a estar condicionados por los significados construidos previamente y las estrategias que los generaron. Esta situación marca la necesidad de considerar los conocimientos iniciales del estudiante para facilitarle la nueva construcción sobre bases que permitan establecer una relación coherente entre lo que saben y lo que deben aprender (Barberá, 1999; Morales Urbina, 2009).
En este proceso de construcción, además de los conocimientos sobre la disciplina, las estrategias de aprendizaje son claves para asegurar el éxito (Schunk, 2008). Ghatala, Levin, Foorman y Pressley (1989) sugieren que al ingreso a la universidad el estudiante tiende a sobrevalorar su preparación y como consecuencia los resultados que obtiene con relación al tiempo y al esfuerzo empleados no suelen ser los esperados. En el estudio Evaluación diagnóstica en lectura y matemática a estudiantes que ingresan a carreras de la Udelar en el CURE, el Noreste y en las Facultades de Psicología y Ciencias Económicas (Fernández et al., 2017), se reporta que existen diferencias entre áreas de estudio, se observan mejores resultados entre estudiantes de las áreas de Ciencia y Tecnología, sin embargo también reportan la dificultad en las distintas operaciones matemáticas; álgebra es la de mayor dificultad, pero no es significativamente diferente de otras operaciones básicas. Este estudio muestra también la inexistencia de relaciones significativas entre los resultados en matemáticas variables como el sexo, la edad, el sector institucional donde cursaron enseñanza media o el capital cultural familiar.
Esto deriva en la necesidad de conocer las estrategias de aprendizaje del estudiante, enfocándose en el individuo, no solo como insumo para la docencia, sino para contribuir al desarrollo de esas estrategias a nivel individual y en el colectivo estudiantil. La investigación en este campo muestra que el uso de estrategias adecuadas es de relevancia para los procesos efectivos de aprendizaje (Ludwig, Finkbeiner y Knierim, 2013). Para Watt, Eccles y Durik (2006), los estudiantes con altas expectativas de éxito aprenden con mayor rapidez, mientras que los que tienen un interés particular en la disciplina van a estar más interesados y posiblemente sean más persistentes. Acee y Weinstein (2010) encontraron que prácticas que valorizan el uso de las matemáticas pueden incrementar el valor que los estudiantes dan a estos cursos y como consecuencia llevar a mejores performances.
Con este marco de referencia, este trabajo intenta proveer un diagnóstico del estudiante en su año de ingreso a la Facultad de Agronomía a partir del diagnóstico de sus conocimientos básicos, sus estrategias de aprendizaje y su rendimiento en el curso de matemáticas de primer año.
Materiales y métodos
A los efectos de ajustar el diagnóstico a la generación 2017, se aplicó una prueba al inicio del curso sobre conocimientos básicos de matemáticas, desde operaciones básicas hasta un mínimo conocimiento de cálculo y una adaptación del inventario sobre aprendizaje de VanderStoep y Pintrich (2008).
La investigación está planteada desde una perspectiva cuantitativa, se busca una interpretación de los datos obtenidos como forma de comprender al estudiante al ingreso y generar una plataforma para el desarrollo de estrategias de enseñanza-aprendizaje. El inventario de aprendizaje fue diseñado para identificar fortalezas y debilidades en las estrategias y la motivación de los estudiantes con relación al aprendizaje, y propone seis escalas: establecimiento de objetivos, motivación, manejo de recursos (organización del tiempo, materiales, clases de apoyo), metaconocimiento, pensamiento crítico y resolución de problemas. El inventario fue traducido al español y adaptado a las formas de lenguaje habituales en Uruguay. Este instrumento apunta a la valoración del aprendizaje autorregulado, e incluye no solo aspectos cognitivos, sino también motivacionales y afectivos (Pintrich, 2004).
La prueba de matemáticas fue preparada por los docentes a cargo del curso de Métodos Cuantitativos I; se tomaron en cuenta y se revisaron los programas de Matemática de los últimos dos años de bachillerato de Educación Secundaria (Consejo de Educación Secundaria, 2006) y Educación Media Tecnológica (2004). Se utilizó el Scholastic Assesment Test (SAT) (Daniel, 2010), prueba utilizada para evaluar la preparación de los estudiantes de bachillerato antes de la entrada a la universidad en los Estados Unidos, que cuenta con una sólida trayectoria. Se elaboraron estándares agrupados en cuatro categorías: números, operaciones básicas, álgebra y cálculo, y a todas las categorías se les otorgó igual puntaje.
La población estudiada fueron los estudiantes inscritos en el curso Métodos Cuantitativos I en el año 2017. La prueba diagnóstica fue aplicada a 577 estudiantes y el inventario de aprendizaje fue completado por 320. Los resultados finales se analizaron sobre una base de 580 estudiantes que completan al menos una de las pruebas parciales del curso. Los resultados de la primera fecha de examen se analizaron sobre un total de 103 estudiantes que cursaron en 2017. Cabe señalar que el curso 2017 tuvo un 62 % de nuevos ingresos y un 38 % de recursantes. Se utilizaron técnicas descriptivas uni- y bivariadas, y análisis de componentes principales a los efectos de comprender la estructura de los datos, de manera de detectar patrones de comportamiento. Se utilizó el software InfoStat (Di Rienzo, Casanoves, Balzarini, González, Tablada y Robledo, 2011).
Resultados y discusión
Los resultados de la prueba diagnóstica sobre conocimiento básico de matemáticas muestran que solo 2 % de los estudiantes superan el 50 % de la prueba y 91 % no superan el 30 % (tabla 1).
Tabla 1: Resultados de la prueba diagnóstica de conocimientos en matemáticas. Porcentaje de estudiantes según puntaje obtenido
| Puntaje | % de estudiantes |
| 0-10 | 91 |
| 10-15 | 7 |
| 15-20 | 1 |
| 20-30 | 1 |
Nota: Sobre un total de 577 estudiantes.
Las características de la prueba, en la que la exigencia tanto de operaciones como de cálculo era básica, hacen que los resultados nos lleven a reflexionar sobre sus causas. El estudiante al ingreso tiende a sobrevalorar su preparación y a mantener una motivación extrínseca; si no existe un mecanismo de transacción, obtención de algún beneficio, puntos, créditos, no suele estar motivado a realizar evaluaciones, concurrir a clases de apoyo, hacer consultas online o recurrir a algún otro mecanismo de enseñanza-aprendizaje fuera de lo obligatorio. En este caso la prueba diagnóstica no aportaba puntaje para el curso.
Los resultados finales del curso fueron otro indicador cuantitativo: el 61 % de los estudiantes reprueban, con lo que se mantiene el porcentaje histórico (tabla 2).
Tabla 2: Porcentaje de estudiantes según puntaje obtenido en el curso
| Puntaje | % de estudiantes | % acumulado |
| 0-20 | 14 | 14 |
| 20-40 | 37 | 51 |
| 40-50 | 10 | 61 |
| 50-60 | 21 | 81 |
| 60-70 | 11 | 93 |
| 70-80 | 3 | 96 |
| 80-100 | 4 | 100 |
Nota: Sobre un total de 580 estudiantes que hicieron por lo menos una prueba parcial.
De estos resultados se desprende que el 51 % que reprobaron no lograron superar el 40 % de los puntos del curso, solo 10 % quedaron en una zona límite sin alcanzar el 50 % más 1 de los puntos, porcentaje de aprobación, y el 39 % aprobaron. Los resultados evidencian dos poblaciones, una que aprueba el curso con puntajes de entre 50 y 70, y otra que no lo aprueba con puntajes de entre 0 y 40, sobre un total de 100 puntos. Son pocos los estudiantes que quedan en una situación intermedia. Solo el 4 % de los estudiantes alcanzaron el 80 % de los puntos y lograron la exoneración.
Los resultados del primer examen del período para los estudiantes de la generación 2017 reflejan la misma tendencia. Hay un 36 % de aprobación y un 74 % de reprobación (tabla 3).
Tabla 3: Porcentaje de estudiantes según puntaje obtenido en el examen
| Puntaje | % de estudiantes |
| 0-20 | 12 |
| 20-50 | 52 |
| 50-60 | 8 |
| 60 y más | 28 |
Se analizó la relación entre los puntajes obtenidos en la prueba diagnóstica y el resultado final del curso, de lo que se obtuvo una correlación que, si bien es significativa, es débil (p < 0,0001; r = 0,37). Este resultado puede explicarse también por la sobrevaloración de los conocimientos previos y/o por la falta de motivación extrínseca, dado que el resultado de la prueba diagnóstica no aportaba puntos al total del curso. Estos resultados se alinean con los resultados del estudio de Fernández et al. (2017).
El inventario de aprendizaje, que fue el segundo de los indicadores cuantitativos aplicados, tuvo el objetivo de identificar fortalezas y debilidades en el aprendizaje. El inventario propone seis ítems: establecimiento de objetivos, motivación, manejo de recursos (organización del tiempo, materiales, clases de apoyo), metaconocimiento, pensamiento crítico y resolución de problemas (véase la tabla 4).
Tabla 4: Resultados obtenidos a partir del inventario de aprendizaje sobre un total de 320 estudiantes que completan el formulario
| Variable | Medias teóricas | Media | Coeficiente de variación | Mediana | Primer cuartil | Tercer cuartil |
| Metas | 2,76 | 2,49 | 17,89 | 2,60 | 2,20 | 2,80 |
| Motivación | 2.86 | 2,57 | 18,42 | 2,50 | 2,17 | 3,00 |
| Recursos | 2,46 | 2,55 | 12,53 | 2,56 | 2,39 | 2,78 |
| Metaconocimiento | 2,72 | 2,27 | 30,40 | 2,20 | 1,80 | 2,60 |
| Pensamiento crítico | 2,58 | 2,33 | 27,83 | 2,40 | 2,00 | 2,80 |
| Resolución de problemas | 2,93 | 2,26 | 24,30 | 2,25 | 2,00 | 2,50 |
De los resultados se desprende que en todos los ítems, excepto el manejo de recursos, solo el tercio superior alcanza los valores teóricos esperados de un estudiante a nivel universitario. En la tabla 5 se muestran los porcentajes de estudiantes que alcanzaron las medias teóricas de las variables estudiadas.
Tabla 5: Porcentaje de estudiantes que alcanzan o superan la media teórica según variable
| Variable | % de estudiantes |
| Metas | 32 |
| Motivación | 18 |
| Recursos | 56 |
| Metaconocimiento | 3 |
| Pensamiento crítico | 28 |
| Resolución de problemas | 11 |
El ítem de menor porcentaje es el de metaconocimiento, definido por VanderStoep y Pintrich (2008) como la conciencia y el control de los mecanismos de aprendizaje que cada individuo posee. El conocer la forma en que se aprende ayuda a conocer los límites y, de esa forma, ajustar las estrategias de aprendizaje para lograr un mejor desempeño. El ítem de resolución de problemas es el que sigue en términos de menores porcentajes; este indicador es definido como la acción de evolucionar desde no poder completar un trabajo a ser capaz de hacerlo (VanderStoep y Pintrich, 2008).
La motivación definida como la fuerza que dirige el comportamiento está directamente vinculada con la autorregulación (Pintrich, 2004), el estudiante motivado realiza actividades que cree que serán beneficiosas para alcanzar sus metas. Es así que la autorregulación promueve el aprendizaje, y como consecuencia de un aprendizaje eficiente y efectivo, se mantienen la motivación y la autorregulación para lograr nuevos objetivos (Schunk y Ertmer, 2000). Los resultados muestran que solo el 18 % de los estudiantes aparecen como motivados, lo que evidencia que es necesaria una estrategia para guiar al estudiante en la búsqueda de mecanismos para lograr una forma eficiente y efectiva de aprender. El establecimiento de metas y el uso de recursos son los ítems que presentan mejores resultados. El establecimiento de metas es una forma de ordenar pensamientos y acciones; sin embargo, si estos no están claramente definidos, no cumplirán con esa función (VanderStoep y Pintrich, 2008). Con relación al manejo de recursos tanto humanos como materiales a fin de maximizar el aprendizaje, existe una brecha considerable para el estudiante en su transición de secundaria a la universidad. El estudiante de secundaria tiene actividades pautadas, reguladas y controladas, que lo obligan a autorregularse; situación que cambia drásticamente con el ingreso a la universidad.
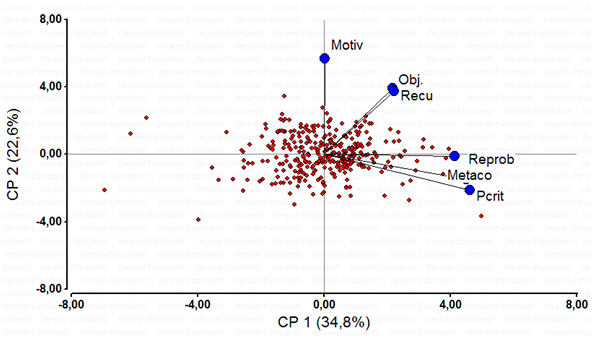
El análisis de componentes principales para el inventario de aprendizaje se realizó a los efectos de identificar las variables que explican la mayor parte de la variabilidad del conjunto de variables estudiadas. Se identificaron dos componentes que explicaron el 57,4 % de la varianza. El componente 1 el 34,8 %, y el componente 2, el 22,6 %. Las nuevas variables son combinaciones lineales de las anteriores que se van construyendo según la variabilidad total que recogen, no correlacionadas entre sí. La tabla 6 muestra las correlaciones de cada uno de los componentes con las variables originales.
Tabla 6: Correlaciones con las variables originales
| Variables | Componente 1 | Componente 2 |
| Metaconocimiento | 0,79 | -0,21 |
| Objetivos | 0,38 | 0,55 |
| Motivación | 0,00 | 0,80 |
| Recursos | 0,39 | 0,53 |
| Resolución de problemas | 0,79 | -0,02 |
| Pensamiento crítico | 0,81 | -0,30 |
El componente 1 reúne las variables metaconocimiento, resolución de problemas y pensamiento crítico, mientras que el componente 2 reúne las variables objetivos, motivación y manejo de recursos. En el gráfico 1 puede visualizarse la dispersión de las observaciones. El gráfico muestra simultáneamente las variables (vectores) y las observaciones (puntos). Lo que se interpreta son las direcciones y ángulos entre vectores, que representan las correlaciones entre variables. Ángulos de 90 grados entre dos variables indican que estas no se encuentran correlacionadas, ángulos cercanos a 0 indican que están altamente correlacionadas (Stevens, 2009). Cabe señalar que el método de componentes principales es descriptivo y no inferencial.
El componente 1 puede interpretarse como la caracterización de un estudiante con un mayor potencial de autorregulación, mientras que el componente 2 puede verse como la caracterización de un estudiante motivado fundamentalmente por sus objetivos y los recursos que posee. Como puede observarse, hay una gran dispersión. Identificados los individuos que generan la inercia del componente 1 (los más alejados), predominan los que aprobaron el curso, pero también los hay que reprueban. Con relación a los valores menores que 0 para este componente, los individuos que más se alejan reprobaron el curso. En el componente 2, las observaciones que generan la inercia se corresponden en el eje positivo con estudiantes que reprueban en general, y en los valores negativos predominan los que aprueban.
Los resultados del análisis de componentes principales articulan con el estudio descriptivo del inventario de aprendizaje. Las variables que tienen más peso en la explicación de los resultados son las más vinculadas a la autorregulación, el metaconocimiento, la capacidad de resolución de problemas y el pensamiento crítico. El porcentaje de estudiantes que presentaron valores cercanos a los teóricos para dichas variables fue bajo.
De los resultados se desprende que la prueba diagnóstica no fue un buen indicador del desempeño en el curso, mientras que el inventario de aprendizaje surge como un indicador más ajustado para predecir un comportamiento autorregulado y, como consecuencia, mejores resultados académicos.
Este diagnóstico plantea un escenario favorable para desarrollar las variables que estimulan la autorregulación, aplicándolas a la creación de estrategias de enseñanza-aprendizaje. Generar mayor responsabilidad y autonomía en un contexto que promueva la autorregulación. Pintrich (2004) señala que los modelos de enseñanza que se centran en el estudiante propenden a un mayor control y regulación del trabajo y del contexto.