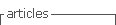Implicaciones prácticas
La propuesta elaborada sobre la base de los hallazgos detectados en el estudio tiene una connotación significativa en la práctica educativa. Los profesores dirigen la enseñanza de la disciplina Matemática evidenciando fisuras entre el contenido teórico, su relación con el contexto, y la comprensión y el nivel de aplicación de lo aprendido por los estudiantes en la vida cotidiana, lo que ocasiona bajos resultados en la resolución de problemas. Se reconoce que el proceso de aplicabilidad del contenido de las matemáticas en la vida real debe ser un principio orientado a la educación de esta disciplina. El propósito es estimular el razonamiento de los estudiantes a través de hechos prácticos, a fin de asimilar el contenido teórico y aprender a aplicarlo ante situaciones y problemas cotidianos. El ciclo didáctico debe comenzar desde la experiencia, acceder al saber teórico y luego volver a la práctica con el propósito de aplicar lo aprendido; este debe ser el objetivo central de esta disciplina curricular. Esta propuesta transformará la enseñanza matemática, convirtiendo a los profesores en guías apasionados. La metodología empodera a estudiantes para comprender procesos, nutriendo habilidades críticas y generando alegría y confianza en desafíos matemáticos. Salones vibrantes promueven curiosidad y descubrimiento, abrazando errores como trampolines hacia un entendimiento profundo.
Introducción
El desarrollo científico y tecnológico digital ha generado un volumen exponencial de información en todas las áreas del conocimiento. Para abordar este desafío, los sistemas educativos deben implementar métodos que potencien el desarrollo del pensamiento lógico y crítico en los estudiantes. Esto les permitirá asimilar, procesar y aplicar la información aprendida en la solución de problemas académicos y cotidianos (Morin, 2011).
En el diseño curricular de Secundaria del Ministerio de Educación del Perú (2016) se destaca la necesidad de estimular el pensamiento lógico, adquirir conocimientos y desarrollar habilidades intelectuales y prácticas en los estudiantes de la disciplina de Matemáticas. Esto implica la capacidad de asimilar, procesar, comprenderla y aplicar la información en la resolución consciente de problemas, tanto en entornos académicos como en la vida social.
Por su parte, el Programa Internacional de Evaluación de Estudiantes (PISA, 2018) en Perú reveló un bajo nivel cognitivo y habilidades insuficientes en la resolución de problemas matemáticos entre los estudiantes de Secundaria. Este resultado impulsó la implementación de programas de mejora que se enfocaron en la preparación teórica y didáctica de los docentes para optimizar su desempeño en la enseñanza-aprendizaje.
En respuesta a los cambios continuos en el diseño curricular de Matemáticas, los docentes deben transformar su enfoque en el aula para fomentar el razonamiento y la resolución de problemas (Ader, 2019). Frente a esta realidad, el Ministerio de Educación de Perú y otros organismos han desarrollado planes de capacitación para empoderar a los docentes en la aplicación de metodologías activas y medios audiovisuales, con el propósito de potenciar el pensamiento crítico, la reflexión y la comprensión sobre cómo abordar y resolver problemas matemáticos, así como controlar el proceso de aprendizaje.
Acerca de la resolución de problemas, Pólya (1987) propone un método que orienta al profesor en su tratamiento e incentiva a los estudiantes. De igual forma, Vargas (2021) propone una metodología en la que demuestra cómo la resolución de problema influye en el pensamiento lógico; mientras que Díaz y Careaga (2021) sugieren tratar este contenido partiendo de la experiencia del contexto de los alumnos, de los problemas que observan en el medio social. Estos últimos autores enfatizan que cuando el aprendiz relaciona las experiencias con la nueva información es capaz de procesarla y comprenderla hasta integrarla, concientizarla y fijar lo aprendido de manera significativa.
A pesar del avance de los aportes de los teóricos y las investigaciones, persisten deficiencias en el tratamiento y el aprendizaje de la competencia de resolución de problemas. En ese sentido, Martínez (2018) y Mendoza (2019) advierten que en la práctica se perciben limitaciones en los educandos en el razonamiento de la información para procesarla, al identificar problemas del contexto, dificultades en la aprehensión de las acciones en la ejecución y en general a la carencia de conocimientos y destrezas sobre el qué hacer, el cómo hacer, cuál es el resultado y el autocontrol del producto de la actividad.
Estas deficiencias han generado debates profesionales y la búsqueda de información en investigaciones, enfoques teóricos, metodologías y actividades que ayuden a transformar la problemática presente en el proceso de enseñanza-aprendizaje de Matemáticas. En este contexto, se reconoce el valor del uso de herramientas digitales que, por su naturaleza audiovisual, estimulan la comunicación, observación, concentración y motivación. Además, facilitan que los estudiantes, siendo nativos digitales, se sientan atraídos, experimenten la necesidad de interactuar, indagar y exponer sus ideas ante sus compañeros y utilicen estos recursos como vía para descubrir lo nuevo.
Investigaciones realizadas por Iriarte y Sierra (2011) y Pérez (2014) coinciden en que la enseñanza orientada a la resolución de problemas desde perspectivas y estrategias metacognitivas garantiza la activación e influencia en procesos cognitivos, reflexivos, afectivos, volitivos y motivacionales. Estos inciden en actitudes positivas y en el desarrollo de la independencia cognitiva, la autorreflexión, autorregulación y autocontrol por parte de los estudiantes (De Corte, 2015).
Asimismo, las investigaciones efectuadas por Vargas (2021) coinciden en que la enseñanza orientada a la resolución de problemas requiere de nuevos enfoques y visiones paradigmáticos para emplear los métodos activos, problémicos y que enfaticen en las formas de enseñar y de aprender. Es preciso superar la tendencia de privilegiar las abstracciones en detrimento de la aplicabilidad de este contenido en los contextos reales y en la vida práctica. En ese sentido, Díaz y Careaga (2021) aseveran en su estudio que la enseñanza de la resolución de problemas exige de nuevas taxonomías basadas en los sustentos teóricos y didácticos, con proyección de explorar una teoría matemática que permita despejar su cientificidad en el arraigo contextual de sus problemas, para no quedar reducida a la sola formulación de enunciados abstractos.
El desarrollo de las habilidades de resolución de problemas es un objetivo central en la disciplina de Matemáticas debido a su incidencia en el pensamiento, la comprensión de procesos, actitudes, la asunción de posiciones críticas y la interacción con compañeros. Sin embargo, se constatan dificultades en el grupo de cuarto grado del área de Matemáticas, evidenciadas en el bajo nivel de conocimientos, la falta de aplicación de algoritmos matemáticos, habilidades reflexivas, indagación, interpretación y contextualización del contenido. Asimismo, se observa la necesidad de concientizar los procesos seguidos y cómo aplicar lo aprendido en la resolución de problemas (Arteaga et al., 2020).
El objetivo de esta investigación se orienta a analizar el nivel de desarrollo de la competencia de resolución de problemas y proponer un modelo de estrategia metacognitiva que contribuya a la transformación de la problemática en los estudiantes de cuarto grado del área disciplinar de Matemáticas de Secundaria de una institución educativa peruana.
Reflexiones sobre la resolución de problemas matemáticos
La resolución de problemas matemáticos se define como la superación de dificultades en situaciones novedosas mediante el pensamiento lógico-matemático. El alumno utiliza este enfoque para obtener información desconocida a partir de información conocida, aplicando reglas lógicas de procesamiento matemático para llegar a la solución (Cuello et al., 2021).
La resolución de problemas no solo facilita el aprendizaje de Matemáticas, sino también el desarrollo del pensamiento lógico en los estudiantes. Sin embargo, la práctica común de los docentes de centrarse en ejercicios repetitivos de algoritmos o la aplicación de fórmulas al finalizar los contenidos resulta poco efectiva para cultivar habilidades y destrezas relacionadas con el razonamiento lógico-matemático (Contreras et al., 2021).
La resolución de problemas matemáticos contribuye al pensamiento lógico, crítico, la reflexión y a desarrollar habilidades para aplicar lo aprendido en la práctica. Un precursor de ese objetivo es Pólya (1987), quien plantea que resolver un problema implica encontrar un camino alrededor de un conflicto y la solución a un problema desconocido. Pólya agrega que cuando el docente enseña a los estudiantes los procedimientos para resolver un problema, los coloca frente a una actitud reflexiva sobre cómo abordarlo. Esto los enfrenta a una contradicción generada por la actividad desconocida sobre la que no tienen los procedimientos ni los recursos para resolverla. De ahí que surja la contradicción cognitiva, procedimental y actitudinal que es necesario desencadenar.
En ese sentido, Guzmán (1995) sostiene que un problema matemático es un auténtico reto que coloca al sujeto ante una situación que debe resolver para estimular el pensamiento, los conocimientos previos y las experiencias que posee su contexto. Esa perspectiva sugiere que, para lograr la solución, el estudiante tendrá que leer, asimilar la información proporcionada, releer el problema para comprender los datos, relacionarlos con sus experiencias e integrarlos ejercitando las operaciones lógico-matemáticas que lo guían la resolución (Goñi, 2008; Kılıç, 2017).
En relación con esto, Pólya (1989) propone los pasos metodológicos que deben seguirse: entender el problema, identificar la etapa donde se establece la incógnita, los datos y las condiciones; concebir un plan, relacionar hechos semejantes con el problema objeto de estudio; ejecutar el plan, donde el sujeto realiza cada paso evidenciando dominio a lo largo de su ejecución hasta el final; y, por último, examinar la solución, que constituye un momento de visión retrospectiva del proceso y el resultado alcanzado. En esta fase, el sujeto se detiene a observar y verificar qué hizo, cómo lo hizo y cuál es el resultado obtenido de manera general.
Esta perspectiva exige de la aplicación de métodos que ejerciten el pensamiento lógico, la reflexión, los saberes previos, la significatividad del objeto. También implica problematizar en la búsqueda de la solución hasta llegar a conclusiones, enfatizando en los aspectos conceptuales, procedimentales y actitudinales, y su aplicación a través de actividades variadas donde se ejerciten y consoliden las habilidades integrales (Tobón, 2013).
Desde estas perspectivas, se reconoce que el objetivo de la resolución de problemas es un contenido esencial cuando se aborda desde una enseñanza interactiva que estimula el pensamiento e incentiva el interés en los estudiantes (Chirinda & Barmby, 2017). Esto requiere de metodologías problémicas, investigativas y colaborativas, donde el educando es un ente participativo que observa, asimila, interpreta, llega a conclusiones y aplica lo aprendido de manera crítica, metacognitiva. Esto lo prepara para enfrentarse a la solución de problemáticas académicas y de la realidad (Özsoy et al., 2015).
La metacognición y su incidencia en la resolución de problemas
En las últimas décadas, se aprecia un consenso entre pedagogos e investigadores respecto a que la metacognición es una vía esencial para lograr un aprendizaje consciente. Flavell (1976) sostiene que la metacognición es un proceso de cognición sobre la cognición, pensar sobre el pensamiento y conocer sobre el conocimiento. Implica ser consciente de la propia conciencia como parte de un proceso intelectual que potencia el autoconocimiento y el desarrollo de habilidades de orden superior del pensamiento e integrales.
En estas perspectivas, Flavell propone dos aspectos intrínsecos a la metacognición: el autoconocimiento de los procesos cognitivos y la regulación de estos. El primero, de naturaleza declarativa, se concreta en tres dimensiones: la persona, las tareas y las estrategias. El segundo se refiere al aspecto procedimental o saber hacer, permitiendo al estudiante aplicar acciones y operaciones de manera coherente para cumplir el objetivo. En este último, destacan tres procesos correspondientes a las tres fases de la solución de un problema: la planificación, el control y la evaluación.
En esta misma línea, la metacognición involucra las diversas estrategias que un estudiante elige al resolver un problema, según la efectividad percibida de un método o la necesidad de superar obstáculos durante el proceso de resolución. Se trata de la reflexión y adaptación consciente del estudiante en función de su experiencia en la solución de problemas (Fuentes & Miranda, 2023).
Por otro lado, la metacognición aplicada a la enseñanza exige del estudiante que conozca su pensamiento, sus fortalezas, dificultades y los procedimientos para actuar, según plantean Castellanos et al. (2007). Es una alternativa coherente para contribuir a la formación consciente de los procesos cognitivos del pensar, qué aprenden, cuánto aprenden, qué necesitan aprender, qué significado tiene lo que aprenden y cómo aplicar lo aprendido en la práctica de forma autorregulada (Gómez & Godoy, 2010; Perrone, 2011; Jasso, 2014).
En esa dirección, Mayor (2009) advierte que la resolución de problemas es una actividad intelectual que moviliza los procesos lógicos del pensamiento, ejercita los saberes previos, la creatividad, y potencia la reflexión del educando sobre su propio aprendizaje y la toma de decisiones. De ahí que la metacognición sea una vía para un aprendizaje consciente de la resolución de problemas, fomentando la independencia cognitiva, las habilidades de aprender a aprender, la autorregulación y la autonomía estudiantil (Pérez, 2014; Arteaga et al., 2020).
Como se aprecia, concebir la resolución de problemas desde la enseñanza metacognitiva requiere del empleo de métodos activos que privilegian el protagonismo estudiantil en el pensamiento para construir el conocimiento y ejercitar las habilidades correspondientes a las fases metacognitivas que plantea Brown (1987), la reflexión (conciencia para reconocer la disposición cognitiva), la administración (regulación y control del aprendizaje antes, durante y después) y la autoevaluación de los procesos cognitivos desplegados en la tarea (Hernández, 2014; Fernández & Aguado, 2017).
Las investigaciones de Iriarte y Sierra (2011) y Pérez (2014) aseveran que esta enseñanza provoca un cambio cualitativo superior en el aprendizaje de los contenidos matemáticos (Rajadurai & Ganapathy, 2023). Tal resultado se obtiene por el nivel de motivación e interés al disponer el educando de las herramientas a fin de proceder, por la curiosidad que experimenta y que lo induce a tomar decisiones en la búsqueda de soluciones a través del intercambio de ideas con sus iguales, la socialización y la ayuda mutua donde se autoevalúan, explican sus avances, las dificultades y se ponen metas superiores como consecuencia de la autorregulación (De Corte, 2015; Donoso et al., 2020).
Las estrategias metacognitivas, una vía para estimular el aprendizaje
En relación con las estrategias metacognitivas, Jasso (2014) y Mato et al. (2016) sostienen que están integradas por un conjunto de acciones conscientes y autorreguladas que pone en práctica el sujeto al planificar la actividad, monitorear las acciones y evaluar la calidad de las operaciones ejecutadas. Son habilidades que estimulan los procesos mentales: dominio del contenido (qué), saber utilizarlo (cómo), saber reajustar las acciones cuando así lo requiera el producto.
Una consideración similar aporta Álvarez de Zayas (2016), al expresar que las estrategias cognitivas y metacognitivas son procesos que revelan cómo organizar las acciones en un determinado ejercicio por parte del educando. Se concretan en operaciones potenciadoras de los procesos mentales de comprensión y concientización que conducen a la solución del problema o cualquier actividad, dependiendo del contenido, las exigencias de la tarea y de la planificación, el control, la evaluación por el propio educando y el grupo (Castellanos et al., 2007).
En línea con ello, Monereo y Pozo (2008) refieren que las estrategias metacognitivas están conformadas por un proceso secuencial que necesita de varias habilidades: primero, la modelación metacognitiva, donde el estudiante imita las acciones cognitivas expresándose verbalmente; segundo, análisis y discusión metacognitiva, que consiste en reflexionar sobre cómo hacer la tarea, qué ha pensado e imaginado para resolverla; y tercero, la autointerrogación, a través de una serie de preguntas durante y después de la tarea, ejercitando el autocontrol y la autoevaluación del proceso y el logro alcanzado (Castro et al., 2020).
Su propuesta se sostiene en los métodos heurísticos y en los pasos metacognitivos: planificación, predicción, regulación, control, verificación y aplicación de los tres momentos: antes (previo a realizar la tarea, predecir los resultados y planificar los objetivos); durante (ejecución, regula, controla, ensaya y rectifica sus acciones) y después (momento de la evaluación, emite juicio, realiza preguntas reflexivas, se responde y autocorrige su resultado).
En ese sentido, Hernández (2014) y Mato et al. (2016) aseveran que el aprendizaje concebido desde esta óptica influye en el pensamiento y en la actitud consciente del sujeto al expresar lo que piensa, lo que sabe y lo que no sabe al planificar, monitorear y evaluar el proceso y el resultado de la actividad. En este quehacer, ejercita la autoevaluación, toma conciencia de sus fortalezas, de sus fallas, se explica la causa y ponen en acción las habilidades de aprender a aprender de forma autónoma.
De este modo, la enseñanza privilegia los procedimientos metacognitivos enfatizando que el estudiante asimile la información, la procese, la analice, asuma posiciones de forma crítica al construir el conocimiento y ejercite las habilidades que lo hacen consciente del cómo y cuándo aplicar lo aprendido, practicando el autocontrol, autorregulación, autoevaluación y la autoorganización de su proceder al solucionar problemas (Flavell, 1976; Perrone, 2011).
Como se ha analizado, las estrategias metacognitivas devienen en destrezas que favorecen la fijación, apropiación y descubrimiento del contenido y del proceso seguido por el estudiante para arribar al producto final. Su uso sistemático influye en el razonamiento, el interés y las emociones positivas por la satisfacción que genera en él saberse consciente de su actuación al ejercitar las habilidades de coevaluación, autoevaluación, autocontrol, la autorregulación y la independencia cognoscitiva en general (Castellanos et al., 2007).
Se ha enfatizado que estas estrategias propician que el aprendiz autodirija sus propios procesos mentales y las acciones que debe ejecutar de manera personal y en colaboración con sus iguales donde todos opinan, debaten, aportan ideas y realizan las actividades en un ambiente de confraternidad, respeto y comunicación asertiva que les impulsa a transitar de un estado real de desarrollo a uno superior integralmente (Vygotsky, 1978).
Metodología
La metodología de la investigación se fundamenta en el paradigma sociocrítico y responde a una investigación educativa de tipo aplicado, con un nivel transformativo. El diseño adoptado fue el anidado concurrente de modelo dominante, ya que los datos del trabajo de campo, tanto cuantitativos como cualitativos, se recolectaron de manera simultánea, con preeminencia de los datos cualitativos (Hernández et al., 2014). Desde una perspectiva dialéctica, se integran los métodos cuantitativos y cualitativos en el estudio del fenómeno educativo. En este enfoque, el investigador parte de su experiencia en el aula y, mediante el método científico, sistematiza las categorías apriorísticas, las contrasta con la realidad del diagnóstico de campo, identifica las causas que inciden en el problema y propone soluciones (Mosteiro & Porto, 2017; Hernández & Mendoza, 2018).
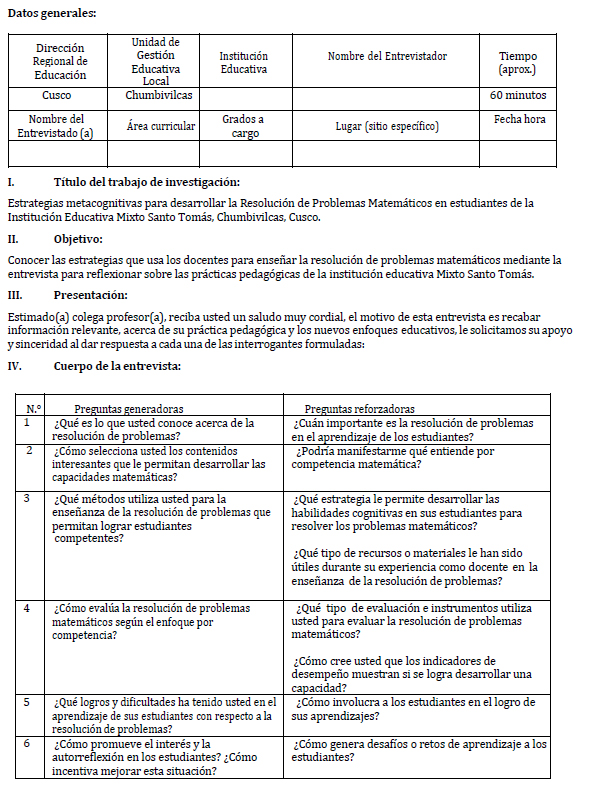
El estudio empleó diversas técnicas de recopilación de información, tales como la entrevista en profundidad, la observación y la encuesta. Los instrumentos utilizados fueron los siguientes: una guía de entrevista semiestructurada compuesta por seis preguntas generadoras y ocho preguntas reforzadas, una guía de observación con ítems que abordan cuatro subcategorías (programación curricular, procesos pedagógicos, recursos y materiales, evaluación), un cuestionario compuesto por nueve preguntas abiertas y una prueba pedagógica que consta de 14 preguntas con tres alternativas de respuesta, siendo una de ellas la correcta y las otras incorrectas. Todos estos instrumentos fueron validados mediante el criterio de expertos (Galindo, 2020) y se encuentran en el Apéndice A.
La muestra estuvo conformada por 86 estudiantes de secundaria, seleccionados por muestreo no probabilístico, a criterio del investigador, a quienes se les aplicó el cuestionario y la prueba pedagógica, y seis docentes a quienes se les aplicó la entrevista a profundidad y la observación con el propósito de constatar el dominio teórico y didáctico al guiar la enseñanza-aprendizaje.
La validez de los instrumentos se realizó por criterio de cinco jueces expertos en el área de matemática y metodólogos. La interpretación de los datos se basó en lo que plantea Escurra (1988), quien sostiene que los reactivos o ítems cuyos valores sean iguales o mayores a 0,80 son considerados válidos para la prueba. En la Tabla 1 se observa la validez de V de Aiken realizada por tres criterios: relevancia, pertinencia y construcción gramatical.
Según la V de Aiken de los instrumentos se puede observar que todos tienen un alto grado de validez de contenido. Por otra parte, se calculó la confiabilidad de los instrumentos cuantitativos, el cuestionario y la prueba pedagógica. Para ello se aplicó el α de Cronbach y se obtuvo un puntaje de 0.955 para el cuestionario y 0.823 para la prueba pedagógica, lo cual indica una alta confiabilidad. T2
Propuesta de una estrategia metacognitiva
Se propone una estrategia metacognitiva basada en una concepción dialéctica integradora del enfoque sociocrítico, con el fin de estimular el aprendizaje desde posiciones reflexivas, potenciando las capacidades de autorreflexión con la intención de fomentar el autoconocimiento, el proceso seguido en la actividad y su resultado (Castellanos et al., 2007; Ortiz, 2015; Addine et al., 2015).
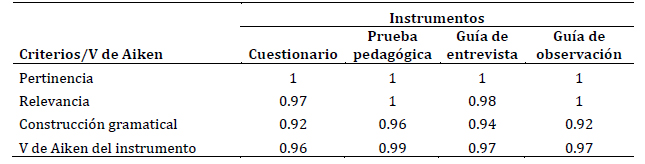
El modelo elaborado (Figura 1) privilegia partir de una secuencia problematizadora del contenido que incida en el debate, la toma de decisiones y la resolución de problemas matemáticos. Unido a los procedimientos metacognitivos como eje transversal de la enseñanza-aprendizaje, se estimula un aprendizaje consciente, reflexivo, analítico y dialógico que contribuye a que el estudiante se apropie del conocimiento y de las acciones del proceso, fomentando el autoaprendizaje y la autorregulación de su actuación de manera autónoma.
Esta concepción didáctica promueve el desarrollo integral del estudiante a partir de la realización de tareas diferenciadas que consideran los niveles de desarrollo actuales del sujeto. Además, orienta y guía para arribar al potencial, lo cual conduce el tránsito continuo hacia niveles superiores de desempeño, incidiendo en la formación de una personalidad integral y autodeterminada, capaz de transformarse y de contribuir a la transformación de su realidad en un contexto histórico concreto (Castellanos et al., 2007).
Esa forma de concebir el estudio fortalece los procesos lógicos del pensamiento, amplía las capacidades y conocimientos, y en general, ejercita las habilidades cognitivas y metacognitivas que promueven el autoconocimiento, el aprender a aprender y el autocontrol. En tal sentido, la neuroeducación acentúa que la emoción y la curiosidad activan la concentración, el interés, la afectividad y la alegría en los aprendices, fomentando un conocimiento sólido (Ortiz, 2015; Mora, 2013).
Se prioriza organizar el aprendizaje en pares y grupos, privilegiando la socialización de los sujetos en el qué y cómo aprenden, compartiendo e interactuando en un ambiente social de ayuda mutua desde las experiencias previas (Vygotsky, 1978). Estos presupuestos se han tenido presentes junto a los lineamientos metodológicos de la resolución de problemas desde la metacognición propuestos por Fernández y Aguado (2017), en sus tres momentos: incentivar el conocimiento previo, la reflexión metacognitiva con la presentación de situaciones problemáticas atractivas y retadoras al pensar, y estimular las exigencias intelectuales desde las más sencillas hasta las más complejas.
En el segundo momento, el docente realiza demostraciones y problematiza para inducirlos a que internalicen sus propios procesos cognitivos y así tomen conciencia de cómo aprenden y buscan alternativas para dar solución a los ejercicios planteados. Esta dimensión es denominada control y monitoreo, porque regula el desenvolvimiento de cada acción que debe ejecutarse en el proceso; y el tercer paso corresponde a la evaluación metacognitiva que se da durante todo el proceso de asimilación, comprensión y desarrollo de las actividades para lograr la resolución de la situación problemática.
El docente es un mediador que guía el análisis heurístico y reflexivo en el despliegue de las acciones y procedimientos de la metodología metacognitiva, la aplicación de actividades de aprendizaje variadas con el fin de potenciar la ejercitación de las habilidades de autorregulación, la autoevaluación usando rúbricas como parte del autoconocimiento y las habilidades metacognitivas en la resolución de problemas matemáticos, donde planifican, autocontrolan y autoevalúan su desempeño.
Las estrategias metacognitivas se deben desarrollar teniendo en cuenta las categorías didácticas que se expresan en la Tabla 3.
Las estrategias metacognitivas, como la reflexión y toma de conciencia, están vinculadas con el conocimiento de la persona, la tarea y la estrategia, así como el control de los procesos cognitivos. Durante el proceso de enseñanza-aprendizaje el estudiante realiza acciones específicas, como reflexionar sobre la utilidad de lo aprendido, identificar la información clave y evaluar la relevancia, lo que fomenta un aprendizaje significativo y motiva la participación activa del estudiante en su propio proceso cognitivo.
La estrategia metacognitiva KWL, aplicada al inicio de sesiones de aprendizaje, se relaciona con habilidades como la planificación y autorregulación. El estudiante demuestra habilidades al registrar lo que sabe, expresar sus intereses y objetivos, y agregar nueva información a medida que avanza el curso. Este enfoque fomenta la gestión del aprendizaje, la indagación y la reflexión, lo cual contribuye a un aprendizaje más profundo y significativo.
La estrategia metacognitiva de expresión de emociones, aplicada después de cada ejercicio, se conecta con habilidades metacognitivas, especialmente la evaluación de cada paso individual y en conjunto. El estudiante realiza acciones como relajarse, responder preguntas reflexivas y evaluar aspectos del proceso, lo cual fomenta la autorreflexión emocional y contribuye a un mayor autoconocimiento, con la promoción de un enfoque metacognitivo integral.
Validación de la estrategia metodológica por los expertos
Para validar la efectividad de la propuesta modelada se empleó el método de criterio de expertos. Para ello, se emplearon dos rúbricas orientadas al aspecto externo e interno del producto científico. Como requisitos, este método exigía a los expertos poseer el grado de maestro o doctor en las Ciencias de la Educación y ser especialistas en Matemáticas.
La valoración ofrecida por los expertos fue la siguiente: el especialista 1 dio una valoración total de 89 % considerando la validación interna y externa; el especialista 2, una valoración total de 92 %, y el especialista 3 otorgó un 85 %. Finalmente, la valoración promedio resultante es del 88 %, que se ubica en un valor de muy bueno. En última instancia, los expertos otorgaron la calificación de muy bueno al producto de la investigación. Reconocieron el rigor científico de la propuesta como producto integral, lo cual acredita su aplicabilidad en el proceso de enseñanza-aprendizaje del área de Matemáticas de Educación Secundaria. Añadieron que, por sus fundamentos integrales, el rol del docente y los estudiantes, se convierte en un modelo. Por esta razón, podría generalizarse a otras áreas curriculares del nivel educativo, considerando las características del contexto.
Resultados
Los resultados del trabajo de campo permitieron contrastar la categoría apriorística “resolución de problemas matemáticos” con los datos obtenidos mediante los instrumentos aplicados. En este tipo de estudio, la categoría apriorística es un concepto que se considera independiente de la experiencia empírica y se asume como inherente a priori al conocimiento; es fundamental para organizar y comprender la realidad antes de la experiencia sensorial. Mientras que las categorías emergentes surgen durante el proceso de indagación e interpretación de la información recolectada mediante las técnicas empíricas (Goñi Cruz, 2023). Los datos fueron recopilados de manera simultánea con la aplicación de los diversos instrumentos debidamente validados por criterio de los jueces. Los datos provenientes de la prueba pedagógica fueron procesados estadísticamente por dimensiones y con tres niveles de medición (alto, medio y bajo). En cambio, los datos cualitativos provenientes de la entrevista, observación y el cuestionario de preguntas abiertas fueron analizados cualitativamente; es decir, se llevaron a cabo los procesos de codificación, categorización y triangulación (Hernández et al., 2014; Goñi Cruz, 2023).
Primer momento: reducción de datos y codificación
El proceso de análisis comenzó con la transcripción de las entrevistas grabadas. Posteriormente, se llevó a cabo el proceso manual de codificación de la información obtenida de estas entrevistas, mediante tablas de codificación. Del mismo modo, se realizaron procesos de codificación de la información recabada a través de la observación y del cuestionario de preguntas abiertas. Este proceso de codificación se llevó a cabo mediante un análisis minucioso, palabra por palabra y línea por línea, de toda la información recopilada. Este análisis resultó en la identificación de cientos de códigos, los cuales se utilizaron en el segundo momento de análisis (Goñi Cruz, 2023).
Los resultados de la prueba pedagógica aplicada a los estudiantes evidenciaron el estado de la categoría “resolución de problemas”. A continuación, se presentan estos resultados por dimensiones:
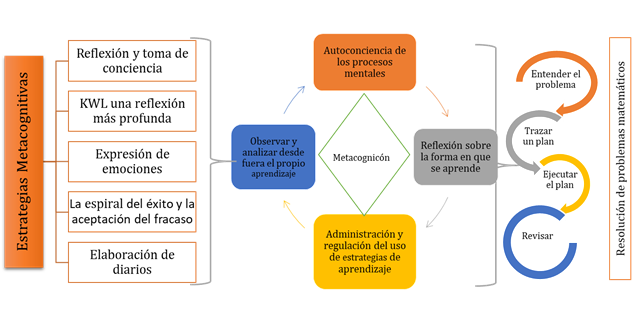
En la dimensión Comprende el problema, el 56.25 % de los estudiantes demostraron un bajo nivel de los conocimientos y las habilidades para resolver las tareas, ya que no identificaron la incógnita, los datos y las condiciones de la tarea a resolver. Se muestran dependientes de la orientación del profesor; el 25 % alcanzó un nivel medio en el dominio de los conocimientos y habilidades necesarias para comprender que les pedía el texto; los estudiantes identificaron la incógnita del problema, los datos y las condiciones de la tarea a realizar e intercambiaron con sus compañeros, aunque con algunas imprecisiones. El 18.75 % alcanzó un alto nivel en el conocimiento y las habilidades al comprender qué pedía el texto; los estudiantes identificaron la incógnita del problema, los datos y las condiciones de la tarea a realizar, e intercambiaron con sus compañeros de manera precisa.
En cuanto a la dimensión Concibe el plan de acciones, el 50 % de los estudiantes evidenciaron un bajo nivel de conocimiento y habilidades, ya que no elaboraron el plan de acciones y relacionaron algunos hechos conocidos por ellos con el problema, aunque no explicaron ni argumentaron sus ideas. El 31.25 % reflejó un nivel medio en los conocimientos y las habilidades al elaborar el plan de acciones, aunque faltaron algunas acciones. Sin embargo, los estudiantes relacionaron bien los hechos conocidos con el problema, explicaron sus ideas y fundamentos. El 18.75 % reflejó un nivel alto en los conocimientos y el desarrollo de las habilidades al elaborar y explicar el plan de acciones; relacionaron bien los hechos conocidos de su contexto con el problema y explicaron detalladamente las ideas del porqué de cada acción.
En la dimensión Ejecuta el plan y examina la solución con visión retrospectiva, el 44 % de los estudiantes evidenciaron un bajo nivel de conocimiento y habilidades al realizar solo una acción del plan orientadas a resolver la tarea hasta su solución. No resolvieron el ejercicio y expresaron que no sabían qué acciones o pasos ejecutar para resolver el problema. El 25 % reflejó un nivel medio en los conocimientos y las habilidades al elaborar el plan y seguir los pasos con cuidado a lo largo del desarrollo hasta su solución y examinar la solución, que es la etapa de la visión retrospectiva; sin embargo, no destacaron qué actividades hicieron, cómo las llevaron a cabo ni verificaron el razonamiento seguido y el resultado final. El 31.25 % demostró un nivel alto en los conocimientos y las habilidades al elaborar el plan, explicar los pasos seguidos en el desarrollo hasta su solución y examinar la solución con autorrevisión de su proceder. Explicaron qué actividades llevaron a cabo, verificaron su razonamiento y analizaron el resultado final. F2
Segundo momento: comparación, relación y clasificación de categorías
Se realizó la comparación, relación y clasificación de los códigos (microcategorías). Este proceso de triangulación permitió la generación de categorías emergentes; es decir, cada categoría emergente fue el resultado de la agrupación de los códigos semejantes. Posteriormente al proceso de la triangulación de los datos, se procedió a redactar las conclusiones aproximativas (memos) para cada categoría emergente, con base en el conjunto de códigos agrupados por su similitud.
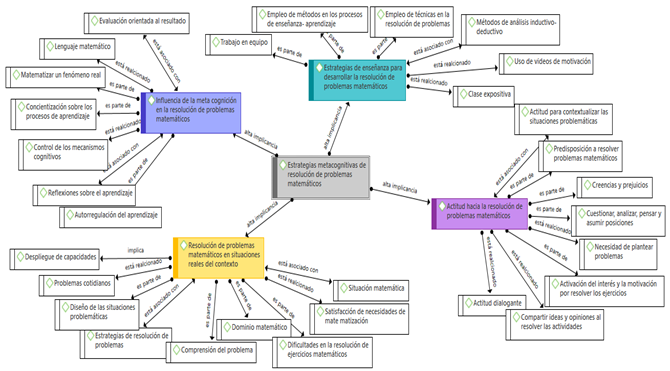
En la Figura 3 se presentan la categoría rectora o eje, las categorías y subcategorías apriorísticas, así como las emergentes que inciden en el problema.
El proceso de categorización se realizó como parte del diagnóstico para conocer el estado de la categoría investigada (resolución de problemas matemáticos) en los niveles teórico y metodológico del proceso de enseñanza-aprendizaje. La aplicación de las técnicas e instrumentos sobre las unidades de observación facilitó la obtención de información, su análisis, interpretación y codificación, para ser contrastarla con las categorías apriorísticas y las emergentes.
Tercer momento: redacción de los hallazgos
En el tercer momento, se procedió a la redacción de los hallazgos encontrados mediante las técnicas aplicadas con el objetivo de identificar las categorías emergentes. Este proceso se llevó a cabo mediante la elaboración de un discurso interpretativo-comprensivo, caracterizado por la crítica y la reflexión entre las informaciones emergentes. Se contrastaron con los referentes teóricos a través de un análisis crítico con el fin de discriminar las categorías emergentes que influyen en el problema investigado y llegar a las conclusiones aproximativas.
Discusión
A continuación, se presenta el análisis de las categorías emergentes influyentes en el problema investigado.
Resolución de problemas matemáticos en situaciones reales del contexto
En esta categoría, los docentes entrevistados manifiestan que para resolver problemas se requiere tener dominio matemático, lo que implica utilizar las capacidades en todo el proceso de enseñanza-aprendizaje. Asimismo, enfatizaron la importancia de generar una reflexión para conocer y resolver problemas que involucren situaciones reales de contexto, con el objetivo de lograr que el estudiante pueda relacionarse con la vida cotidiana y satisfacer las necesidades que se le presenten. Estos resultados son coincidentes a los estudios realizados por Díaz y Careaga (2021), quienes concluyen que es esencial fomentar la conciencia entre profesores y alumnos sobre la resolución de problemas matemáticos en contextos educativos, reconociendo su impacto en la mejora de las prácticas en el aula.
Por otra parte, se observó que la mayoría de los estudiantes no pudieron resolver los ejercicios sobre la solución de problemas, ya que no contaban con las habilidades necesarias; no entendieron lo que les solicitaba el problema, presentando dificultades con la comprensión literal y matemática para saber qué acciones emprender, cómo resolverlo y cómo aplicarlo a la realidad. Enfatizan que la resolución de problemas matemáticos debe partir de un contexto real donde se dan las clases prácticas cotidianas para poder comprenderlo.
En ese sentido se aprecia un doble discurso, pues los profesores coinciden en que los problemas matemáticos deben ser aplicables a la vida real. Sin embargo, al observar las clases, se constató una contradicción entre el discurso y la práctica, evidenciada en la pobre relación que se pretendía hacer entre los problemas analizados con la vida real, al no problematizarse con un sistema de preguntas bien formuladas que oriente a los estudiantes. Por tanto, se evidencian deficiencias didácticas a en el tratamiento del contenido y el diseño de las situaciones problemáticas que no permite a los estudiantes reflexionar, dialogar e interactuar sobre las acciones que deben aplicar para resolver un problema.
Al respecto, se considera que la resolución de problemas es una competencia que exige del educando poner en práctica las experiencias previas, los conocimientos, las capacidades y las acciones para encontrar la respuesta que no conoce. Resolver es saber qué es, comprender, es saber pensar, ejercitar las destrezas y evaluar el proceso desde situaciones concretas del contexto, es decir, aprender matemática en términos de resolución de problemas. En este sentido, Santos (2007) refiere que pensar matemáticamente significa desarrollar un punto de vista que valore el proceso de matematización, abstracción y la tendencia de aplicación; desarrollar una competencia con las herramientas de trabajo, usarlas como meta de comprensión, construir la estructura y desarrollar el sentido matemático.
Enseñanza de la resolución de problemas matemáticos
Esta categoría emergente surge de la información recogida de los diversos informantes de la entrevista y la observación en clase. Se resaltan los diversos problemas que enfrentan los estudiantes, tales como la comprensión inadecuada de textos, manejo inadecuado de técnicas y estrategias de aprendizaje y la falta de motivación por el aprendizaje; frente a ello proponen el empleo de diferentes métodos y técnicas en los procesos de enseñanza-aprendizaje. Uno de los entrevistados resalta el empleo de los métodos de análisis y el inductivo-deductivo para promover el conflicto cognitivo ante un problema como un reto; otro entrevistado propone el trabajo en equipo, donde los estudiantes ponen en acción sus capacidades; ambos coinciden en que el uso de los videos favorece la motivación.
Estos resultados son similares a los que llega Bermeo (2021), quien concluye que la mayoría de los estudiantes enfrenta dificultades en la resolución de problemas matemáticos al depender en gran medida de las operaciones básicas sin un plan definido. La inadecuada comprensión de textos y la falta de verbalización durante la comprensión del problema contribuyen a errores comunes. La escasez de estrategias metacognitivas por parte del docente limita la reflexión del estudiante sobre sus procesos mentales, mientras que la falta de motivación y un estado emocional negativo afectan el aprendizaje, incluso en estudiantes con excelentes capacidades cognitivas. Frente a ello plantea una serie de estrategias activas a emplear durante los procesos de enseñanza-aprendizaje de las matemáticas.
Asimismo, los docentes resaltan que el trabajo en equipo es útil para resolver problemas matemáticos. Sin embargo, la información recogida en el cuestionario a los estudiantes manifestó que los docentes se limitan a realizar la clase expositiva con ejercicios propuestos en la pizarra y entrega de fichas de trabajo para realizarlo en el aula. Asimismo, se observa que tanto la planificación como en la ejecución de las clases son insuficientes en esa dirección, ya que no exigen reflexión, crítica y metacognición; no se vincula el contenido al contexto, el trabajo en grupo ni se potencia el protagonismo de los estudiantes en la apropiación del conocimiento.
Los entrevistados consideran que el proceso de enseñanza-aprendizaje que llevan a cabo sobre la resolución de problemas matemáticos toman en cuenta la competencia matemática y propician el desarrollo de las capacidades, conocimientos y habilidades; es decir, atienden tanto el qué y el cómo resolver problemas a través de diversas situaciones reales del contexto. Sin embargo, en la práctica se constata que no se logra el procedimiento metodológico argumentado por ellos.
En tal sentido, Pérez (2014) y Hernández (2014) refieren la necesidad de que los estudiantes concienticen y perciban el contenido de las matemáticas como una actividad útil, conozcan los procedimientos a seguir y sientan interés por aprender en la clase; deben conocer qué es, cuál es su valor, comprender y su aplicación real en la esfera escolar y en las actividades de la vida cotidiana para que sea un aprendizaje significativo para ellos (Ader, 2019).
La influencia de la metacognición en la resolución de problemas matemáticos
Los hallazgos revelan que en la dirección de la enseñanza-aprendizaje persiste la insuficiencia en la resolución de los problemas. No se tiene claro qué y cómo orientarse hacia un aprendizaje; la evaluación se orienta solo al resultado. No se emplean en la clase procedimientos didácticos que concienticen al estudiantado sobre su pensar ni en lo que aprenden y cómo aprenden. Además, no se aprovechan los saberes previos del contexto para conectar el contenido, ni se utiliza un lenguaje matemático adecuado para matematizar un fenómeno real y demostrarles cómo proceder.
Al respecto, Güner y Nur (2021) manifiestan que resolver problemas matemáticos desde los fundamentos de la metacognición es una actividad cognitiva compleja que involucra múltiples procesos que estimulan el desarrollo del pensamiento, las capacidades y las habilidades en general. En esa línea de ideas, Castellanos et al. (2007) añaden que es el tipo de actividad y sus exigencias las que promueven la observación y el pensamiento crítico de los educandos al resolver los ejercicios en colaboración con otros. Esto les permite desarrollar las habilidades de autoaprendizaje, autoevaluación, ejercitar el aprender a aprender y autorregular su comportamiento (Zimmerman & Schunk, 2000).
Actitud hacia la resolución de problemas matemáticos
Los docentes entrevistados ponen énfasis en la necesidad de plantear problemas y contextualizar situaciones problemáticas significativas, donde se precisen acciones que conduzcan a ejemplificar cómo proceder, en un ambiente de diálogo optimista por vencer obstáculos. De esta manera, se potencie la observación, el interés y la motivación por resolver los ejercicios. En este sentido, se necesario que los estudiantes se sientan orientados, comprendiendo el qué, cuándo, por qué, dónde y cómo utilizar su propio conocimiento al resolver problemas. Esto les provoca una actitud dialogante en la que los estudiantes pueden coincidir, discrepar, ayudarse mutuamente, consensuar y asumir posiciones colectivas hasta alcanzar el objetivo previsto (Mayor, 2009; Donoso et al., 2020).
En este contexto, los estudiantes refieren que resolver problemas matemáticos implica concentración, observación, cuestionamiento, análisis, pensamiento crítico y asumir posiciones. Manifiestan su deseo de que los docentes apliquen metodologías activas, divertidas y participativas al trabajar en equipos con los compañeros, fomentando el intercambio de ideas y opiniones durante la resolución de las actividades. Además, recomiendan que los docentes sean más pacientes al enseñar, ya que muchos estudiantes se ponen nerviosos al no saber cómo abordar las tareas. Otros mencionan que se aburren cuando no comprenden cómo realizar los ejercicios. Sin embargo, también expresan entusiasmo cuando logran resolver los problemas de manera adecuada.
En relación con esto, Ortiz (2015) y Mora (2013) señalan que el sujeto aprende mejor aquello que ama y le interesa, y que la emoción es el ingrediente fundamental para el aprendizaje. Por lo tanto, el aprendizaje será efectivo si se tiene en cuenta la parte afectiva, motivacional y emotiva del educando. Esto significa que cuando el educando recibe una orientación completa, comprende la actividad, reconoce su importancia y despliega sus acciones, se convierte en una fuerza interior que lo estimula, moviliza e interesa por la tarea. Para lograrlo, el docente debe aplicar los métodos problémicos, investigativos, heurísticos y creativos que motiven a los estudiantes y les permitan afrontar nuevos retos, teniendo en cuenta sus necesidades, potencialidades y disposición por aprender.
En ese sentido, el profesionalismo del docente debe propiciar la planificación, el desarrollo y la evaluación de las distintas actividades de enseñanza-aprendizaje. De esta manera, se logra integrar de forma coherente los componentes cognitivos, afectivos, emocionales y motivacionales para generar niveles de interés, emprendimiento, laboriosidad y desarrollo creciente en los estudiantes al realizar actividades basadas en los procedimientos de la metacognición, el autoconocimiento y la autorregulación de sus habilidades. En suma, se requiere que el profesor fortalezca la colaboración y adopte enfoques interdisciplinarios para conducir una enseñanza sostenible que estimule el desarrollo integral para la vida (Deroncele et al., 2023).
Respecto a las actitudes hacia la resolución de problemas, Fernández y Aguado (2017) sostienen que las predisposiciones están mediadas por la valoración y el interés del educando que el docente ha incentivado. Subrayan que es más decisivo el componente afectivo-motivacional que el cognitivo. En este entendido, Vila y Callejo (2005) señalan que, en ocasiones, los estudiantes tienen creencias y prejuicios que pueden tener un poderoso impacto negativo en su aprendizaje. Esto se debe a la manera tradicionalista en que se ha enseñado el contenido matemático, haciendo que los profesores perciban la materia como difícil y rígida, sin contextualizarla en la realidad ni considerar las necesidades de los estudiantes.
Estas creencias se relacionan con ciertas actitudes del estudiante al resolver problemas matemáticos. Algunos encuestados, al plantear la interrogante “¿cómo te sientes al resolver problemas matemáticos?”, respondieron que se sienten un tanto nerviosos porque temen cometer errores, hacer mal los ejercicios y, como consecuencia, obtener una nota deficiente. Esto evidencia una predisposición negativa de inseguridad, ansiedad y atención al resultado más que al proceso de aprendizaje seguido.
Conclusiones
La sistematización de los fundamentos teóricos de la resolución de problemas, entendida como un proceso cognitivo, didáctico y complejo, permitió determinar que la estrategia metacognitiva ayuda a reflexionar, analizar, comprender y recuperar la información como medio potenciador del razonamiento, las habilidades de aprender a aprender, el control y la regulación de los estudiantes al resolver problemas matemáticos.
El uso de los procedimientos metacognitivos, tanto en la etapa de planificación como de monitoreo, regulación, control y autoevaluación del proceso de aprendizaje, orienta, guía y conduce a los estudiantes a la autogestión del conocimiento y, en consecuencia, a producir nuevos conocimientos. Además, fomenta las habilidades intelectuales y las actitudes positivas al enfrentarse a las actividades de solución de problemas desde sus experiencias.
El proceso de triangulación de la información obtenida mediante el diagnóstico de campo demuestra que los docentes presentan deficiencias en la metodología dirigida a potenciar el razonamiento al producir los conocimientos. No se atienden los saberes del contexto ni se crean espacios en la clase para problematizar. Asumir el protagonismo no solo implica conocer los algoritmos al resolver los ejercicios, sino saber aplicarlos en los distintos momentos que requiere resolver un problema de forma metacognitiva.
El proceso de investigación llevado a cabo aporta a la práctica pedagógica, como producto científico, una estrategia metacognitiva que orienta el desempeño del docente en la enseñanza-aprendizaje a fin de potenciar el protagonismo estudiantil en el desarrollo de los conocimientos y las habilidades en la solución de problemas. La evaluación otorgada por los especialistas a la estrategia modelada como resultado del proceso de investigación es positiva, y recomiendan que, por sus fundamentos teóricos y metodológicos, pueda generalizarse a otras áreas curriculares de Secundaria a partir de las características particulares de cada disciplina.
Se enfatiza en la necesidad de continuar la investigación sobre cómo aplicar la evolución metacognitiva en la enseñanza-aprendizaje debido la incidencia positiva de esta en el desarrollo de la independencia cognoscitiva y en la formación integral de los estudiantes de Secundaria.