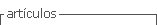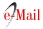Introducción
La literatura sobre resolución de problemas matemáticos ha aumentado considerablemente en los últimos años. El foco ha estado puesto principalmente en el uso de procesos cognitivos, lingüísticos y afectivos que se utilizan a la hora de resolver un problema, y en las acciones, estrategias y procesos heurísticos que deben manejar los estudiantes para el aprendizaje de la matemática escolar (Aguilar, Aragón y Navarro, 2015; Valdés, 2015; Tambychik y Mohd Meerah, 2010). Sin embargo, la evidencia empírica todavía es incipiente en relación a cómo se relacionan los profesores con los estudiantes en las clases de resolución de problemas matemáticos, y especialmente sobre cómo enseñan, qué acciones llevan a cabo, cómo gestionan la participación y cómo utilizan los diferentes momentos de la clase (Hino, 2007). Esto ha implicado que se mire más el aprendizaje y menos la enseñanza, a pesar de ser procesos evidentemente imbricados.
En el caso de Chile, la resolución de problemas es considerada un eje transversal en el curriculum escolar, aspecto que resulta relevante para prestar atención a la enseñanza de las matemáticas y especialmente al abordaje de la resolución de problemas. Según el Ministerio de Educación (2009), la matemática se aprende haciendo matemática, reflexionando acerca de lo hecho y confrontando el conocimiento acumulado con el conocimiento nuevo. Esto interpela directamente a los docentes en su concepción sobre la enseñanza en resolución de problemas, pues los docentes deben generar las oportunidades para que los estudiantes “hagan matemáticas”. Es decir, que aprendan a razonar matemáticamente, entendiendo esto como la capacidad de resolver problemas, formular conjeturas, verificar la validez de procedimientos y razonar bajo hipótesis. Todas estas actividades deberían estar en el núcleo de las experiencias de aprendizaje deseables (Ministerio de Educación, 2009).
Lo anterior nos sitúa en el terreno de la sala de clases y, por lo tanto, en el espacio de la enseñanza, razón por la cual este trabajo se propone caracterizar la interacción entre los procesos de enseñanza y aprendizaje que se establecen entre profesores y estudiantes en las clases de resolución de problemas matemáticos. Los resultados de este estudio responden a una investigación mayor sobre lo que acontece en las aulas cuando los profesores enseñan resolución de problemas matemáticos a los estudiantes.
Las interacciones pedagógicas en el aula
En la década de los 90, en Chile, se crea un proceso de Evaluación Docente con el propósito de fortalecer la profesión y mejorar la calidad de educación. A partir de esta evaluación y de sus múltiples resultados han surgido líneas de investigación que centran su atención en las prácticas que llevan a cabo estos docentes.
Una de estas investigaciones es la realizada por Martinic y Vergara (2007), quienes estudiaron el uso y gestión del tiempo en el aula. Utilizaron clases de profesores de matemática y lenguaje, de 1º a 4º año de Enseñanza Primaria, registradas en video para el Sistema de Evaluación Docente. Estos autores analizaron la relación entre la interacción profesor-alumno y la estructura de la clase. Respecto de la interacción profesor-alumno, observaron que en la clase predomina el habla del profesor, con un estilo de enseñanza que homogeniza a los alumnos, al tiempo que los estudiantes tienen un rol pasivo, interviniendo muy poco durante el desarrollo de la clase. Respecto de la estructura de la clase, encontraron que la mayor parte del tiempo es empleada en el desarrollo, destinando escaso tiempo a los momentos didácticos de inicio y cierre.
Los resultados de este estudio son similares a los obtenidos por Araya y Dartnell (2009), quienes aportaron la caracterización de los patrones de enseñanza de la matemática utilizados por los docentes en sus prácticas pedagógicas, y encontraron diferencias didácticas entre Enseñanza Básica y Educación Media. La investigación arrojó que existen patrones claros de estrategias didácticas que están centradas principalmente en el profesor. Encontraron, además, que existe una dinámica identificable en los momentos didácticos de una clase, reconociendo el inicio, segmentos intermedios y de finalización. En los segmentos intermedios, por su parte, identificaron dos patrones en los profesores, el primero en la línea de la realización de preguntas a los estudiantes y el segundo en la línea de la supervisión del trabajo.
Por su parte, Cornejo, Silva y Olivares (2011) estudiaron el modo en que los profesores presentan contenidos disciplinarios, según el nivel de desempeño obtenido en la Evaluación Docente. Para ello realizaron un estudio centrado en el análisis del carácter interaccional del aprendizaje y la construcción colectiva de un significado entre profesor y alumnos, que abarcó 138 clases de matemáticas de 5° y 6° año de Enseñanza Básica, grabadas en el año 2004. Los autores encontraron que los docentes que obtuvieron buen desempeño recurrían a mayor variedad de formas de presentar los contenidos a sus estudiantes. De igual manera, encontraron que estos docentes recurrían con mayor frecuencia a intervenciones que articulaban dichos contenidos.
Siguiendo la línea de investigación a partir del análisis de los videos de Evaluación Docente, Radovic y Preiss (2010) estudiaron los patrones de discurso presentes en el aula de matemática entre 5º y 8º de Primaria. Los resultados confirmaron los hallazgos de otras investigaciones similares respecto a la identificación de un patrón de interacción en el que predominan las preguntas cerradas con escasa participación de los estudiantes y de bajo potencial metacognitivo.
Para el estudio de la interacción profesor-estudiantes en clases de matemáticas, específicamente en el ámbito de la evaluación de los profesores, se cuenta con instrumentos diversos que pueden ser clasificados en tres tipos: instrumentos basados en la información dada por los propios profesores, protocolos de observación y análisis de productos de las prácticas. Los estudios que surgen a partir del uso de estos instrumentos también aportan resultados de interés para conocer las prácticas que se realizan en el aula. Algunos de estos resultados, respecto de las escuelas con trayectoria de mejoramiento, aportan que los profesores, entre otros, realizan clases más participativas con mayor involucramiento de la perspectiva de los estudiantes, pero con bajo resultado en lo que se refiere a comprensión del contenido y la incorporación del análisis y la indagación, ambas pertenecientes al dominio apoyo pedagógico del instrumento Class1 (Varas, 2016).
En consideración a lo que señala Martínez-Rizo (2012), respecto de que ninguno de estos instrumentos es en sí mismo superior o inferior en comparación con otros, es que se recurre para este trabajo a los aportes de Coll y Sánchez (2008). En la búsqueda de obtener una imagen de la interacción educativa entre profesor y alumnos, estos autores plantean la importancia de otorgar un mayor protagonismo al estudio del discurso que acontece en el aula en el entendido de que proporciona "una mejor comprensión de cómo las personas aprendemos gracias y con la ayuda intencional de otras personas" (Coll y Sánchez, 2008, p. 24).
Coll y Sánchez (2008) aportan, en esta línea, los marcos conceptuales que se utilizan para la observación y análisis de la práctica en el aula. Estos comprenden el uso, por una parte, de modelos cognitivos para el análisis de los contenidos generados mediante la interacción o, por otra parte, el empleo de modelos socioculturales con el propósito de analizar cómo transcurre la interacción en el aula y si está presente un proceso de andamiaje y de apropiación por parte del estudiante durante el proceso. También aplica el uso de ambos modelos, cuando lo que se busca es analizar ambos aspectos en un mismo corpus de datos.
A partir de los resultados y consideraciones antes señalados, se hace necesario profundizar en el tipo de interacción pedagógica que acontece entre profesores y alumnos en las clases de resolución de problemas matemáticos. La intención no es evaluar o comparar estos resultados con el obtenido en la Evaluación Docente, sino identificar, registrar y caracterizar aquellas actividades típicas de aula que favorecen la participación y el aprendizaje de los estudiantes. El reporte focaliza en la resolución de problemas debido a su carácter de dimensión transversal en el currículum escolar chileno y a partir de la necesidad de la literatura especializada de seguir profundizando en esa área.
La enseñanza de la resolución de problemas matemáticos en el aula
Los resultados de evaluaciones nacionales e internacionales han permitido tomar conciencia de la importancia de hacerse cargo de los retos actuales de la matemática escolar (Valdés, 2015), especialmente en el área de la resolución de problemas pues, en el caso de Chile, el currículum contempla entre sus prioridades que esta sea enseñada y diversificada en la sala de clases. Para el caso de este estudio se entiende la resolución de problemas como una descripción de una situación compleja con aspectos indeterminados, cuya resolución requiere de una actividad cognitiva donde se necesita la intervención de procesos personales como autonomía, técnicas y concentración así como procesos y estrategias docentes (Donoso, Valdés, Cisternas y Cáceres, en prensa; Valdés, 2015; González, 2009).
Para algunos estudiantes resolver un problema matemático puede ser un ejercicio simple, mientras que para otros puede ser una tarea difícil o imposible. En ese contexto resulta crucial que los profesores se relacionen correctamente con el estudiantado en el aula y por lo tanto ejerzan procesos variados de enseñanza. Según evidencian los resultados de los instrumentos aplicados a nivel nacional e internacional, los estudiantes chilenos se mantienen mayoritariamente en un nivel insuficiente y elemental de aprendizaje en el área de matemática (Agencia de Calidad de la Educación, 2018). Estos resultados han llevado a investigar la relevancia de propiciar la construcción de modelos matemáticos que favorezcan los aprendizajes en resolución de problemas (Linnenbrink, 2005; Lesh y Zawojewski, 2007). Según Camacho y Santos (2004), es un proceso que demanda examinar rutas potenciales que podrían ayudar o guiar el proceso de construcción del pensamiento matemático de los estudiantes.
En Chile, los estudios de Radovic y Preiss (2010) señalan que la resolución de problemas de manera exitosa requiere, entre otros, del conocimiento de estrategias de resolución, donde el profesor juega un papel relevante en la promoción del conocimiento y actitudes en los estudiantes. Al respecto, Manzi, Preiss, Flotts, González y Sun (2008) señalan que los docentes evaluados con buen desempeño tienen mayor variedad de recursos al momento de presentar los contenidos a sus estudiantes y mayor frecuencia de intervenciones que articulan dichos contenidos. Por su parte, Resnick (1987), Rogoff y Lacasa (1993) y Pozo (1998) se refieren a la importancia que tiene la toma de conciencia de los procesos de aprendizaje y las estrategias para la enseñanza, así como a la búsqueda del cómo construir aprendizajes entre profesor y aprendiz.
Estudios más recientes aportan, además, que las causas de los problemas de comprensión dejan de atribuirse exclusivamente a los alumnos para explicarse desde un punto de vista interactivo (Sixte y Sánchez, 2012). Es decir, si el problema es que los alumnos no extraen las ideas fundamentales para comprender y resolver un problema, el asunto a estudiar no es el alumno, sino el profesor en términos de qué es lo que comunica, cómo lo comunica y qué ayudas ofrece a las comprensiones de los alumnos. Cobra relevancia, en este marco, estudiar la interacción que genera el profesor para guiar el proceso de construcción del pensamiento matemático, ayudando a los alumnos a apropiarse de conocimientos y estrategias. En la medida en que se contribuya a dilucidar lo que acontece en el aula, se estará aportando a la mejora de la interacción discursiva y a las prácticas de enseñanza en la resolución de problemas de enunciado verbal.
La relación entre interacciones pedagógicas y resolución de problemas
Aprender a resolver problemas es un desafío para los estudiantes en los diferentes niveles educativos. El que tengan éxito en la tarea dependerá de conocimientos exclusivamente matemáticos, además de otros conocimientos adquiridos a través de la experiencia, en un aprendizaje continuo que comprende problemas verbales realistas o auténticos que plantean situaciones del mundo real; problemas verbales contextualizados que requieren conocimientos matemáticos, así como el uso de operaciones algebraicas o aritméticas y problemas aritméticos, cuya resolución implica operaciones aritméticas sencillas.
Al respecto, Vicente y Orrantia (2007) plantean que el tipo de tareas que se realizan en el aula y el modo de abordarlas "es, en última instancia, resolver la operación aritmética subyacente (…) y que para ello la única información necesaria es la información matemática" (p. 81). Los autores concluyen que lo anterior podría ser el motivo del bajo rendimiento de los alumnos en problemas similares a los utilizados en el Informe PISA (Agencia de Calidad de la Educación, 2018). De allí la importancia de analizar las interacciones que acontecen en las prácticas de aula desde un enfoque sociocultural, tal como lo plantean Coll y Sánchez (2008).
De acuerdo con lo anterior, las dificultades para el aprendizaje de la matemática y de la resolución de problemas verbales se evidencian a través de los procedimientos y estrategias que utilizan los alumnos para resolver las tareas que se les presentan. El conocimiento de las dificultades en esta área nos permite acercarnos a conocer la manera en que los alumnos reciben e interpretan la información y cómo desarrollan su aprendizaje a partir de los sistemas de interacción que se generan en el aula.
En este sentido los procesos de enseñanza han sido tema de interés para numerosas investigaciones debido al impacto que tiene la enseñanza en los resultados de aprendizaje de los alumnos (Alvarado, Cabezas, Falck y Ortega, 2012; Araya y Dartnell, 2009; Bravo, Falck, González, Manzi, y Peirano, 2008; Manzi, Strasser, San Martín y Contreras, 2008; Lara, Mizala y Repetto, 2010; Olfos, 2010). Específicamente, en el ámbito de cómo se organiza la interacción, Sánchez y Coll (2007) aportan, desde un enfoque sociocultural, un sistema de análisis que permite entender cómo ciertos patrones que organizan el discurso (Indagación-Respuesta-Evaluación) o las actividades (entendidas como episodios tales como lectura e interpretación de la lectura) conforman los aspectos sociales y mentales de los participantes.
Lo anterior se encuentra, a su vez, directamente vinculado al modelo cognitivo en el sentido de qué es lo que se enseña. El modelo cognitivo en este marco aporta los procesos e ideas que son desarrollados o elaborados durante la interacción. A efectos de este estudio, y teniendo como base los aportes de Sánchez, García y Rosales (2010), se precisarán dos conceptos que serán empleados en este trabajo. El primero es el de interacción, entendida como el conjunto de intercambios comunicativos que se suceden entre profesor y alumnos durante el desarrollo de una actividad académica. El segundo es el de patrones, entendidos como los modos de organización de una actividad conjunta entre profesor y alumnos, es decir, las regularidades encontradas en la actividad académica de resolución de problemas matemáticos verbales. Este análisis permitirá describir formalmente lo que acontece en la interacción, desentrañando valores y roles de cada patrón.
Sobre la resolución de problemas, Callejo (1996) aclara que es un proceso que permite al resolutor avanzar en complejidad progresiva. Por otro lado, y enfocado en la forma de desarrollar un problema, Polya (1965) señala cuatro estrategias para la resolución de un problema: comprenderlo, trazar un plan para resolverlo, poner en práctica el plan y comprobar los resultados. Las evidencias que se han desarrollado en posteriores investigaciones apoyan que el elemento discursivo favorece la construcción del modelo de la situación (Thevenot, Devidal, Barrouillet, y Fayol, 2007), lo que significa que el estudiante representa el problema, integrando información del texto con información o conocimiento del lector que está más allá de dicho texto (Sánchez, 2003).
Brissiaud y Sander (2005), por su parte, proponen un marco llamado Situation Strategy First, según el cual ante un problema se construye un modelo que proporciona un tipo de problema llamado solución numérica directa activando estrategias. En este mismo estudio señalan que en problemas en los que no es posible encontrar la solución numérica directa, se recurre a modificar la representación inicial de dicho problema, involucrando con ello recursos cognitivos adicionales como el conocimiento aritmético adicional, el conocimiento conceptual adecuado y la evocación explícita de la operación aritmética.
Por su parte, en Japón, Hino (2007) identifica líneas de investigación que se centran en el comportamiento de los estudiantes en los procesos de resolver problemas en aspectos relacionados con las estructuras, contextos y en relación con las habilidades involucradas en la resolución de problemas. Para ello, busca identificar cómo el profesor guía la atención de los alumnos hacia un aspecto puntual del discurso. A la base de estos estudios se encuentran los aportes de Lemke (1998), quien señala que el aprendizaje va más allá del desarrollo cognitivo autónomo y propone un cambio conceptual en el que el aprendizaje se presenta desde una perspectiva social y es construido a partir de las interacciones entre los profesores, los alumnos, el conocimiento disciplinar y los medios y recursos que el profesor utiliza para la enseñanza.
Estudios que han comparado discusiones dialógicas con formato IRE -estructura conocida como Indagación-Respuesta-Evaluación (Cazden, 1988)- arrojan que los alumnos utilizan más tiempo la palabra y desarrollan las ideas con mayor profundidad cuando la interacción sigue este formato (Reznitskaya y Anderson, 2006). Se observa, además, que los alumnos logran desarrollar habilidades lingüísticas y cognitivas de mayor nivel. Esto se encuentra directamente relacionado con el tipo de preguntas que el profesor elabora para mantener un formato más bien dialógico que interrogativo, fomentando de esta manera mayores posibilidades para que los alumnos desarrollen procesos cognitivos que los lleven a una mejor calidad de la comprensión de lo que acontece en los procesos de enseñanza y aprendizaje (Copeland, 2004).
Por otro lado, Toboso (2005) demostró en un estudio que las habilidades verbales se presentan como un elemento instrumental con incidencia significativa en las restantes habilidades cognitivas que intervienen en el proceso de resolución de problemas matemáticos. Constató que la habilidad para la ejecución algorítmica es la más desarrollada y que las mayores dificultades se presentan en el reconocimiento de la naturaleza del problema -que le da significado y facilita la selección del plan de resolución- así como en la habilidad para organizar las estrategias que ordenan la secuencia de los pasos a seguir. Esta información fue corroborada por Valdés (2015), quien alude al factor de la complejidad de los reactivos en la resolución de problemas. Estudios recientes señalan que los estudiantes menos competentes en matemática muestran un uso poco flexible y a la vez ineficiente del conocimiento conceptual necesario para resolver los problemas aritméticos (Orrantia, Múñez, Fernández y Matilla, 2012).
En el ámbito de la interacción en el aula, la investigación educativa ha contribuido desarrollando formas determinadas de recoger, analizar y estudiar lo que hacen y dicen los profesores y sus alumnos. En esta línea de trabajo se reconoce el aporte de los sistemas de análisis lingüísticos de Sinclair y Coulthard (1975). Posteriormente, surgieron propuestas de corte más psicológico y enfocado en lo que acontece a nivel educativo que aportaron elementos relevantes para una mejor comprensión de las prácticas de aula. En esta línea, un estudio centrado en la interacción en clases de resolución de problemas de matemáticas (Rosales, Orrantia, Vicente y Chamoso, 2008) encontró que los profesores en servicio se aseguran de que los alumnos comprendan el problema antes de seleccionar la operación a realizar, a diferencia de los profesores en formación. Estos últimos tienen prácticas de aula más directivas en los aspectos centrales de la comprensión. Los citados autores utilizan un sistema de análisis que les permite conocer en qué parte del proceso de resolución se centra la interacción y en qué medida se toman las responsabilidades en la construcción de los contenidos que se hacen públicos en dicha interacción.
En un estudio posterior, realizado por el mismo equipo, sobre resolución de problemas en el ámbito de conocimiento conceptual y nivel de competencia en matemática, se señala la importancia que tiene la enseñanza directa y explícita de la forma de enseñar a resolver un problema (Orrantia et al., 2012). Estos dos estudios son de gran importancia para el presente trabajo, por cuanto profundizan en los procesos de enseñanza para el aprendizaje y específicamente en la enseñanza explícita de los pasos a seguir y el modelamiento que realiza el profesor durante los procesos de enseñanza.
Los aportes de estas investigaciones orientan el presente trabajo que, a partir del análisis de registros audiovisuales de clases de matemáticas de centros públicos de enseñanza, intenta responder a la siguiente pregunta: ¿Cuáles son las actividades típicas de aula y los sistemas de participación en las clases de resolución de problemas matemáticos de enunciado verbal entre 5º y 8º año de enseñanza básica?
Metodología
El presente estudio responde a una metodología cualitativa observacional no participativa (Álvarez-Gayou, 2003) con un diseño de serie de casos (Manterola y Otzen, 2014). Consiste en observar, con una pauta de evaluación previamente establecida, comportamientos e interacciones sin tener participación, con el objetivo de recopilar información para luego traducirla en una estructura determinada. Para el caso de este estudio, se crea y se aplica un modelo evaluativo a registros audiovisuales de clases de profesores de matemáticas.
En cuanto a los participantes, estos corresponden a una muestra de 23 profesores de escuelas municipales, evaluados en las clases de matemáticas entre 5° y 8° básico en el proceso de evaluación docente en diversas comunas del país. Se estiman estos cursos por ser una etapa en que se concreta el pensamiento lógico matemático, y los contenidos curriculares de la asignatura se dificultan en complejidad cognitiva. Es decir, los problemas típicos según el currículum escolar en estos niveles deben ser de tipo aritmético, geométrico y con uso de porcentajes y probabilidades. Para el caso de la muestra de este estudio, los problemas matemáticos presentes en las clases fueron mayormente de tipo aritmético (uso de una o más operaciones) y de tipo geométrico (uso de figuras y de fórmulas). No se encontraron problemas sobre porcentajes y probabilidades.
En cuanto a la muestra, el equipo investigador a cargo del estudio solicitó 100 registros audiovisuales de clases de matemáticas entre 5º y 8º básico (25 por curso) al Centro de Perfeccionamiento, Experimentación e Investigaciones Pedagógicas (CPEIP) perteneciente al Ministerio de Educación. Una vez recibidos los registros audiovisuales, se seleccionaron las sesiones que contemplaran como objetivo de la clase el desarrollo de problemas matemáticos. De allí cual quedaron seleccionadas 23 clases para el análisis. Estas corresponden a escuelas de zonas céntricas del país (Región Metropolitana, región de Valparaíso y Región de O’Higgins). Se respetaron los constructos éticos de confiabilidad y responsabilidad exigidos por el CPEIP.
Para este estudio se transcribieron los 23 registros audiovisuales completos, centrando el análisis en el contenido del discurso tanto de profesores como de los alumnos. Del análisis del discurso de las clases transcritas surgen de manera recurrente determinadas actividades donde es posible identificar patrones, los que fueron agrupados teniendo como base el sistema de análisis de Sánchez (1998, 2010) y Sánchez y Coll (2007). Estos patrones fueron organizados en tres ámbitos.
El primer ámbito refiere a los momentos o ciclos que acontecen en las clases, los que en este caso en particular corresponden a inicio -todos los intercambios que acontecen al comienzo de la clase y que culmina cuando se da paso a la resolución de problemas-, desarrollo -todos los intercambios que acontecen durante la resolución de problemas- y cierre de la clase -todos los intercambios que acontecen tras la finalización de la resolución de problemas y que pudieran tener el carácter, entre otros, de resumen, síntesis, valoración o bien explicitación de la finalización de la clase.
En un segundo ámbito se encuentran patrones referidos a actividades típicas de aula (ATA). Para este estudio, estas ATA fueron agrupadas en 11 tipos (Tabla 1), considerando las que emergen desde el inicio hasta el cierre de la clase. En este punto es importante hacer énfasis en que de las transcripciones del discurso de los profesores y de los estudiantes surgen solo 11 actividades típicas, que se encuentran distribuidas en los tres momentos de la clase.
El tercer ámbito focaliza en el tipo de estructura de participación que se establece en el aula. Siguiendo los aportes de las investigaciones de Cazden (1988) y de Reznitskaya y Anderson (2006), estas estructuras se agruparon en cinco tipos (Tabla 2). En este caso es la participación del alumno la que es analizada para dar lugar a la estructura de participación que acontece entre profesor y estudiantes. Cabe aclarar que el sistema de análisis propuesto por Sánchez (1998, 2010) considera la participación autónoma del alumno, pero que en estos registros no acontece, por lo que no se registra (Donoso et al., en prensa).
Tabla 2: Estructuras de participación en clases
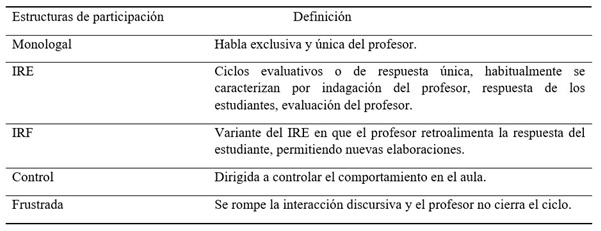
Nota: Elaboración basada en Sánchez y Coll (2007) y en Sinclair y Coulthard (1975).
El procedimiento consistió en analizar tres sesiones de clase, consensuando lo que se entendería por los momentos de la clase y la estructura de participación, para proceder a la identificación de las clases restantes. Una vez llegado a acuerdos en esta etapa, se procedió a la identificación de las ATA y las estructuras de participación. En este punto, nuevamente se planteó una discusión y se llegó a consenso respecto de la interpretación realizada sobre las intervenciones de los profesores y de los alumnos. De esta manera se llegó a identificar las ATA y las estructuras mencionadas.
Luego se realizó una validación de contenido de la pauta creada. Este proceso consistió en que cuatro jueces expertos revisaran las definiciones de las actividades típicas de aula y de las estructuras de participación, coincidiendo en un 98% en la primera y en un 100% en la segunda. Posteriormente, revisaron si estos patrones instruccionales coincidían con las interpretaciones de las clases a las que se había llegado. Este proceso implicó la revisión de dos videos de la misma muestra. Los jueces expertos coincidieron en un 100% en las interpretaciones realizadas sobre la presencia/ausencia de los patrones instruccionales en las clases analizadas.
Finalmente, se aplicaron los modelos antes descritos a las transcripciones de las otras 20 clases grabadas. Este procedimiento fue colectivo y se realizó mediante un trabajo de codificación simple, otorgando a cada momento de la clase las categorías correspondientes a actividades típicas de aula y sistemas de interacción entre estudiantes y profesores.
Resultados
A continuación, se presentan los primeros hallazgos en cuanto a la presencia de las actividades típicas de aula por cada momento de la clase y se establecen las estructuras de participación presentes en las clases de resolución de problemas. Conjuntamente, se agregan citas textuales de las actividades más y menos presentes en las figuras, para ejemplificar los discursos e interacciones.
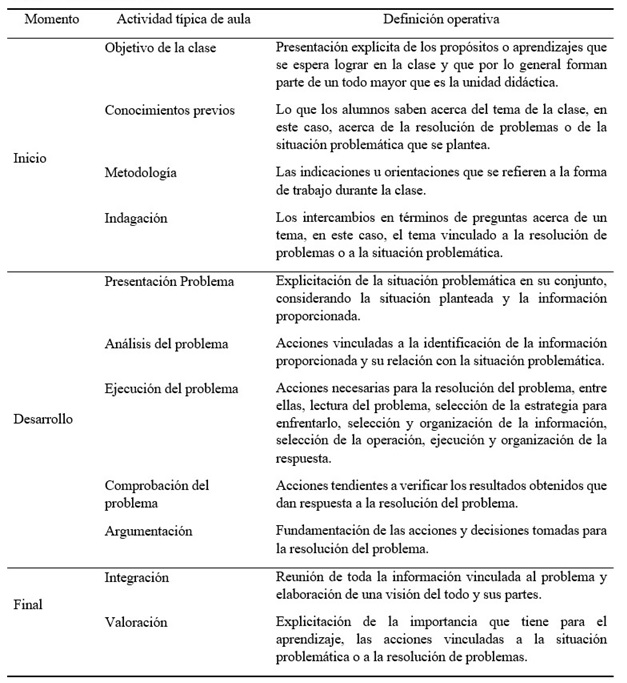
La Figura 1 evidencia los resultados de la presencia de las actividades típicas de aula durante las clases de los 23 profesores durante el momento de inicio.
Se evidencia que, si bien prácticamente todos los profesores activan conocimientos previos en el inicio, 16 de ellos precisan la metodología que utilizarán los estudiantes para lograr los propósitos de la clase. Esto quiere decir que 16 docentes expresan a sus estudiantes el cómo alcanzarán ese objetivo que fue explicitado en el mismo momento de la clase.
Consiguientemente, la mayoría de los docentes realiza preguntas exploratorias con diferentes motivos pedagógicos. Se destaca, además, que un grupo de profesores no explicita los objetivos de la clase o los aprendizajes que se espera logren los alumnos. Respecto del inicio de la clase, entonces, la actividad que todos los profesores realizan es la activación de conocimientos previos.
Un ejemplo de activación de conocimientos previos (ATA más frecuente) es la siguiente cita de uno de los profesores de las clases analizadas:
Antes de empezar tenemos que recordar un poquitito lo que hemos estudiado del lenguaje algebraico. Dijimos nosotros que el lenguaje algebraico uno lo puede expresar a través de números, letras, ¿no es cierto?, una información dada, se puede expresar más que nada una información dada.
En relación con las actividades menos presentes, aparecen la precisión de la metodología a utilizar en la clase y la indagación mediante preguntas exploratorias. A continuación, se especifica una cita de la primera:
El segundo momento, vamos a trabajar desarrollando una clase práctica trabajada en grupo en que, eehh… vamos a trabajar con una situación que vamos a conocer a don Pedro para calcular el área. Y, por último, al final, van a salir a exponer su trabajo y a autoevaluarse.
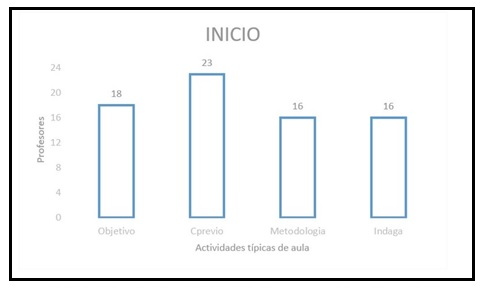
En la Figura 2, en el desarrollo de la clase, se puede visualizar que la mayor parte de los profesores presentan el problema a desarrollar durante la clase, es decir, lo leen -de forma unívoca o en conjunto- a sus estudiantes, lo analizan y lo ejecutan.
No obstante, a medida que avanza el momento de la clase, las actividades de mayor complejidad cognitiva se van haciendo menos presentes, siendo las actividades de comprobación y argumentación las que se encuentran entre las actividades que realiza el 65 y 60%. Según plantea Pozo (1998), uno de los elementos centrales en los procesos de enseñanza es hacer explícito el conocimiento implícito, para ello la argumentación juega un papel esencial y en este caso no es un elemento que esté presente en todas las clases.
Siendo la presentación del problema la actividad más frecuente, evidenciamos una cita que ejemplifica dicha ATA en el desarrollo de la clase:
Profesora: Aquí está el problema, ¿alguien que lo quiera leer?
Alumno: En una carrera de revés Martin corrió 1/5 de un kilómetro de la carrera y Susana corrió 1/3 de kilómetros. ¿Quién corrió más? ¿Cuánto más?
Profesora: Yo quiero saber si alguien se atreve a resolverlo. Ahí está el problema, léalo y resuélvalo, tienen dos minutos, vamos a ver si son capaces de resolverlo.
En cuanto a la argumentación (ATA menos frecuente), a continuación, una cita que ejemplifica lo realizado por una profesora de 8º básico:
Profesora: Mire, ¿por qué podrá salir dos veces el 0? Empezó primero el 0 con 8. El 0 de x ¿y el 8 de... ? Más porque va a caer en el mismo punto, ¿para qué?
Alumna: Para que se pueda cerrar.
Profesora: Para que se cierre la figura. Pasen lo mismo con el cuerpo del monito y también pasa lo mismo con los ojos ¿ya? Si se equivocan no importa ¿ya?
En la Figura 3, y en cuanto al cierre de la clase, un 39% de los profesores integraron lo visto en la clase y un 43% valoraron lo trabajado durante la sesión de matemáticas.
Es importante destacar que este momento de la clase estuvo marcado por la presencia solamente de estas dos actividades, es decir, las clases por lo general no presentaron cierre y, si lo hubo, las únicas actividades presentes fueron integración de contenidos y su valoración. En el caso de la integración de contenidos, a continuación, se expone una cita representativa:
Esto por favor que nos quede claro, para poder resolver cualquier problema yo tengo que leer bien y de ahí para todo. Si yo leo bien voy a resolver cualquier problema que me ponga y sobre todo cuando son ecuaciones inmediatamente fijarme cuando no me dan el número inmediatamente, sé que es una incógnita, vuelvo a repetirles la incógnita puede ser cualquier letra.
En el caso de la valoración de contenidos, a continuación, se presenta una cita ilustrativa de una clase de una profesora que, durante el cierre, les otorga un valor práctico a las matemáticas:
Muy bien, nos sirve para la vida cotidiana, cada día las matemáticas son muy importantes para nuestra vida. Yo los felicito porque hicieron un buen trabajo. ¿Qué fue lo que les costó más? ¿Cuál ejercicio?
La Figura 4 explicita las estructuras de participación entre profesores y estudiantes en el proceso de enseñanza y aprendizaje.
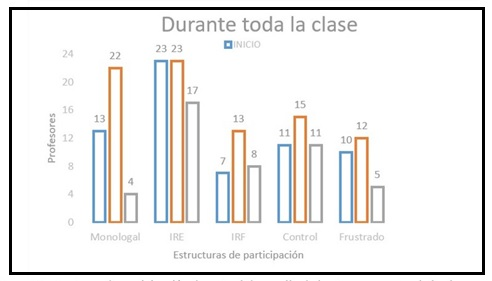
Figura 4: Fuente: Estructuras de participación durante el desarrollo de los tres momentos de la clase
Los principales resultados muestran que las estructuras monologales e IRE están mayormente presentes durante las sesiones, mientras que el IRF se encuentra en menor cantidad. Por otro lado, las estructuras de control y frustrada también poseen una presencia importante durante los tres momentos, especialmente en el desarrollo y cierre de la clase. Esto implica que las pautas de interacción entre docente-alumno están siendo marcadas principalmente por oralidades exclusivas del docente.
En cuanto a los estudiantes, estos presentan un protagonismo más limitado durante la clase y sus intervenciones son más bien breves. Un ejemplo de IRF, una de las actividades de aula que más interesa pero que no es frecuente, es la siguiente:
Profesora: El total de las dos divisiones juntas me dio 15 ¿Y qué número falta ahí arriba?
Alumna: Tres.
Profesora: ¿El tres por qué?, ahí tres pintados del total de 15, ¿verdad? ¿Y aquí qué falta?
Alumna: El cinco.
Profesora: ¿Por qué el cinco?
Alumna: Porque cinco están pintados.
Profesora: Entonces cómo quedaría la respuesta ¿quién corrió más?
Alumna: Susana.
Profesora: Susana, ¿y cuánto más?
Alumna: 2/15
Profesora: Excelente.
Discusión y reflexiones finales
El objetivo de este estudio fue caracterizar la interacción entre los procesos de enseñanza y aprendizaje que se establecen entre profesores y estudiantes en las clases de resolución de problemas matemáticos. Si bien los primeros resultados son incipientes y la investigación aún está en curso, ya se pueden analizar algunos hallazgos que, si bien no son generalizables, sí resultan bastante sugerentes. El análisis se centró en las actividades típicas de aula de los profesores de matemáticas durante los tres momentos de las clases y en las estructuras de participación durante el proceso de enseñanza.
Los resultados arrojan que un número importante de profesores enuncia el objetivo a desarrollar en la clase, no obstante, durante el desarrollo no se hace alusión a dicho objetivo para orientar el trabajo que se está realizando o para focalizar la actividad en base a una meta específica. Otro resultado importante es que, si bien los profesores en el inicio de la clase realizan una activación de los conocimientos previos, durante el desarrollo no plantean preguntas vinculadas al objetivo para favorecer la construcción del modelo de la situación (Thevenot et al., 2007) que le permite al alumno representar la situación problemática e integrar la información con el conocimiento que posee.
El profesor no evidencia realizar un seguimiento al proceso de comprensión del estudiante antes de dar paso a la resolución (Rosales et al., 2008). Se manifiestan interacciones centradas en el docente y en la oralidad del proceso que este va ejecutando. Una de las aspiraciones de los profesores es que los estudiantes avancen en autonomía pero, para ello, es imprescindible compartir los significados (Sánchez, 2010; Rosales et al., 2008) identificando o volviendo sobre el objetivo al momento de identificar el problema, al analizar las alternativas de resolución (Callejo, 1996; Polya, 1965) o bien al momento de realizar el cierre de lo trabajado en la clase. Recurrir al objetivo permite el monitoreo y el seguimiento de la actividad que se realiza en relación con la autorregulación del aprendizaje (Hino, 2007).
Otro de los resultados que llama la atención es el desarrollo de habilidades cognitivas superiores como la argumentación (Toboso, 2005), durante el desarrollo de la clase a partir de los resultados obtenidos y durante el cierre con la integración de las ideas. En ambas situaciones no se da espacio a trabajar el reconocimiento de la naturaleza del problema, lo que incide en otorgarle significado y a su vez facilita -en la medida que se aprende- a la selección del plan de resolución y a organizar las estrategias que ordenan la secuencia de los pasos a seguir.
La ausencia de estas actividades en las clases analizadas lleva a preguntar cuál es el aprendizaje que se obtiene tras el ejercicio de resolución del problema, si el análisis fue escaso y la integración de las ideas también lo fue. Esto se vuelve un asunto especial si se consideran los aportes de la literatura respecto de procesos cognitivos y los contenidos que se generan en la interacción, así como la apropiación que se hace de estos (Coll y Solé, 2001; Sánchez, 1998, 2010; Goizueta y Planas, 2013), y estudios en esta misma línea que comprenden desde la educación infantil a la enseñanza superior en lo que se refiere a los grados de transferencia (Cubero, 2005).
Siguiendo la línea anterior, resulta relevante mencionar el sistema de interacción que genera el profesor con los alumnos. Los ciclos de interacción, independientemente del nivel de curso o la cantidad de alumnos, muestran que los profesores mantienen estructuras de participación de tipo monologal, es decir, es el profesor el que tiene la mayor participación en la clase. Ocurre lo mismo para el caso de los IRE (indagación, respuesta y evaluación), en donde también predomina una enseñanza monologal a pesar de que los profesores de la muestra realicen preguntas. Estos sistemas de interacción se mantienen incluso al momento del cierre de la clase, en el que es el profesor el que lidera la participación.
Bajo esta modalidad, se está lejos de la perspectiva social de la construcción del conocimiento a partir de las interacciones que se generan entre el profesor, los alumnos, el conocimiento disciplinar y los recursos que se utilizan para la enseñanza (Lemke, 1998). La participación -conforme arroja este estudio- se reduce principalmente a la participación del profesor y a una escasa incidencia de los alumnos. El profesor no genera las instancias para la participación de los alumnos, como sería, por ejemplo, el planteamiento de preguntas como plantean Thevenot et al. (2007).
Estos resultados, aunque incipientes, permiten focalizar la atención en las prácticas de aula y en la formación inicial de profesores en lo que se refiere a interacciones pedagógicas. El análisis cualitativo de la información arrojó datos relevantes para reflexionar acerca de la forma en que se realizan las clases y lo que puede ser factible de mejorar en lo que se refiere a patrones de interacción profesor-alumno, haciendo uso de actividades típicas e intencionadas en los momentos de inicio, desarrollo y cierre de una clase.
Para cerrar, es necesario señalar que, en la medida en que los profesores realicen actividades de mayor complejidad en el aula, hay mayores posibilidades para que los estudiantes adquieran estrategias para resolver los problemas matemáticos que se esperan en el curriculum escolar (Ministerio de Educación, 2009). Uno de los desafíos es, entonces, continuar investigando en la resolución de problemas aplicado a distintas ATA y en diferentes niveles de curso, edad y asignaturas.