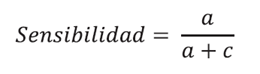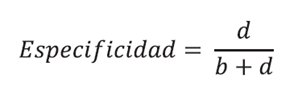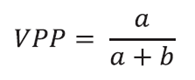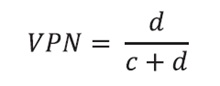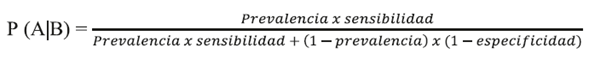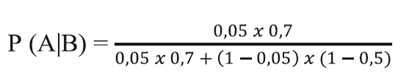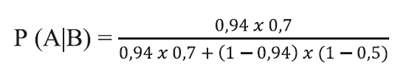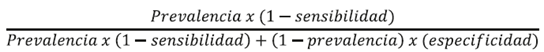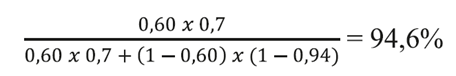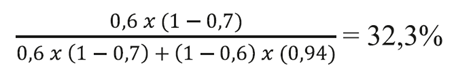Utilidad de los estudios diagnósticos

Los estudios diagnósticos tienen como finalidad poder definir la probabilidad de padecer una enfermedad, tanto en pacientes asintomáticos (tamizaje o screening) como en pacientes sintomáticos. Dentro de las primeras enseñanzas que recibimos cuando entramos en Facultad de Medicina es que los estudios diagnósticos se solicitan con la intención de, en primer lugar, definir, con “el menor error posible”, un diagnóstico determinado, para, en segundo lugar, poder implementar una intervención terapéutica que permita mejorar la calidad de vida y/o prolongar la sobrevida del paciente.

Pensemos este escenario de la forma siguiente: cuando nos enfrentamos por primera vez a un paciente, la realidad está ahí delante de nuestros ojos, el paciente tiene o no tiene la enfermedad. Aquí no hay probabilidades, la certeza está delante de nosotros, el problema es que esa certeza, en ese preciso momento, nos es desconocida. Y de eso se trata gran parte de la práctica de la medicina: desarrollar una serie de estrategias (obteniendo datos a partir de la anamnesis, el examen físico, la aplicación de estudios paraclínicos, sumados a una serie de conocimientos epidemiológicos sobre la enfermedad en cuestión) para reducir al máximo posible la incertidumbre diagnóstica, y así reducir al máximo el error diagnóstico.

Utilidad de los estudios diagnósticos para definir la probabilidad de una enfermedad

El estudio diagnóstico ideal es aquel que siempre será positivo en aquellos pacientes con la enfermedad y que siempre será negativo en aquellos sin la enfermedad, esto es, que confirme la presencia de la enfermedad en todos los enfermos y la descarte en todos los sanos. En términos técnicos, esto sería un estudio con una sensibilidad del 100% y una especificidad del 100%, respectivamente. Por desgracia, esta situación ideal casi no se da en la práctica habitual. Pero para definir qué tan preciso y válido es un test diagnóstico debemos compararlo con algo. Ese algo es la referencia o patrón oro (gold estándar) en la determinación de la enfermedad. Para el caso del cáncer, por ejemplo, el gold estándar es la biopsia y la interpretación de su anatomía patológica (aclaremos que esto último es discutido para algunos tipos de cáncer). Para el caso de la enfermedad arterial coronaria (EAC) que podría afectar a Juan, en cambio, el gold estándar es la coronariografía o la angiotomografía coronaria multicorte.

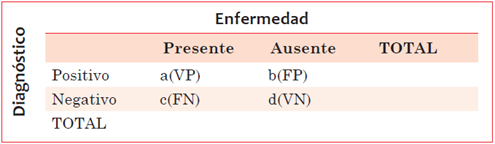
Para determinar los criterios de validez y predicción de los estudios diagnósticos, es de gran utilidad analizar los posibles resultados en una tabla de 2 × 2 como la que se muestra en la figura 1.

Figura 1.  Tabla de resumen diagnóstico. La sensibilidad (S) y la especificidad (E) se calculan de forma vertical en la tabla, mientras que los valores predictivos se hacen de forma horizontal. VP: verdadero positivo; FP: falso positivo; FN: falso negativo; VN: verdadero negativo 

Sensibilidad (S)

La S es la probabilidad de diagnosticar la enfermedad en aquellos sujetos que sí tienen la enfermedad. Por tanto, su cálculo se basa en el total de diagnósticos positivos de los pacientes que tienen la enfermedad, de acuerdo con la siguiente fórmula, referida a la tabla de la figura 1 como:

Así, cuanto mayor es la S del test diagnóstico, mayor es la probabilidad de detectar los pacientes con la enfermedad. Por lo tanto, un resultado obtenido por un test con alta sensibilidad es suficiente para excluir la presencia de enfermedad (en caso de ser negativo), pero no para confirmar su presencia (en caso de ser positivo)”. Imagínense que intentamos pescar tiburones con una red de mojarritas. Cuando hacemos esto, podemos estar seguros de que no habrá tiburones que no hayamos atrapado. Sin embargo, no podemos afirmar que todos los que levantemos en la red sean tiburones, pues hay peces (grandes, pero no tiburones) que queden atrapados en la red. Volvamos al caso de Juan. Aunque estemos cansados y sea nuestro último paciente de la policlínica, la situación bien merece aguzar nuestro razonamiento clínico. La ergometría convencional o test ECG de esfuerzo tiene una sensibilidad del 70% para el diagnóstico de EAC. Eso quiere decir que, de 100 pacientes con EAC, la ergometría será positiva en 70 de ellos. Dicho de otra manera, habrá 30 pacientes portadores de EAC en los cuales el test diagnóstico será negativo. Estos se denominan resultados falsos negativos (FN) de la ergometría y su cálculo deriva de: 1 − sensibilidad. Si, en cambio, la S de la prueba fuera del 100%, el test sería capaz de detectar a todos aquellos con EAC, por lo que con un resultado negativo uno podría estar muy seguro de que no tendría EAC (FN = 0).

Ahora, imaginemos algo descabellado, pero útil: que nuestro test diagnóstico para EAC consiste solo en saber la edad del paciente. La evidencia disponible al momento ha permitido definir que el test da positivo si la edad es mayor a 18 años. Este tendrá una sensibilidad del 100%, o sea, será excelente para excluir a los que no tienen EAC. Pero ¿es esto suficiente para decir que todos los pacientes mayores de 18 años tienen EAC? Como se habrán imaginado, no lo es y, por lo tanto, es necesario saber cuántos de los resultados que se informan como positivos son realmente positivos, y no falsos positivos (FP). (cuantos peces levantados como tiburones en realidad no lo son)

Especificidad (E)

La especificidad (E) es la probabilidad de excluir la enfermedad en aquellos que no tienen la enfermedad (sanos). Su cálculo se basa en el total de los diagnósticos negativos en los pacientes que no tienen la enfermedad, mediante:

Asumimos que la E de la ergometría es del 50%. Esto quiere decir que, de 100 pacientes sin EAC, el resul tado será negativo en 50 de ellos. Pero también quie re decir que los otros 50 serán positivos a pesar de no tener EAC. Estos resultados se denominan falsos po sitivos (FP) y su cálculo deriva de: 1 − especificidad. Observemos que cuanto mayor es la E de un test diag nóstico (menos FP) mayor será la posibilidad de in cluir efectivamente como enfermos a aquellos que no tienen la enfermedad (sanos). Un resultado positivo de un test que tiene 100% de E (sin FP) nos confirma que el individuo tiene la enfermedad. Resumiendo lo antedicho, si queremos excluir la enfermedad busca remos un test con alta sensibilidad, mientras que si queremos confirmar la enfermedad, buscaremos un test con alta especificidad (tabla 1).

Esto subraya el concepto de que, antes de solicitar un estudio, el clínico debe siempre preguntarse: “¿pará que quiero la prueba en este caso particular?”, lo cual no siempre significa (ni siempre es posible) contar con un test que demuestre muy alta S y muy alta E.

^{Tabla 1.} Tipo de test diagnóstico según objetivo.

Es muy común que confundamos los significados de la S y la E de un test diagnóstico. Es útil imaginarse que la S y la E son índices que caracterizan el rendimiento diagnóstico en forma análoga a lo que hacen la visión panorámica y la visión de alta magnificación de un microscopio o cámara fotográfica, respectivamente. Imaginemos que miramos un monte para identificar los robles, confundiéndolos lo menos posible con otras especies de árboles. Si estoy interesado en ver el porcentaje de robles que existen en el monte, podré hacerlo a través de una vista panorámica, sabiendo que al mirar de lejos podré incurrir en el error de incluir otros tipos de árboles como robles (falsos positivos, como alerces o pinos, por ejemplo). Cuanto más panorámica la vista, mayor será la S, esto es, mayor será la probabilidad de identificar los robles en el monte. Pero si miro el monte con una cámara de alta magnificación (alta E), que me permite ver a nivel milimétrico, existe el riesgo de que excluya a los que son robles por no ver la totalidad del árbol y solo sus hojas (falsos negativos). De esta forma podemos comprender que cuanto más sensible sea un estudio (menos zoom) mayor será la probabilidad de tener falsos positivos, y que cuanto más específico sea (más zoom) mayor la probabilidad de tener falsos negativos. Volviendo al ejemplo de la red de pesca, cuanto más chicos sean los agujeros del entramado (mayor S) mayor será la probabilidad de pescar tiburones (menos FN), pero también de levantar mojarritas (mayor FP). Cuanto más ajustado el tamaño de los agujeros al tamaño medio de los tiburones (mayor E), menor será la probabilidad de levantar tiburones (mayor FN) y menor la de levantar mojarritas (menor FP). Por lo tanto, la S y la E de un test diagnóstico dependerá solo de las características intrínsecas del test, del zoom y los megapíxeles de la cámara, o del tamaño de los agujeros en la red de pesca, en cada uno de nuestros ejemplos.

^{Tabla 2.} Riesgo de falsos positivos y negativos de acuerdo con la sensibilidad y la especificidad del test diagnóstico.

Una vez llegado a este punto, creemos conveniente hacer algunas apreciaciones. Los conceptos de S y E de un test aluden a la capacidad propia del test, a lo que el test vale por sí mismo (también llamada capacidad intrínseca). Estas características no deberían variar en ninguna circunstancia, siempre y cuando, por supuesto, contemos con un test con buena reproducibilidad o confiabilidad. Un problema especial surge cuando el resultado del test es observador-dependiente. En esta situación, la S y la E cambian en función de quien lo aplica, lo que, obviamente, complejiza mucho más las cosas. Otro aspecto crucial es que, como se mencionó anteriormente, ambos índices (S y E) se obtienen comparando el rendimiento del test en una muestra de pacientes con y sin la enfermedad en cuestión considerando un test patrón oro. Aquí surgen dos consideraciones: por un lado, la muestra (n) de individuos con la enfermedad debería haber sido aplicada a una muestra aleatoria y representativa del universo (N) de individuos con la enfermedad (y en el caso de que no fuera así, debería aclararse a qué subgrupo o estrato se le aplicó) y, lo que no es menos importante, en el grupo de individuos sin la enfermedad se debió también aplicar a una muestra aleatoria y representativa del universo de individuos sin la enfermedad. Por otro lado, está la cuestión de la disponibilidad de un patrón oro. En efecto, este a veces existe (lo que evidentemente simplifica y facilita las cosas), pero otras veces no existe o es inaplicable (sobran ejemplos, aunque por razones de extensión no abundaremos sobre ello). En este último escenario, en el que no hay un patrón oro sobre el cual comparar, podemos intentar construir un algoritmo para aproximarnos a este, como podría ser la sumatoria de varios tests aplicados en forma paralela o sucesiva, o la comparación con la opinión de un grupo de expertos, por ejemplo, pero siempre teniendo la precaución de no incluir el test estudiado en este algoritmo diagnóstico. Por último, el lector atento se habrá percatado de que todos los conceptos vertidos hasta ahora implican que el test diagnóstico en estudio provea un resultado dicotómico: positivo o negativo. Otra situación diferente se plantea cuando el resultado se expresa mediante una variable cuantitativa. Un ejemplo clásico es el de la cifra de glicemia obtenida en condiciones de ayuno. Pensemos que podríamos fijar diferentes puntos de corte para definir una glicemia alterada (por ejemplo, 1,10, 1,20, 1,30, 1,40 g/litro). En este caso, queda muy evidente la relación inversa entre S y E: a medida que aumento mi punto de corte aumenta la E y disminuye la S. Sucede exactamente lo inverso si elijo puntos de corte con valores menores. Profundizar sobre estos conceptos implicaría incursionar en los conceptos de calibración y discriminación (curvas ROC), lo cual no es el objetivo del presente artículo.

Valores predictivos

El valor predictivo de un test diagnóstico, como su nombre lo indica, nos dice qué valor tiene el test para predecir la presencia o ausencia de la enfermedad. Ese valor se mide en porcentajes y es, en definitiva, lo que le importa al paciente y lo que debemos comunicarle a Juan; son los argumentos para tomar una decisión, también llamados capacidad extrínseca de un test. El valor predictivo positivo (VPP) nos informa acerca de la probabilidad de tener la enfermedad cuando el test diagnóstico es positivo:

El valor predictivo negativo (VPN), en cambio, nos informa acerca de la probabilidad de no tener la enfermedad cuando el test diagnóstico resulta negativo:

Veamos dos ejemplos simples y teóricos.

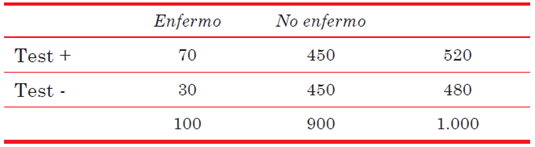
Ejemplo 1:  Test A en una población con una prevalencia del 10% (100/1000). Sensibilidad (S) = 70/100 = 70% Especificidad (E) = 450/900 = 50% VPP = 70/520 = 13,5% VPN = 450/480 = 94% 

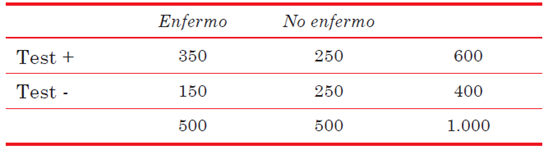
Ejemplo 2:  test A en una población con una prevalen cia del 50%. Sensibilidad (S) = 350/500 = 70% Especificidad (E) = 250/500 = 50% VPP = 350/600 = 58,3% VPN = 250/400 = 62,5% 

Enfoque bayesiano del problema

En realidad, lo que Juan quería saber en el consultorio era cuál era el VPP de la ergometría que realizó. Para poder entender el cálculo de este, integrándolo directamente con la prevalencia de la enfermedad, es necesario realizar una reseña al teorema de Bayes. Thomas Bayes fue un reverendo presbiteriano del siglo XVIII. Nacido en Londres y miembro de la Royal Society, tenía un especial interés por el cálculo de la probabilidad. Como era un teólogo, ideó una estrategia para estimar la probabilidad de que Dios existiera, incorporando en esa estrategia (o teorema) la evidencia previa (o creencia) que había sobre dicha existencia. Así, la estadística bayesiana incorporó la experiencia previa en la predicción del evento. De acuerdo con la inferencia bayesiana, si tiro una moneda 100 veces y obtengo 86 caras, la probabilidad de obtener cara al lanzarla otra vez no es 0,5, sino mayor, dado que incorpora la experiencia previa, según la cual la probabilidad de obtener cara es de 0,86. El teorema de Bayes, que se aplica al tema que nos convoca (y al caso de Juan), permite establecer la probabilidad de un evento A dado B sabiendo la probabilidad de B dado A. En otras palabras, si conocemos cuál es la probabilidad de B conociendo A desde antes, el teorema de Bayes nos permite saber la probabilidad de A sabiendo B. Traspolando estos conceptos a los tests diagnósticos, el teorema de Bayes permite calcular el valor predictivo que se atribuye a un resultado positivo de cierta prueba diagnóstica en función de las características intrínsecas de dicha prueba (su S y su E) y también de la prevalencia de la enfermedad. Así, se transforma o modifica la probabilidad a priori (pretest), representada por su prevalencia, en la probabilidad a posteriori o postest (valor predictivo), una vez observado un resultado (positivo) de la prueba diagnóstica.

Volviendo a nuestro ejemplo, si sabemos cuál es la probabilidad de tener una ergometría positiva en los pacientes con EAC, el teorema de Bayes nos permitiría saber la probabilidad de tener EAC frente a un resultado positivo de la ergometría. Dicho teorema se encuentra en el núcleo de las decisiones terapéuticas que se desprenden de todos los estudios diagnósticos que diariamente guían nuestra acción médica. Como médico y cardiólogo, son pocas las fórmulas que debemos tener dentro de nuestra memoria (anatómica o digital). Consideramos que la fórmula del teorema de Bayes, expresada a continuación, es una de ellas.

P (A|B) = P (B|A) P (A) / P (B).

Donde:

P (A): probabilidad del evento A.

P (B): probabilidad del evento B.

P (A|B): probabilidad del evento A sabiendo que B es verdadero.

P (B|A): probabilidad del evento B sabiendo que A es verdadero.

En nuestro ejemplo, la probabilidad del evento A se refiere a la prevalencia de EAC (probabilidad de tener EAC o pretest). La probabilidad del evento B, en cambio, se refiere a la probabilidad de tener una ergometría positiva. P (A|B) es la probabilidad de tener EAC dada una ergometría positiva, y P (B|A) es la probabilidad de tener una ergometría positiva en un paciente con EAC (sensibilidad). Para poder entender cómo se derivan los números resultantes, pongamos como ejemplo lo que ocurriría en una población con 10.000 habitantes (sabiendo que la probabilidad de que un individuo adquiera EAC es de 7% en individuos mayores de 20 años) que se someten a un estudio ergométrico con la sensibilidad descrita al inicio. Los resultados se expresan en la tabla 3.

^{Tabla 3.}

En negrita se muestran los valores que se logran ingresar en la tabla diagnóstica a partir de los datos proporcionados de S, FP y prevalencia (P). Con los datos de la tabla, podemos fácilmente calcular cuál es la probabilidad de tener una ergometría positiva, mediante: P (B) = 5.140 / 10.000 = 0,514. Y también podemos calcular la probabilidad de que, frente a una ergometría positiva, Juan realmente tenga una EAC.

P (A|B) = (0,7 × 0,07) / 0,514 = 0,095

Otra forma de expresar esta fórmula sin necesidad de armar una tabla diagnóstica es la siguiente:

En otras palabras, de cada 10 individuos con ergometría positiva, solo 1 tendrá EAC. Este valor es el VPP. En casos en los que contamos con una tabla diagnóstica como la anterior, el VPP puede calcularse simplemente como:

Total de EAC con ergometrías positivas / total de ergometrías positivas. En nuestro ejemplo, el VPP será: 490 / 5.140 = 0,095%

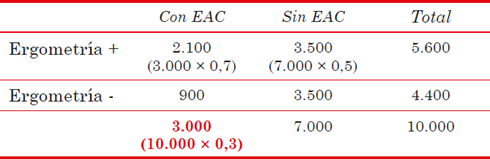
Ahora imaginemos que Juan se muda a Infartópolis, un país imaginario con una alta prevalencia de EAC (30%). Juan se somete al mismo estudio ergométrico (en condiciones similares) y consulta a su médico luego del resultado positivo. ¿Cuál sería la probabilidad de que Juan tenga EAC con este resultado positivo (VPP) obtenido en Infartópolis? Para esto, construimos la siguiente tabla de 2 × 2:

Entonces, la probabilidad de que Juan tenga EAC en Infartópolis es casi 4 veces mayor que en Uruguay. Por lo tanto, si queremos disminuir el riesgo de que Juan tenga EAC, digámosle… que se mude a un sitio con baja prevalencia (en Marte la prevalencia es 0%).

Probabilidad pre y postest

Como mencionamos, el objetivo de un test diagnóstico es ayudar al clínico a definir la presencia o ausencia de una enfermedad en cuestión. La validez del test, entonces, se centra en qué tan fuerte puede apoyar la decisión de confirmar o excluir la presencia de la enfermedad.

Probabilidad pretest

Consiste en la probabilidad de tener la enfermedad previo a la realización del estudio diagnóstico. Como vimos, de forma general la probabilidad global de tener EAC está representada por la prevalencia. Sin embargo, el riesgo varía según las características clínicas del paciente, y dicho riesgo deberá ser individualizado durante el cálculo. Existen varias tablas que estiman el riesgo de enfermedad de acuerdo con ciertas características clínicas (en general unas pocas). En estos casos, el riesgo de enfermedad en el individuo bajo estudio pasaría a sustituir a la prevalencia durante los cálculos de probabilidad postest. Así, por ejemplo, alguna de estas tablas nos dice que un hombre de 30 años, deportista, no fumador, con valores normales de glicemia en ayunas y un perfil lipídico normal tendrá una probabilidad pretest muy baja de padecer EAC.

Para definir la necesidad de realizar un estudio diagnóstico, Straus y col. sugiere tomar dos referencias¹: una probabilidad pretest baja (como el caso anterior de Juan) y una probabilidad pretest alta (hombre de 75 años, fumador intenso, diabético, hipertenso con historia de ángor típico de 3 meses de evolución). La utilidad de realizar estudios diagnósticos es mayor en aquellos pacientes con una probabilidad pretest intermedia.

Probabilidad postest

En 1979, Diamond y Forrester definieron la probabilidad pretest de EAC en una gran muestra de pacientes con base en el tipo de dolor, la edad y el sexo (solo 3 variables, dos categóricas y una dicotómica)². Pero volvamos, entonces, al caso de Juan. La probabilidad pretest de que Juan tenga EAC (considerando que está asintomático) estaría en torno al 5%. Al subirlo a la bicicleta ergométrica y someterlo a un protocolo de esfuerzo que sea adecuado a su estado clínico, obtenemos un resultado positivo. Usando los conceptos vertidos anteriormente, calculamos cuál es la probabilidad de que Juan tenga EAC, mediante la fórmula:

Para el segundo caso (hombre de 75 años, fumador intenso, diabético, hipertenso con historia de ángor tí pico), la probabilidad pretest estaría en torno a 94%.

Entonces, de ser negativa la ergometría, la probabilidad de tener EAC sería de 90,4%.

Como vemos, la utilidad clínica de realizar un test diagnóstico en un individuo con probabilidad pretest muy elevada o muy baja es escasa, dado que, sea cual sea el resultado, este impacta muy poco sobre la probabilidad postest.

En aquellos casos en los cuales la probabilidad postest de EAC es intermedia (por ejemplo, 60%), la ergometría no es suficiente para confirmar el diagnóstico o descartarlo, para lo que es necesario realizar estudios adicionales. En estos casos, la probabilidad pretest del nuevo estudio diagnóstico es la misma que la postest del estudio anterior (60%). Para agregar mayor complejidad aún, recordemos que las probabilidades pretest pueden cambiar de acuerdo con el momento y la región. En efecto, los algoritmos de estimación de la probabilidad pretest de EAC actuales estiman probabilidades bastante menores que los anteriores como el de Diamond y Forrester en todas sus categorías. Además, los nuevos algoritmos permiten ser aplicados en sujetos con edades mayores y en pacientes que se presentan con disnea³.

Veamos otro ejemplo, el de la paciente María. Luego de realizarse una ergometría, calculamos que la probabilidad postest para EAC de María se encuentra en torno al 60%. Considerando que el riesgo de EAC de María es intermedio, y no suficiente como para proceder a una angiografía coronaria (estudio invasivo, no exento de riesgos) que permita confirmar o descartar el diagnóstico de EAC. El cardiólogo tratante decide realizar un centellograma de perfusión con Talio, el cual tiene una S de 70% y una E de 94% para el diagnóstico de EAC frente a hallazgos de isquemia reversible. Frente a un resultado positivo, la probabilidad postest de EAC sería:

El problema del sesgo de referencia

El sesgo se define como una diferencia sistemática en una medida que la aparta del valor real. Para profundizar sobre el tema de los sesgos relativos a las pruebas diagnósticas recomendamos al lector referirse a Mower WR y col.⁴.

Uno de los sesgos más frecuentes en la práctica clínica y que aplica al caso de Juan es el denominado sesgo de referencia o sesgo de derivación. Este sesgo resulta de realizar el test gold standard solo en aquellos pacientes cuyo resultado del test en cuestión sea positivo. Intentando resumir la situación (y a riesgo de ser reduccionista), solo en caso de que la ergometría de Juan fuera positiva es que Juan será derivado a un cateterismo. Así, en la práctica clínica real la gran mayoría de las derivaciones a cateterismo provienen de resultados anormales en una prueba no invasiva como la PEG o el centellograma de perfusión miocárdica, por ejemplo. En consecuencia, muchos más pacientes con resultados positivos de la prueba de evaluación de isquemia no invasiva serán remitidos para angiografía coronaria que aquellos pacientes con resultados negativos. De esta manera, la casilla de la tabla de contingencia 2 × 2 correspondiente a los FN captará mucho menos pacientes y, en consecuencia, la E termina siendo subvalorada. Una de las estrategias dirigidas a atacar el problema es calcular otros índices, alternativos a la especificidad, que permitan atenuar dicho sesgo. El más utilizado de ellos es la denominada tasa de normalidad (originalmente del término en inglés normalcy rate). En nuestro ejemplo de Juan, la tasa de normalidad se define como el porcentaje de pacientes que tienen una baja probabilidad pretest de EAC (< 5%) en los que se obtienen resultados normales en el mismo período de estudio. Estos pacientes se asumen como los más probablemente negativos, aun cuando no sean derivados al test patrón oro (angiografía), y se integran en la casilla de la tabla de 2 × 2 de la figura 1 correspondiente a los FN, corrigiendo el valor previo de E⁵. Desgraciadamente, son pocos los estudios de evaluación diagnóstica que, en un intento por atenuar el sesgo de referencia, reportan índices como la tasa de normalidad.

La precisión diagnóstica

Finalmente, queremos hacer algunas consideraciones sobre el concepto de exactitud o precisión diagnóstica (originalmente del término en inglés diagnostic accuracy). En términos generales (y semánticos), los índices ya descritos (S, E, VPP, VPN) son todos parámetros que cuantifican la propia exactitud de una prueba. Algunos autores, sin embargo, utilizan el término precisión diagnóstica (o efectividad diagnóstica) expresándola como la proporción de los sujetos que son clasificados correctamente (VP + VN) dividida entre todos los sujetos (VP + VN + FP + FN)⁶. Como ya se explicó, esta precisión diagnóstica se ve afectada por la prevalencia de la enfermedad. Así, la precisión diagnóstica de una determinada prueba aumentará a medida que disminuye la prevalencia de la enfermedad. Sin embargo, esto no significa que la prueba sea mejor o más exacta si la aplicamos en una población con baja o alta prevalencia de la enfermedad, sino que solo significa que en número absoluto la prueba provee más sujetos correctamente clasificados. Además, este porcentaje de sujetos correctamente clasificados debe sopesarse siempre considerando otras medidas de precisión diagnóstica, en especial los valores predictivos ya descritos. Otros autores, en cambio, simplemente realizan un promedio de la S, la E, el VPP y el VPN para expresar la precisión diagnóstica, en un intento por resumir las propiedades de la prueba con un solo índice.

Conclusiones

Como hemos intentado ilustrar, la correcta selección e interpretación de los estudios diagnósticos para EAC en el caso de Juan adquiere un gran valor para decidir sobre la conducta futura. Su valor radica en las características intrínsecas del test (como la S y la E), pero también en la prevalencia de la enfermedad (probabilidad pretest o prevalencia). Es primordial que el clínico incorpore estos conceptos en su práctica clínica diaria, en un intento por optimizar la eficiencia de los estudios diagnósticos, evitar gastos innecesarios, sobrediagnósticos y complicaciones.