Servicios Personalizados
Revista
Articulo
Links relacionados
Compartir
CLEI Electronic Journal
versión On-line ISSN 0717-5000
CLEIej vol.19 no.1 Montevideo abr. 2016
Balancing Energy and Performance
in Dense Linear System Solvers
for Hybrid ARM+GPU platforms
Abstract
The high performance computing community has traditionally focused uniquely on the reduction of execution time, though in the last years, the optimization of energy consumption has become a main issue. A reduction of energy usage without a degradation of performance requires the adoption of energy-efficient hardware platforms accompanied by the development of energy-aware algorithms and computational kernels. The solution of linear systems is a key operation for many scientific and engineering problems. Its relevance has motivated an important amount of work, and consequently, it is possible to find high performance solvers for a wide variety of hardware platforms. In this work, we aim to develop a high performance and energy-efficient linear system solver. In particular, we develop two solvers for a low-power CPU-GPU platform, the NVIDIA Jetson TK1. These solvers implement the Gauss-Huard algorithm yielding an efficient usage of the target hardware as well as an efficient memory access. The experimental evaluation shows that the novel proposal reports important savings in both time and energy-consumption when compared with the state-of-the-art solvers of the platform.
Abstract in Spanish
La comunidad de computación de alto desempeño (HPC del inglés) tradicionalmente se ha focalizado únicamente en la reducción de los tiempos de ejecución, sin embargo, en los últimos años, la optimización del consumo energético se ha convertido en un tema importante. La reducción en el uso de energía sin una pérdida de desempeño requiere la adopción de hardware eficiente desde el punto de vista energético, acompañado también del desarrollo de algoritmos que consideren este aspecto. La resolución de sistemas lineales es una operación clave en diversos problemas relacionados con la computación científica. Su relevancia ha motivado un volumen importante de trabajo y, en consecuencia, es posible encontrar resolutores que incluyen técnicas de HPC para una amplia gama de plataformas de hardware. En este trabajo, se avanza en el desarrollo de variantes para la resolución de sistemas lineales que incluyen técnicas de computación de alto desempeño y contemplan aspectos energéticos. En particular, se desarrollan dos resolutores para una plataforma híbrida CPU+GPU de bajo consumo, la Jetson TK1 de NVIDIA. Estos resolutores implementan el método de Gauss-Huard, buscando hacer un uso eficiente de la plataforma de hardware objetivo, considerando las características de su jerarquía de memoria. La evaluación experimental muestra que la novel propuesta reporta importantes reducciones tanto en el tiempo de ejecución como en el consumo energético cuando se compara con el estado del arte en resolutores para dicha plataforma.
Keywords: Dense Linear Systems, Gauss-Huard, NVIDIA Jetson K1, Energy-aware computing
Keywords in Spanish: Sistemas lineales densos, Gauss-Huard, Jetson K1 de NVIDIA, Computación considerando asepctos energéticos
Received: 2015-12-13 Revised: 2016-02-17 Accepted: 2016-02-17
DOI: http://dx.doi.org/10.19153/cleiej.19.1.2
1 Introduction
The solution of a system of linear equations of the form
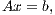 | (1) |
where 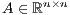 is a dense matrix, and
is a dense matrix, and 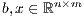 represent respectively, the right-hand side vector of independent terms (RHS) and the sought-after solution, is the main computational problem in the solution of many scientific and engineering applications [1]. The traditional method to solve a general linear system is based on the LU factorization (i.e., Gaussian elimination), which must be complemented with (partial) row pivoting to ensure numerical stability [2]. The operation involves the factorization of the matrix
represent respectively, the right-hand side vector of independent terms (RHS) and the sought-after solution, is the main computational problem in the solution of many scientific and engineering applications [1]. The traditional method to solve a general linear system is based on the LU factorization (i.e., Gaussian elimination), which must be complemented with (partial) row pivoting to ensure numerical stability [2]. The operation involves the factorization of the matrix 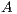 into the lower-triangular matrix
into the lower-triangular matrix 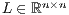 and the upper-triangular matrix
and the upper-triangular matrix 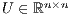 such that
such that 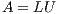 . Then,
. Then, 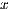 is obtained via the solution of two triangular linear systems:
is obtained via the solution of two triangular linear systems: 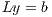 and
and 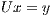 . The factorization stage is the most time consuming operation of the process, and involves about
. The factorization stage is the most time consuming operation of the process, and involves about 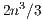 floating-point arithmetic operations (flops), in contrast with the
floating-point arithmetic operations (flops), in contrast with the 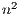 flops of each subsequent triangular solver. The factorization phase and, therefore, the most time-consuming part of the method, can be expressed in terms of BLAS-3 operations [3]. Thus, an efficient implementation of this method on a parallel platform can potentially deliver remarkable performance. As a consequence, this is the method implemented in the LAPACK library (routine gesv), as well as in MATLAB® (command linsolve or backslash).
flops of each subsequent triangular solver. The factorization phase and, therefore, the most time-consuming part of the method, can be expressed in terms of BLAS-3 operations [3]. Thus, an efficient implementation of this method on a parallel platform can potentially deliver remarkable performance. As a consequence, this is the method implemented in the LAPACK library (routine gesv), as well as in MATLAB® (command linsolve or backslash).
The Gauss-Jordan elimination (GJE) is an efficient algorithm to compute the matrix inverse, and can be easily adapted to obtain the solution of linear systems of equations. The numerical stability can also be improved via partial pivoting. The main interest in this algorithm lies in its high degree of parallelism and its reduced number of memory operations. Consequently, this method usually delivers remarkable efficiency in modern hardware architectures that present a large number of computational units [4, 5]. However, when applied to the solution of linear systems, GJE incurs a larger computational cost than the traditional approach based on the LU factorization. In particular, it requires 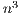 flops, compared with the
flops, compared with the 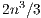 flops of the LU-based method. This limitation makes it useless as soon as the dimension of the system (
flops of the LU-based method. This limitation makes it useless as soon as the dimension of the system (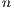 ) becomes moderate. In the late 70s, P. Huard presented the Gauss-Huard algorithm (GH) [6], which can be considered as an extension of the GJE algorithm for the solution of linear systems, and represents an alternative and reliable method when complemented with column pivoting [7]. Interestingly, this method presents the same computational cost as the LU-based solver, i.e.,
) becomes moderate. In the late 70s, P. Huard presented the Gauss-Huard algorithm (GH) [6], which can be considered as an extension of the GJE algorithm for the solution of linear systems, and represents an alternative and reliable method when complemented with column pivoting [7]. Interestingly, this method presents the same computational cost as the LU-based solver, i.e., 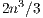 flops.
flops.
In recent years, hardware architectures have experienced remarkable changes. Mainly motivated by the limitations on power consumption, the strategy of increasing the processor frequency has been replaced by an increment in the number of computational units. GPUs and the Intel Xeon Phi processors are successful exponents of this trend. These new hardware platforms offer from tens to thousands of computational units, and are more energy-efficient than traditional multi-core processors. In this domain, the solutions presented by NVIDIA that integrate in a single board a low power ARM processor and a GPU occupy a relevant position. In particular, the most important example of this type of platforms is the NVIDIA Jetson TK1, composed of a quad-core ARM Cortex A15 processor and a Kepler GPU with 192 CUDA cores. However, to fully exploit the capabilities of these new platforms, the methods and their implementations must be reformulated.
This work aims to obtain a high-performance and energy-efficient linear system solver based on the Gauss-Huard method (with partial column pivoting) optimized for the NVIDIA Jetson TK1. We extend the work in [8] to further improve the new solvers and evaluate their performances in terms of runtime, but also energy. We include in the evaluation the state-of-the-art solvers in ARM and hybrid CPU-GPU platforms, specifically OpenBlas [9] and MAGMA [10]. Our experimental results show that one of the new implementations outperforms, in both runtime and energy consumption, the solvers included in the previous libraries, for problems of moderate to large dimensions (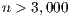 ).
).
The rest of the paper is structured as follows: In Section 2, we describe three methods for the solution of linear systems based on the LU factorization, the GJE based strategy and the GH algorithm. Then, in Section 3, we present two new GPU-based versions that implement the GH algorithm, this is followed by an experimental evaluation of their performance and energy efficiency in Section 4. Finally, we discuss some conclusions and future work in Section 5.
2 Dense linear systems resolution
In this section, we revisit different approaches to compute the solution of a dense linear system 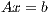 with dense
with dense 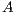 . In numerical linear algebra (NLA), there are two main families of methods to solve this kind of problems: direct and iterative methods; see [2]. The first family consists of by deterministic methods that compute the exact solution of the problem (neglecting unavoidable floating-point rounding errors). On the other hand, iterative methods start with an initial solution and, after successive approximations, converge to a solution according to certain criteria. This usually means that a threshold, tol, is set such that when the difference between the computed solution and the exact solution is lower than tol, the method stops. From the computational point of view, direct methods generally present a computational cost of
. In numerical linear algebra (NLA), there are two main families of methods to solve this kind of problems: direct and iterative methods; see [2]. The first family consists of by deterministic methods that compute the exact solution of the problem (neglecting unavoidable floating-point rounding errors). On the other hand, iterative methods start with an initial solution and, after successive approximations, converge to a solution according to certain criteria. This usually means that a threshold, tol, is set such that when the difference between the computed solution and the exact solution is lower than tol, the method stops. From the computational point of view, direct methods generally present a computational cost of 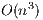 flops and are mostly based on BLAS-3 operations, allowing an efficient use of the memory hierarchy in modern hardware platforms. In contrast, iterative methods present a computational cost of
flops and are mostly based on BLAS-3 operations, allowing an efficient use of the memory hierarchy in modern hardware platforms. In contrast, iterative methods present a computational cost of 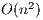 flops per iteration and they do not take advantage of BLAS-3 operations which limits their performance. However, an iterative method may be faster than a direct method if it presents a lower computational cost, namely, the number of iterations is considerably smaller than
flops per iteration and they do not take advantage of BLAS-3 operations which limits their performance. However, an iterative method may be faster than a direct method if it presents a lower computational cost, namely, the number of iterations is considerably smaller than 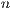 (i.e., the convergence is fast or the problem does not require a high accuracy in the solution). On the other hand, direct methods allow to reuse most of the computations in the successive solution of linear systems with the same coefficient matrix. In this work, we focus on direct methods for the solution of dense linear systems. In more detail, in this section we describe three direct approaches based on the traditional LU, the GJE and the GH algorithms. All methods are in-place and, therefore, present a similar cost in terms of memory requirements.
(i.e., the convergence is fast or the problem does not require a high accuracy in the solution). On the other hand, direct methods allow to reuse most of the computations in the successive solution of linear systems with the same coefficient matrix. In this work, we focus on direct methods for the solution of dense linear systems. In more detail, in this section we describe three direct approaches based on the traditional LU, the GJE and the GH algorithms. All methods are in-place and, therefore, present a similar cost in terms of memory requirements.
2.1 Solution of linear systems via the LU factorization
The LU-based algorithm for the solution of linear systems is analogous to the traditional strategy based on Gaussian elimination. Specifically, the method consists of three steps that initially (first step) compute the 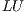 factorization of
factorization of 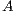 . This operation requires of a row pivoting strategy to ensure numerical stability [2]. The decomposition takes the form
. This operation requires of a row pivoting strategy to ensure numerical stability [2]. The decomposition takes the form 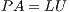 , where
, where 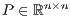 is a permutation matrix, and the factors
is a permutation matrix, and the factors 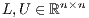 are, respectively, unit lower triangular and upper triangular. The
are, respectively, unit lower triangular and upper triangular. The 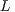 and
and 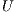 factors are stored in the memory space of
factors are stored in the memory space of 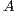 (i.e. in-place) to reduce the memory requirements. The main diagonal of
(i.e. in-place) to reduce the memory requirements. The main diagonal of 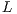 does not need to be stored since
does not need to be stored since 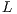 is unit lower triangular. To further reduce memory use,
is unit lower triangular. To further reduce memory use, 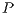 is implicitly stored as a vector. Then, the system is rewritten as
is implicitly stored as a vector. Then, the system is rewritten as 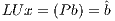 and, therefore,
and, therefore, 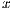 can be obtained by solving the triangular linear systems
can be obtained by solving the triangular linear systems 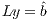 followed by
followed by 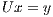 .
.

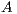 . Upon completion,
. Upon completion, 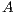 is overwriten by the triangular factors
is overwriten by the triangular factors 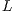 and
and 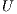 .
.

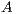 . Upon completion,
. Upon completion, 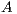 is overwriten by the triangular factors
is overwriten by the triangular factors 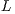 and
and 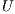 .
. Most of the computational cost is due to the factorization of 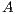 . This can be exploited when several systems involving the same coefficient matrix must be solved. In this case, the factors
. This can be exploited when several systems involving the same coefficient matrix must be solved. In this case, the factors 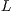 and
and 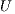 can be reused while the matrix decomposition needs to be computed only once. Consequently, the solution of the successive systems presents a computational cost of
can be reused while the matrix decomposition needs to be computed only once. Consequently, the solution of the successive systems presents a computational cost of 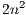 flops. Figure 1 shows an in-place unblocked variant of the Gaussian elimination algorithm to compute the LU factorization using the FLAME notation [11, 12]. In the figure,
flops. Figure 1 shows an in-place unblocked variant of the Gaussian elimination algorithm to compute the LU factorization using the FLAME notation [11, 12]. In the figure, 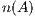 stands for the number of columns of
stands for the number of columns of 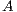 .
.
Figure 2 shows the blocked version of the method, where 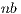 is the algorithmic block size. For simplicity, pivoting is not included in both algorithms. In general, blocked variants tend to offer better performance in modern hardware architectures, since they improve the computational intensity [2] and reduce the memory operations.
is the algorithmic block size. For simplicity, pivoting is not included in both algorithms. In general, blocked variants tend to offer better performance in modern hardware architectures, since they improve the computational intensity [2] and reduce the memory operations.
The LU-based method presents some drawbacks that limit its performance on massively parallel architectures. Concretely:
- The method consists of three sequential stages (LU factorization, upper triangular solve and lower triangular solve), implicitly defining two synchronization points.
- In addition, it requires the solution of two triangular linear systems, an operation that presents a rich collection of data dependencies and limited concurrency. Furthermore, small triangular linear systems also appear during the factorization stage.
These problems present little relevance when the dimension of 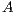 grows, since the factorization concentrates most of the computational effort. In this situation, the possibility to use BLAS-3 kernels during the factorization turns the method extremely suitable for parallel platforms.
grows, since the factorization concentrates most of the computational effort. In this situation, the possibility to use BLAS-3 kernels during the factorization turns the method extremely suitable for parallel platforms.
LAPACK [13] is a specification that provides many important NLA operations, and offers high performance and numerically reliable implementations for many types of platforms. Certain implementations may include a number of high performance computing (HPC) techniques and also particular customizations for different processors and architectures. The LAPACK specification includes support for the different stages of the LU-based solver. In particular, the routine getrf computes the LU factorization (applying partial row pivoting) of a non-singular matrix, while the routine getrs allows the solution of the subsequent triangular systems from the factors computed by getrf. Additionally, LAPACK includes the gesv driver routine for the solution of linear systems, which simply performs the appropriate calls to the routines getrf and getrs.
2.2 The Gauss-Jordan method
An alternative method for the solution of dense linear systems is the so-called Gauss-Jordan Elimination method (GJE). This algorithm calculates the inverse of a matrix, but can be easily adapted to obtain the solution of a linear system. Additionally, if row pivoting is employed, the algorithm exhibits stability properties similar to those of the Gaussian Elimination method [14].
The solution of linear systems with this method implies the application of GJE to the extended matrix ![Aˆ= [A,b]](/img/revistas/cleiej/v19n1/1a0253x.png) . The method processes the extended matrix from left to right, updating, at each iteration, all the entries of
. The method processes the extended matrix from left to right, updating, at each iteration, all the entries of 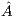 . For the solution of linear systems, only the elements to the right of the active column need be updated, reducing the computational cost to
. For the solution of linear systems, only the elements to the right of the active column need be updated, reducing the computational cost to 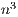 flops. Once the process is completed, the solution of the linear system (i.e., the
flops. Once the process is completed, the solution of the linear system (i.e., the 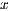 vector) is stored in the last column of the extended matrix
vector) is stored in the last column of the extended matrix 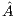 .
.
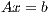 . Initially,
. Initially, ![Aˆ= [A,b]](/img/revistas/cleiej/v19n1/1a0259x.png) . Upon completion, the solution
. Upon completion, the solution 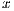 overwrites the last column of
overwrites the last column of 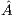 .
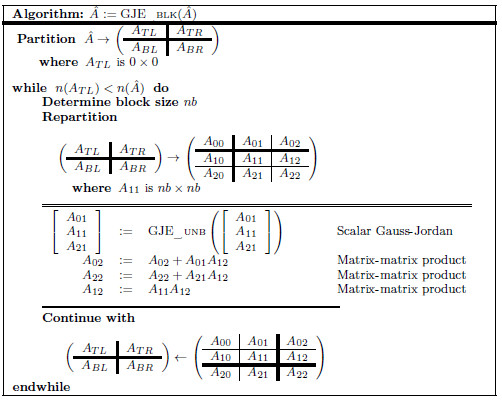
. Figure 3 shows the blocked version of the GJE to solve the linear system of equations associated with 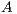 . For simplicity we do not include pivoting in the description. A description of a scalar version of the GJE method, that is invoked in the blocked version, can be found in [15]. It should be noted that this is also an in-place method, which means that, when the process is completed, the matrix
. For simplicity we do not include pivoting in the description. A description of a scalar version of the GJE method, that is invoked in the blocked version, can be found in [15]. It should be noted that this is also an in-place method, which means that, when the process is completed, the matrix 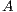 is overwritten with the transformed matrix and
is overwritten with the transformed matrix and 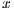 overwrites
overwrites 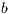 (in the last column of
(in the last column of 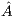 ).
).
This method is rich in BLAS-3 operations. In particular, the updates 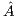 are performed via matrix-matrix products. This usually yields a high throughput when executed on massively parallel platforms. On the other hand, the use of the GJE method to solve a linear system requires
are performed via matrix-matrix products. This usually yields a high throughput when executed on massively parallel platforms. On the other hand, the use of the GJE method to solve a linear system requires 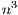 flops, in contrast to the
flops, in contrast to the 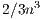 flops for the LU-based method. In consequence, this method cannot compete with the LU-based algorithm for the solution of systems of large dimension.
flops for the LU-based method. In consequence, this method cannot compete with the LU-based algorithm for the solution of systems of large dimension.
2.3 The Gauss-Huard method
As previously stated, the GJE method presents some features that turn it especially appealing for its implementation on massively parallel platforms. Unfortunately the algorithm also presents a high computational cost for the solution of linear systems of equations compared with the LU-based method. This drawback was addressed by P. Huard [6] in the late 1970s. In his work, he presents a smart variant of the GJE algorithm to solve linear systems that incurs a computational cost analogous to that of the LU-based method. This method, known as the Gauss-Huard (GH) algorithm, presents a convenient memory access pattern. But this feature is destroyed if row pivoting is introduced to ensure numerical stability. This problem was overcome by T. J. Dekker et al. in [16, 7]. They proposed the inclusion of column pivoting and proved that the resulting method offers numerical characteristics similar to those of the LU factorization with row pivoting.

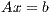 . Initially,
. Initially, ![ˆA = [A, b]](/img/revistas/cleiej/v19n1/1a0271x.png) . Upon completion, the solution
. Upon completion, the solution 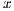 overwrites the last column of
overwrites the last column of 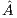 .
. Figure 4 describes the GH for the solution of a linear system of equations. Pivoting is not included in the algorithm for simplicity, although all our variants integrate partial column pivoting. In practice, pivoting can be easily added as follows: before the diagonalization of ![[ ] ˆα11, ˆaT12](/img/revistas/cleiej/v19n1/1a0274x.png) , this vector is searched for its maximum entry in magnitude (excluding its last element, which corresponds to an entry of
, this vector is searched for its maximum entry in magnitude (excluding its last element, which corresponds to an entry of 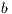 ) and the column of
) and the column of 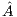 corresponding to this entry is then swapped with the column of
corresponding to this entry is then swapped with the column of 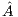 containing the diagonal entry
containing the diagonal entry 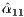 .
.

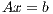 . Initially,
. Initially, ![Aˆ= [A,b]](/img/revistas/cleiej/v19n1/1a0280x.png) . Upon completion, the solution
. Upon completion, the solution 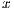 overwrites the last column of
overwrites the last column of 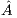 .
. A blocked variant of GH was introduced for distributed-memory (message-passing) systems in [17]. Unfortunately, the authors did not perform any experimental evaluation of the implementation, and simply stated that its performance could be expected to be close to that of an LU-based solver.
Figure 5 describes a blocked version of the Gauss-Huard algorithm which processes 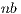 columns of the matrix per iteration.
columns of the matrix per iteration.
3 Gauss-Huard implementations for hybrid CPU-GPU platforms
CPU-GPU platforms have currently reached a prominent position in HPC, as revealed by the top positions of the Top500 list [18]. They are also widely used in the domain of numerical methods and linear algebra. This is reflected by the efforts integrated in modern scientific numerical libraries to exploit this kind of platforms; see e.g., MAGMA [19], PETSc [20] or ViennaCL [21]. All those libraries include routines to solve (dense and sparse) linear systems taking advantage of the capabilities provided by this kind of hybrid architectures. Current GPUs offer not only an ample parallelism, but also remarkable flops-per-Watt ratios and competitive economical cost. This has motivated the development of boards that embed one or more general-purpose low-power processors (like those developed for mobile devices by ARM) with low-power GPUs. The performance and moderate power consumption of such hybrid boards has motivated the assembly of powerful clusters with hundreds of these boards. This is the case of the Tibidabo supercomputer at the Barcelona Supercomputer Center [22].
The GH algorithm combines highly parallel operations suitable for GPUs and fine-grain parallelism computations (mainly due to pivoting) that suits general-purpose processors. Thus, this algorithm represents a good candidate for hybrid CPU-GPU platforms.
In this context, we present two implementations of the GH algorithm that target hybrid CPU-GPU low-power platforms. The first variant performs all computations in the GPU. The second variant distributes the computations between the CPU and the GPU, but incurs in a overhead due to data transfers between the CPU and the GPU memories.
3.1 GPU version (GH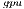 )
)
Due to the moderate computational power offered by the general-purpose processor when compared with that offered by the GPU, this implementation performs all the computations in the latter. On the other hand, the main drawback of GH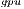 is that not all the computational units in the platform are employed. This variant is an implementation of algorithm gausshuard_blk using the kernels offered by the CUBLAS library, i.e., the implementation of the BLAS provided by NVIDIA.
is that not all the computational units in the platform are employed. This variant is an implementation of algorithm gausshuard_blk using the kernels offered by the CUBLAS library, i.e., the implementation of the BLAS provided by NVIDIA.
In an initial phase, the whole 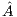 matrix is transferred from the CPU to the GPU. Then, the algorithm proceeds in the GPU, and upon completion, the last column of
matrix is transferred from the CPU to the GPU. Then, the algorithm proceeds in the GPU, and upon completion, the last column of 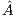 , containing
, containing 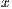 , is transferred back to the CPU memory.
, is transferred back to the CPU memory.
As previously stated, most of the computational effort in algorithm gausshuard_blk lies in the matrix-matrix products. To fully exploit the capabilities of the GPU during the execution of these products, the matrices involved must be of a moderate to large size. The dimension of these matrices is determined by the system dimension, 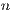 , and the algorithmic block size,
, and the algorithmic block size, 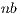 . Consequently, a small value of
. Consequently, a small value of 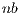 limits the performance of this variant. On the other hand, a large value of
limits the performance of this variant. On the other hand, a large value of 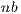 increases the relative computational effort of the block diagonalization, which is a BLAS-2 operation that delivers limited performance. To partially overcome this problem, we included a multiple nested algorithmic block sizes strategy in GH
increases the relative computational effort of the block diagonalization, which is a BLAS-2 operation that delivers limited performance. To partially overcome this problem, we included a multiple nested algorithmic block sizes strategy in GH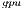 . Specifically, the block diagonalization is performed via a blocked variant of the GH algorithm, i.e.,
. Specifically, the block diagonalization is performed via a blocked variant of the GH algorithm, i.e., 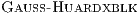 . As a result, BLAS-3 kernels can be employed during most of this computation. To maximize the performance of GH
. As a result, BLAS-3 kernels can be employed during most of this computation. To maximize the performance of GH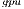 , both algorithmic block-sizes must be carefully chosen.
, both algorithmic block-sizes must be carefully chosen.
3.2 Hybrid Version(GH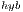 )
)
This variant aims to exploit both available computational resources in the platform, i.e., the CPU and GPU. To achieve this, it requires data transfers between the CPU and the GPU and, consequently, incurs a certain overhead due to communications. To alleviate this, as an initial phase, the matrix 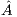 is transferred from the CPU memory to the GPU memory. With this we avoid to transfer the panel
is transferred from the CPU memory to the GPU memory. With this we avoid to transfer the panel ![[ ˆA11,A ˆ12]](/img/revistas/cleiej/v19n1/1a0298x.png) from CPU to GPU at each iteration of the algorithm. The total amount of data transferred remains the same but, given the platform specifications, a single larger data transfer is more efficient than several smaller transfers. Furthermore, this data transfer can be partly overlapped with the diagonalization of the first panel. This way, we save time as well as energy.
from CPU to GPU at each iteration of the algorithm. The total amount of data transferred remains the same but, given the platform specifications, a single larger data transfer is more efficient than several smaller transfers. Furthermore, this data transfer can be partly overlapped with the diagonalization of the first panel. This way, we save time as well as energy.
Most of the computations in the algorithm are cast in terms of matrix-matrix products. This operation exhibits a high level of concurrency and suits the GPU architecture. In contrast, the block diagonalization presents a moderate cost and its concurrency is constrained by the pivoting scheme. Thus, the natural way to distribute the operations is to perform the matrix-matrix products in the GPU and the block diagonalization in the CPU. Therefore, the bulk of the computations are performed in the most powerful processor, the GPU. This partitioning of the workload (diagonalization in the CPU and the remaining block eliminations in the GPU) requires that, at each step of the gausshuard_blk algorithm, the block ![[ ˆA11,Aˆ12]](/img/revistas/cleiej/v19n1/1a0299x.png) is sent from the GPU (after completing the block-row elimination) to the CPU and retrieved from there back into the GPU (after the computation of the block diagonalization). Consequently, the volume of data transferred at each iteration of the algorithm is proportional to
is sent from the GPU (after completing the block-row elimination) to the CPU and retrieved from there back into the GPU (after the computation of the block diagonalization). Consequently, the volume of data transferred at each iteration of the algorithm is proportional to 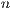 and
and 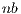 . After the procedure is completed, the solution vector (stored in the last column of
. After the procedure is completed, the solution vector (stored in the last column of 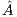 ) must be sent to the CPU.
) must be sent to the CPU.
Similarly to the fully GPU implementation, GH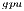 , the efficiency of GH
, the efficiency of GH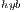 strongly depends on the value of
strongly depends on the value of 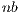 : small values of
: small values of 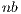 close to
close to 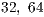 , limit the performance of the matrix-matrix products performed in the GPU, though this ensures that the execution of the algorithm is driven by computation instead of data transfers. However, a large value of
, limit the performance of the matrix-matrix products performed in the GPU, though this ensures that the execution of the algorithm is driven by computation instead of data transfers. However, a large value of 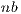 may hurt the performance of GH
may hurt the performance of GH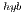 because a significant part of the computations is mapped to the less powerful processor, the CPU. Again, we propose to perform the block diagonalization via a blocked variant of the algorithm and, therefore, we leverage a double algorithmic block size, namely
because a significant part of the computations is mapped to the less powerful processor, the CPU. Again, we propose to perform the block diagonalization via a blocked variant of the algorithm and, therefore, we leverage a double algorithmic block size, namely 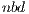 and
and 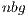 . The former is uniquely employed for the computations in the ARM processor, i.e., during the block diagonalization. This way, BLAS-3 kernels can be employed during this stage, accelerating its execution. At a higher level, in gausshuard_blk we set
. The former is uniquely employed for the computations in the ARM processor, i.e., during the block diagonalization. This way, BLAS-3 kernels can be employed during this stage, accelerating its execution. At a higher level, in gausshuard_blk we set 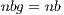 . A more efficient execution of the block diagonalization phase permits to chose larger values for
. A more efficient execution of the block diagonalization phase permits to chose larger values for 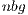 , which also yield higher performance during the execution of the matrix-matrix products in the GPU. Additionally, larger values of
, which also yield higher performance during the execution of the matrix-matrix products in the GPU. Additionally, larger values of 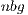 reduce the number of iterations and, thus, the number of data transfers (despite it might increase the amount of data transferred, transfers will be performed in a more efficient manner).
reduce the number of iterations and, thus, the number of data transfers (despite it might increase the amount of data transferred, transfers will be performed in a more efficient manner).
Additionally, GH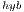 makes a heavy use of tuned computational kernels in OpenBLAS and NVIDIA CUBLAS, respectively, for the ARM and the GPU processors. Moreover, a few key scalar and Level-1 BLAS operations are performed via ad-hoc kernels, parallelized with OpenMP, which yield higher performance than their counterparts in OpenBLAS.
makes a heavy use of tuned computational kernels in OpenBLAS and NVIDIA CUBLAS, respectively, for the ARM and the GPU processors. Moreover, a few key scalar and Level-1 BLAS operations are performed via ad-hoc kernels, parallelized with OpenMP, which yield higher performance than their counterparts in OpenBLAS.
4 Experimental evaluation
In this section we show the experimental evaluation of the GH-based solvers introduced in the previous section. The evaluation focuses on two aspects, performance (measured in execution time and GFLOPS) and energy consumption. All experiments are performed employing single precision arithmetic. We compare the solvers on the solution of randomly generated systems of dimension 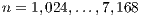 .
.
The novel codes has been tuned for the hardware platform employed, and compared with two LU-based solvers considered as the state-of-the-art for ARM processors and hybrid CPU-GPU platforms. In particular, the solver in OpenBLAS v.0.2.14 to exploit the ARM processor and its counterpart in MAGMA v.1.6.2 to leverage the CPU and GPU processors. Note that the routine in MAGMA internally uses kernels in OpenBLAS to perform computations in the ARM.
4.1 Experimental platform
The experimental hardware platform, a JETSON TK1 [23] board, is composed of a Tegra K1 SoC (Systems on a Chip) processor with 2GB of DDR3L RAM. In more detail, the Tegra K1 includes an NVIDIA GPU with 192 CUDA Kepler cores and an ARM quad-core Cortex-A15 processor at 2.32 GHz.
The board runs an extended version of Linux Ubuntu 14.04 adapted for the ARM architecture. The codes for the ARM are compiled using gcc v.4.8.2, while the codes developed for the NVIDIA GPU are compiled with nvcc v.6.0.1.
The platform configuration was adapted such that the maximum performance level was reported with a negligible loss of energy efficiency. This involved to: (1) set the frequency governor of the CPU to performance (instead of its default value, ondemand), (2) turn on the ARM-cores as required, (3) and set the GPU clock to the highest available frequency, i.e., 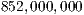 Hz (by default set to
Hz (by default set to 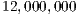 Hz).
Hz).
4.2 Performance evaluation
The runtimes showed for the different GPU-variants include the overhead associated with data transfers between CPU and GPU memory spaces.
The quality of the numerical results obtained with all solvers are numerically equivalent. In other words, the residual error associated with all the computed solutions are of the same order.
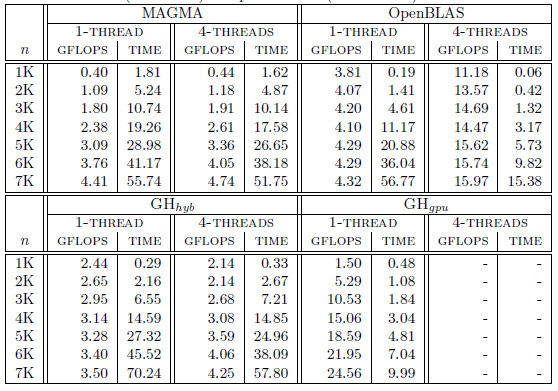
Table 1 summarizes the runtime (in seconds) and performance (in GFLOPS or billions of flops per second) obtained by the four solvers, i.e., OpenBLAS, MAGMA, GH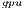 and GH
and GH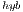 . Additionally, for each variant (except GH
. Additionally, for each variant (except GH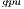 ), we include the number of threads employed on the CPU. In particular, we present two options for each variant, corresponding to the use a single thread and use 4 threads (one per core in the Cortex A-15 processor). For GH
), we include the number of threads employed on the CPU. In particular, we present two options for each variant, corresponding to the use a single thread and use 4 threads (one per core in the Cortex A-15 processor). For GH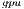 and GH
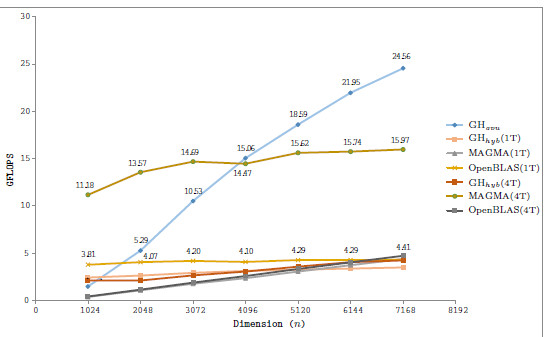
and GH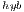 , we evaluate several block sizes (both, internal and external), but for simplicity, only the best performance for each system dimension is shown. A graphical comparison of the performance attained by all variants is offered in Figure 6.
, we evaluate several block sizes (both, internal and external), but for simplicity, only the best performance for each system dimension is shown. A graphical comparison of the performance attained by all variants is offered in Figure 6.
First of all, we focus on the results obtained with solvers in OpenBLAS and MAGMA. The solver in the MAGMA library reports a moderate performance on the solution of small to moderate-scale systems. This might be caused by the CPU-GPU communication overhead. The performance rapidly improves with the problem dimension. Additionally, the use of 4 threads (note that MAGMA offers a hybrid CPU-GPU method) delivers marginal gains, about a 10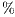 of time reduction. OpenBLAS offers a remarkable performance despite it uses only the ARM processor (that presents a lower computational power than the GPU), but its performance is far from that of GPU-based solvers. ts parallel version is able to beat the MAGMA solver for all problem dimensions.
of time reduction. OpenBLAS offers a remarkable performance despite it uses only the ARM processor (that presents a lower computational power than the GPU), but its performance is far from that of GPU-based solvers. ts parallel version is able to beat the MAGMA solver for all problem dimensions.
Regarding the GH-based solvers, the hybrid variant (GH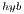 ) offers execution times comparable with those obtained with the MAGMA library for the larger problems, but it is clearly superior on the solution of small systems, especially when a single thread is employed in the CPU. In contrast, the GH
) offers execution times comparable with those obtained with the MAGMA library for the larger problems, but it is clearly superior on the solution of small systems, especially when a single thread is employed in the CPU. In contrast, the GH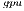 variant, which performs all the computations in the GPU, achieves a remarkable performance, especially for larger problems. This is because the capabilities of the massively parallel architecture in the GPU can be exploited more efficiently in the solution of large systems. It should be note that GH
variant, which performs all the computations in the GPU, achieves a remarkable performance, especially for larger problems. This is because the capabilities of the massively parallel architecture in the GPU can be exploited more efficiently in the solution of large systems. It should be note that GH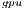 is the best option for problems of dimension
is the best option for problems of dimension 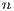 larger than
larger than 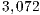 .
.
In a conclusion, the hybrid implementations do not attain high performance because of the high overhead introduced by the data transfers. For the solution of small problems, the use of the ARM processor only is convenient since it does not require of data transfer. For larger problems, the higher computational power of the GPU promotes the GPU-only variant as the best option.
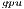 solvers.
solvers.
4.3 Power consumption evaluation
In this section we address the power and energy evaluation of the two more efficient solvers, i.e., the solver in the OpenBLAS library and GH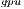 . We exclude from this comparison the hybrid solvers (GH
. We exclude from this comparison the hybrid solvers (GH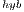 and the solver in the MAGMA library) because the power required by them is expected to be higher than that of the solvers that are fully executed in one of the processors in the platform. Additionally, they exhibited a higher runtime and thus, larger energy requirements are to be expected by the hybrid solvers. For the OpenBLAS solver we evaluate its behavior with 1 and 4 threads.
and the solver in the MAGMA library) because the power required by them is expected to be higher than that of the solvers that are fully executed in one of the processors in the platform. Additionally, they exhibited a higher runtime and thus, larger energy requirements are to be expected by the hybrid solvers. For the OpenBLAS solver we evaluate its behavior with 1 and 4 threads.
In order to measure the power consumption, we connected a WattsUp?Pro wattmeter (accuracy of 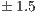 % and a rate of 1 sample/sec.) to the power line from the electric socket to the power supply unit (PSU) of the Tegra TK1 device. Thus we measure the power consumption of the whole board. The power measurements are collected, stored, and treated in a different server, so that the measurement does not disturb the solvers execution. All tests were executed for a minimum of 1 minute, after a warm-up period of 2 minutes.
% and a rate of 1 sample/sec.) to the power line from the electric socket to the power supply unit (PSU) of the Tegra TK1 device. Thus we measure the power consumption of the whole board. The power measurements are collected, stored, and treated in a different server, so that the measurement does not disturb the solvers execution. All tests were executed for a minimum of 1 minute, after a warm-up period of 2 minutes.
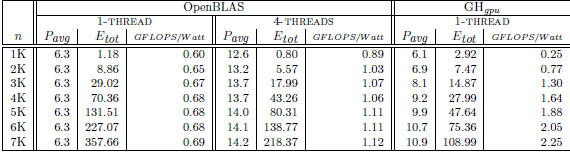
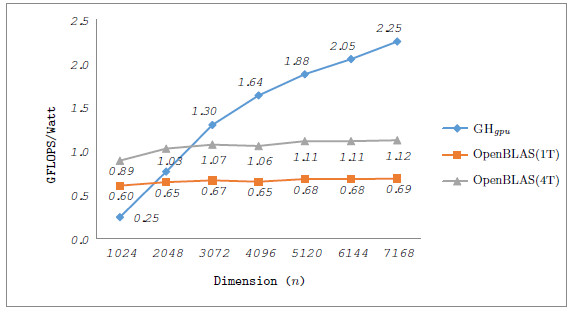
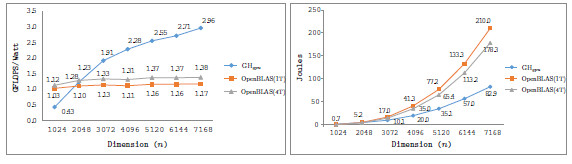
Table 2 collects the average power (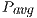 ), total energy (
), total energy (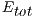 ), and GFLOPS/Watt reported by the solvers. Figure 7 shows the GFLOPS/Watt ratio of the solvers. The results show that, when the system dimension
), and GFLOPS/Watt reported by the solvers. Figure 7 shows the GFLOPS/Watt ratio of the solvers. The results show that, when the system dimension 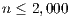 , the most energy-efficient solver is that provided by the OpenBLAS library (using 4 threads). This is explained by the absence of expensive CPU-GPU data transfers. Although the GPU architecture is more energy-efficient than the ARM processors, it cannot be fully exploited for the solution of small problems. Thus, the time and energy spent in data transfers is superior to the gains reported by the GPU usage. This is exposed by the
, the most energy-efficient solver is that provided by the OpenBLAS library (using 4 threads). This is explained by the absence of expensive CPU-GPU data transfers. Although the GPU architecture is more energy-efficient than the ARM processors, it cannot be fully exploited for the solution of small problems. Thus, the time and energy spent in data transfers is superior to the gains reported by the GPU usage. This is exposed by the 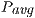 values. GH
values. GH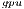 delivers a lower
delivers a lower 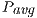 but a longer execution time (see Table 4.2), resulting in higher energy consumption. For larger systems, the GH
but a longer execution time (see Table 4.2), resulting in higher energy consumption. For larger systems, the GH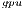 reported the best results in terms of energy. For this kind of problems, the full exploitation of the GPU capabilities compensates the time and energy spent in data transfers (note than only two data transfers are required in GH
reported the best results in terms of energy. For this kind of problems, the full exploitation of the GPU capabilities compensates the time and energy spent in data transfers (note than only two data transfers are required in GH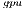 , initially the whole
, initially the whole 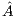 matrix is sent to the GPU and, upon completion, the
matrix is sent to the GPU and, upon completion, the 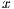 vector is retrieved by the CPU). A special case occurs when
vector is retrieved by the CPU). A special case occurs when 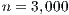 . In this case, the solver in OpenBLAS (with 4 threads) reports the shorter execution time, but due to the lower
. In this case, the solver in OpenBLAS (with 4 threads) reports the shorter execution time, but due to the lower 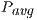 of GH
of GH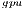 , the latter consumes less energy. If we focus on the
, the latter consumes less energy. If we focus on the 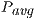 results, the OpenBLAS solver with a single thread presents the lowest power consumption. This is explained by the fact that the solver uses a single core of the ARM processor. On the other hand, when the same solver operates with 4 threads, it delivers a speed-up of about 3.5, while the power is nearly doubled. Consequently, the use of 4 threads in OpenBLAS is more energy-efficient. The average power consumed by GH
results, the OpenBLAS solver with a single thread presents the lowest power consumption. This is explained by the fact that the solver uses a single core of the ARM processor. On the other hand, when the same solver operates with 4 threads, it delivers a speed-up of about 3.5, while the power is nearly doubled. Consequently, the use of 4 threads in OpenBLAS is more energy-efficient. The average power consumed by GH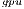 (remember this solver is completely executed in the GPU) is lower than that of the parallel OpenBLAS kernel (using 4 cores of the ARM processor), reporting up to 50% of power reduction depending on the system dimension. This implies that the GPU presents a higher peak performance and also a lower energy-consumption and thus, this architecture specially appealing for our purposes.
(remember this solver is completely executed in the GPU) is lower than that of the parallel OpenBLAS kernel (using 4 cores of the ARM processor), reporting up to 50% of power reduction depending on the system dimension. This implies that the GPU presents a higher peak performance and also a lower energy-consumption and thus, this architecture specially appealing for our purposes.
 .
. 
 solvers.
solvers.
Since the platform contains several devices —e.g., network interface cards— we measured the average power while idle for 1 minute,  , showing a value of 2.6 Watts. This correspond to the power consumption of the board when no operation is executed. We use this value to compute the net energy, corresponding to the energy consumption that is obtained after subtracting
, showing a value of 2.6 Watts. This correspond to the power consumption of the board when no operation is executed. We use this value to compute the net energy, corresponding to the energy consumption that is obtained after subtracting 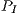 from the power samples. The net energy approximates the actual energy spent in computations, and allows a fair comparison between the computational kernels. Figure 8 shows the GFLOPS/Watt computed with the average net power (left) and the net energy of the solvers. Both figures show the superiority of GH
from the power samples. The net energy approximates the actual energy spent in computations, and allows a fair comparison between the computational kernels. Figure 8 shows the GFLOPS/Watt computed with the average net power (left) and the net energy of the solvers. Both figures show the superiority of GH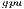 , because it performs more arithmetic operations per Watt and also requires less energy.
, because it performs more arithmetic operations per Watt and also requires less energy.
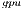 solvers.
solvers.
5 Concluding Remarks
During the last years, energy consumption has become a major issue in high performance computing, too. In this work we present two efficient solvers for linear sytems of equations that present remarkably low energy consumption. The new solvers exploit the capabilities of a low-power hardware platform, an NVIDIA JETSON K1 (formed by an ARM quad-core processor and a NVIDIA GPU with 192 CUDA cores) device to efficiently run a Gauss-Huard-based solver. The Gauss-Huard algorithm presents some features which turn it more suitable for the target hardware platform than the traditional LU-based solver. The GH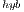 solver aims to exploit all the computational units in the platform concurrently. Despite it is able to perform computations concurrently in both processors, it also requires data transfers between their memory spaces, incurring into a considerable overhead. The GH
solver aims to exploit all the computational units in the platform concurrently. Despite it is able to perform computations concurrently in both processors, it also requires data transfers between their memory spaces, incurring into a considerable overhead. The GH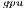 solver performs all the computations in the most powerful processor, the GPU. Thus, it incurs a minor communication overhead that is compensated with both higher performance and energy-efficiency of the GPU. The performance of both solvers is compared with the solvers in OpenBLAS and MAGMA libraries. The experimental results show the superior behavior of the GH
solver performs all the computations in the most powerful processor, the GPU. Thus, it incurs a minor communication overhead that is compensated with both higher performance and energy-efficiency of the GPU. The performance of both solvers is compared with the solvers in OpenBLAS and MAGMA libraries. The experimental results show the superior behavior of the GH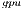 solver on the solution of linear systems of dimension
solver on the solution of linear systems of dimension 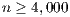 . For smaller systems, the OpenBLAS solver reports the best execution times because it runs entirely in the ARM processor and does not require any CPU-GPU communication. The power and energy evaluation show the convenience of the GPU processor over the ARM quad-core. The GPU consumes less power and delivers a higher GFLOPS rate. Consequently, the GH
. For smaller systems, the OpenBLAS solver reports the best execution times because it runs entirely in the ARM processor and does not require any CPU-GPU communication. The power and energy evaluation show the convenience of the GPU processor over the ARM quad-core. The GPU consumes less power and delivers a higher GFLOPS rate. Consequently, the GH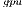 variant attains the best energy-efficiency on the solution of moderate to large-scale systems. On the solution of small systems, again the absence of CPU-GPU communications in the OpenBLAS kernel turns it into the most energy-efficient variant. The communication overhead affects negatively the performance (and therefore the energy efficiency) of the hybrid solvers (i.e., the solver in the MAGMA library and GH
variant attains the best energy-efficiency on the solution of moderate to large-scale systems. On the solution of small systems, again the absence of CPU-GPU communications in the OpenBLAS kernel turns it into the most energy-efficient variant. The communication overhead affects negatively the performance (and therefore the energy efficiency) of the hybrid solvers (i.e., the solver in the MAGMA library and GH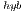 ) and thus, both deliver limited performance.
) and thus, both deliver limited performance.
There are different aspects that were not addressed in the current work but deserve more investigation. For example, it is important to study new techniques to improve the results of the hybrid solvers. For example techniques like look-ahead [24] have demonstrated important benefits in similar applications. It should also be evaluated how the hybrid CPU-GPU implementations can benefit from the improvements in the Unified-Memory-Access announced by NVIDIA for their future devices. Additionally, we plan to extend this study to other low power consumption hardware platforms, e.g., Samsung ODROID-XU4. Finally, although this work targets single precision arithmetic (due to the low performance of the architecture on double precision), we plan to investigate how GH can be complemented with an iterative refinement to attain a full double precision solution.
Acknowledgment
Juan Silva, Ernesto Dufrechou and Pablo Ezzatti acknowledge the support from Programa de Desarrollo de las Ciencias Básicas, and Agencia Nacional de Investigación e Innovación, Uruguay. Enrique S. Quintana-Ortí was supported by project TIN-2014-53495-R of the Ministerio de Economía y Competitividad and FEDER. All researchers acknowledge the support from the EHFARS project funded by the German Ministry of Education and Research BMBF.
References
[1] J. W. Demmel, Applied Numerical Linear Algebra. Philadelphia, PA, USA: Society for Industrial and Applied Mathematics, 1997.
[2] G. Golub and C. V. Loan, Matrix Computations, 3rd ed. Baltimore: The Johns Hopkins University Press, 1996.
[3] J. J. Dongarra, J. D. Croz, S. Hammarling, and I. Duff, “A set of level 3 basic linear algebra subprograms,” ACM Trans. Math. Soft., vol. 16, no. 1, pp. 1–17, March 1990.
[4] P. Ezzatti, E. Quintana-Ortí, and A. Remón, “Using graphics processors to accelerate the computation of the matrix inverse,” The Journal of Supercomputing, vol. 58, pp. 429–437, 2011. [Online]. Available: http://dx.doi.org/10.1007/s11227-011-0606-4
[5] P. Benner, P. Ezzatti, E. S. Quintana-Ortí, and A. Remón, “Matrix inversion on CPU-GPU platforms with applications in control theory,” Concurrency and Computation: Practice and Experience, vol. 25, no. 8, pp. 1170–1182, 2013. [Online]. Available: http://dx.doi.org/10.1002/cpe.2933
[6] P. Huard, “La méthode simplex sans inverse explicite,” EDB Bull, Direction Études Rech. Sér. C Math. Inform. 2, pp. 79–98, 1979.
[7] T. J. Dekker, W. Hoffmann, and K. Potma, “Stability of the Gauss-Huard algorithm with partial pivoting,” Computing, vol. 58, pp. 225–244, 1997.
[8] J. P. Silva, E. Dufrechou, E. Quintana-Ortí, A. Remón, and P. Benner, “Solving dense linear systems with hybrid CPU-GPU platforms,” in Proceedings of the XLI Latin American Computing Conference, CLEI 2015, Arequipa, Peru, 2015. IEEE, to appear.
[9] OpenBLAS website, Z. Xianyi; [accessed 2015 Dec], http://www.openblas.net/.
[10] B. J. Smith, “R package MAGMA: Matrix algebra on GPU and multicore architectures, version 0.2.2,” September 3, 2010, [On-line] http://cran.r-project.org/package=magma.
[11] J. A. Gunnels, F. G. Gustavson, G. M. Henry, and R. A. van de Geijn, “FLAME: Formal linear algebra methods environment,” ACM Trans. Math. Soft., vol. 27, no. 4, pp. 422–455, 2001.
[12] P. Bientinesi, J. A. Gunnels, M. E. Myers, E. S. Quintana-Ortí, and R. A. van de Geijn, “The science of deriving dense linear algebra algorithms,” ACM Trans. Math. Soft., vol. 31, no. 1, pp. 1–26, 2005.
[13] E. Anderson, Z. Bai, J. Demmel, J. E. Dongarra, J. DuCroz, A. Greenbaum, S. Hammarling, A. E. McKenney, S. Ostrouchov, and D. Sorensen, LAPACK Users’ Guide. Philadelphia: SIAM, 1992.
[14] N. J. Higham, Accuracy and Stability of Numerical Algorithms, 2nd ed. Philadelphia, PA, USA: Society for Industrial and Applied Mathematics, 2002.
[15] E. Quintana-Ortí, G. Quintana-Ortí, X. Sun, and R. van de Geijn, “A note on parallel matrix inversion,” SIAM J. Sci. Comput., vol. 22, pp. 1762–1771, 2001.
[16] T. J. Dekker, W. Hoffmann, and K. Potma, “Parallel algorithms for solving large linear systems,” Journal of Computational and Applied Mathematics, vol. 50, no. 1–3, pp. 221–232, 1994.
[17] W. Hoffmann, K. Potma, and G. Pronk, “Solving dense linear systems by Gauss-Huard’s method on a distributed memory system,” Future Generation Computer Systems, vol. 10, no. 2–3, pp. 321–325, 1994.
[18] TOP500.org; [accessed 2015 Dec], http://www.top500.org/.
[19] MAGMA, Univ. of Tennessee; [accessed 2015 Dec], http://icl.cs.utk.edu/magma/.
[20] S. Balay, W. Gropp, L. C. McInnes, and B. Smith, “PETSc 2.0 users manual,” Argonne National Laboratory, Tech. Rep. ANL-95/11, October 1996.
[21] TU Wien and FASTMathSciDAC Institute, http://viennacl.sourceforge.net/.
[22] Barcelona Supercomputing Center, http://www.bsc.es.
[23] NVIDIA, http://www.nvidia.com/object/jetson-tk1-embedded-dev-kit.html.
[24] P. Strazdins, “A comparison of lookahead and algorithmic blocking techniques for parallel matrix factorization,” Department of Computer Science, The Australian National University, Canberra 0200 ACT, Australia, Tech. Rep. TR-CS-98-07, 1998.