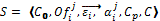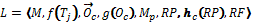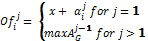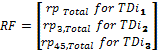Servicios Personalizados
Revista
Articulo
Links relacionados
Compartir
CLEI Electronic Journal
versión On-line ISSN 0717-5000
CLEIej vol.16 no.2 Montevideo ago. 2013
Mathematical Models of Coordination Mechanisms in Multi-Agent Systems
Juan Terán
Universidad de Los Andes, CEMISID
Mérida, Venezuela, 5101
José L. Aguilar
Universidad de Los Andes, CEMISID
Mérida, Venezuela, 5101
and
Mariela Cerrada
Universidad de Los Andes, CEMISID
Mérida, Venezuela, 5101
Abstract
The good performance of a set of computer systems based on agents depends on the coherence degree and coordination between their activities. The study of coordination problem is an important topic for designers and researchers in the multi-agents systems field. There are several coordination mechanisms in the current literature, being the auction and the contract net the most popular ones. These mechanisms allow the agents to allocate resources and tasks to achieve their objectives. This paper aims to present formal models of the auction and the contract net as coordination mechanisms in multi-agents systems based on FIPA (Foundation for Intelligent Physical Agents) Protocols. Mathematical equations describe the different parameters characterizing the auction and the contract net mechanisms; they allow define a generic structure of each mechanism and groups of agents can create several instances of them to coordinate their needs.
Spanish abstract
El buen desempeño de un conjunto de sistemas computacionales basados en agentes depende del grado de coherencia y la coordinación entre sus actividades. El estudio de la coordinación es un tópico importante entre diseñadores e investigadores en el área de sistemas multi-agentes. Existen diversos mecanismos de coordinación en la literatura actual, siendo la subasta y la red de contratos los más populares. Estos mecanismos permiten asignar recursos y tareas a los agentes para el logro de sus objetivos. Este trabajo tiene como finalidad presentar modelos formales para la subasta y la red de contratos como mecanismo de coordinación en sistema multi-agentes basados en protocolos FIPA (Fundación para Agentes Físicos Inteligentes, por sus siglas en inglés). Las ecuaciones matemáticas describen los diferentes aspectos que caracterizan los mecanismos de subasta y red de contratos; permitiendo la definición de una estructura genérica para cada mecanismo y grupos de agentes pueden crear varias instancias de ellos para coordinar sus necesidades.
Keywords: Agents, Coordination mechanisms, Auction protocol, Contract net protocol.
Spanish keywords: Agentes, Mecanismo de coordinación, protocolo de Subasta, Protocolo Contract net
Received 2012-05-30, Revised 2013-01-15, Accepted 2013-01-15
1 Introduction
Coordination is a central issue in agents-based software, and specifically in distributed artificial intelligence (1). The coordination can be addressed from two major point of view, cooperation and negotiation. Cooperation is a kind of coordination that consist in many agents with non-antagonist interactions (an agent's actions do not harm the others) in order to achieve common goals. The negotiation can achieve accords in the agents of a system, when each one defends its own interests, leading to a situation that benefits all (2). Particularly, the negotiation is essential to reach the agreements among agents. In this case, there are not common goals between the agents, for this reason it is necessary the negotiation mechanisms to achieve their goals. The auction and the contract net (also called tender) are common negotiation protocols. In the following, we present some recent works that use auction protocol in multi-agents systems. In (3) it is presented a framework for the design and analysis of coordination mechanisms based on auctions for cooperation among agents. The real-time distributed task allocation in robots based on an auction algorithm is studied in (4), this approach is called sequential auction incremental values (SIV). The idea behind SIV auctions is to assign as many tasks per round to robots as possible as long as their individual costs for performing these tasks are under a given bound, which increases exponentially from round to round. The work (5) proposes an approach to improve the performance of agents using auction mechanisms in real time based on the idea of task assignment; here an agent can receive a great penalty when a task is not assigned to him. On the other hand, in (6) it is developed a mechanism based on market and trade strategies for intelligent networks, specifically using continuous double auction. With respect to the contract net, a standards-based three-dimensional taxonomy of contract net are defined in (7) following three criteria: the hierarchy, the type and flexibility to be used for optimizing the selection of the winning candidate. In (8) it is presented an application of a multi-agent system using a contract net protocol for the distribution of energy resources by using a MicroGrid, which is a distributed network of low voltage generators. Finally, an automated system of design and analysis of tasks allocation in multi-agent systems it is presented in (9). They propose a combination of the Vickrey auction and contract net protocols. The advantage of this approach is that it is applicable in a wide range of realistic scenarios, where complex knowledge of negotiations among agents are not feasible, and the future changes in the environment are unforeseen, which can require that the agents violate their contracts.
In general, none of the previous works propose a formal model of the protocols of auction or tender (variables, actors, restrictions, etc.), this is the main contribution of this paper. This models allows us to characterize the different types of auction (English, Dutch, One Shut), and the contract net mechanisms. The aim of this paper is to present generic models that describe both mechanisms under FIPA standards (10), (11). The implicit variables, the roles and constraints present in each protocol are defined, among other. This formalization allows us to manipulate the agents using cultural algorithms in the context of an optimization model that determines the optimal coordination scheme for a given multi-agent system. The paper is organized as follows: Section 2 discusses the main theoretical aspects on auction and contract net mechanisms. Section 3 presents the proposed formal models for both auction and contract net. Section 4 presents a case study with an example for each mechanism. Finally, the conclusions are given.
2 Auction and Contract Net Protocols in Multi-Agent Systems
In this section, we present the theoretical bases of the coordination mechanisms studied in this work.
2.1 Auction Protocols
The auction mechanisms have been used in many practical applications of computer science that involve the allocation of goods, tasks and resources. One reason about why the auction has become so popular is that it is an extremely simple interaction scenario, and therefore easy to automate. An auction mechanism is made up by a group of agents, where one agent has the role of auctioneer and the remaining agents are bidders (12). The classic scenario assumes that the auctioneer wants to sell an item at the highest price possible, while the bidders want to buy at the lowest price possible. Let's consider some of the dimensions along which auction protocols may vary (12):
i. The winner assignment: this process defines who gets the good that the bidders are bidding for. The good is allocated to the agent with the best bid. Such protocols are known as first-price auctions. A second way it is to allocate the good to the agent that have the highest bid, but this agent pays only the amount of the second highest bid. Such auctions are known as second-price auctions.
ii. Tenders visibility: the second dimension which the auction protocols can vary is whether the bids of the agents are known to each other or not. If every agent can see what every other agent is bidding (the bids are common knowledge), then the auction is said to be open bid. If the agents are not able to determine the bids made by other agents, then the auction is said to be a sealed-bid auction.
iii. Tenders submission: a third dimension is the mechanism by which the bidding proceeds. The simplest way is to have a single round of bidding, after which the auctioneer allocates the good to the winner. Such auctions are known as one shot. The second possibility is the price starts low (often a reservation price) and successive bids are for increasingly large amounts. Such auctions are known as ascending. The alternative - descending - is when the auctioneer starts with a high value to decrease the price in successive rounds. The value of the auctioned item (valuation) is:
· Private value: the value of the item depends only on the agent's own preferences. The winning bidder will not resell or make good display against the other (otherwise the value would depend on the valuations of other agents). An example is the auction of a cake the winner will eat.
· Common value: the value that an agent gives to an item depends entirely on the value that other agents have of. For example, the value of treasury bonds depends entirely on its potential for resale.
· Correlated value: The value assigned by an agent depends partly on their own preferences and partly on the valuations of other agents. For example, an agent buys a painting (or car) that maybe re-sells in the future.
Different auction protocols can be obtained by varying the dimensions above, next section present some examples.
2.1.1 English Auction:
It is the most popular auction mechanism (12). It is first-price, open bid, and ascending. The main characteristics are:
· The auctioneer starts the auction with a price for the initial resource (which may be zero); if there are not agents offering more than the initial price, then the resource is assigned to the auctioneer.
· Offers are made by the bidders agents, who must offer more than the previous offer. Agents can see all the offers made, and are able to participate in the bidding process when they consider.
· When there are not agents that like to improve the current offer (the highest), the auction is over and the agent must pay the ultimate price offered. Figure 1 a) shows this auction protocol proposed by FIPA.
2.1.2 Dutch Auction: the main characteristics are:
· This is an example of open bid and descending auction (12):
· The auctioneer starts offering a starting price slightly above its expected value.
· The auctioneer starts to lower the price continuously, until an agent offers this price, which will be the final price to pay for that agent.
2.1.3 First-price and a sealed-Bid auctions: the characteristics are:
· They are examples of a single round auction (One Shut), and are perhaps the simplest of all auction types.
· They execute a single round, in which bidders send their bids to the auctioneer, without making them public to other agents, (i. e., they are private).
· There are not subsequent rounds and it is assigned to the agent that offers the most value.
There are other protocols as Vickrey, Double auction, etc. In this paper we treat the English protocol.
2.2 The Contract Net Protocol
The Contract net, designed by Randall Davis and Reid Smith (13), are mechanisms used for collaborative problems solving. In this case, the goal is that several agents communicate and coordinate with each other, so they can carry out a task whose complexity makes it difficult to be performed by a single agent. Each agent in the network takes one or two roles related to the execution of an individual task: manager or contractor (14). When an agent has the manager role must carry out certain activities, which are: (i) break a complex task into less complex subtasks, and so it will be easier to solve, (ii) announce to other agents that there is a sub-task expecting to be executed. These ads are distributed through a broadcast message to all agents or are directed to a specific group of agents, (iii) when it receives the response to their requests, the manager selects the most appropriate offer and assign this sub-task to this agent, for which a contract is created, (iv) monitor the progress of the contract, possibly asking for information, reports, etc. It is free to reassign the subtask if the contractor fails to complete, finally, (v) integrate the partial results produced by the contractors in a complete solution. Meanwhile, the contractors agents perform the following activities: (i) receive announcements of tasks and assess their skills and availability to perform them, (ii) if they are able to satisfactorily perform the task, make an offer, and (iii) if this offer is accepted they reserve the resources required for its execution. When the contractors have won bids, they must perform the tasks assigned to them, and generate reports about the progress of these tasks and their final results. The contractor agents can become managers if the subtask is too complex for their abilities, then they subdivide the sub-task and the process of assignation of task is repeated. In summary, the protocol uses a number of basic messages (15):
· Notification of the task - sent by the manager agent to announce the availability of a task and the need for contractors
· Offer - sent by the contractor agents when they are available to perform a task
· Winner - sent by the manager agent to the contractor, stating that he is now responsible for the task
· Report - submitted by the contractor agent to the administrator/manager agent stating whether or not successfully it executes the task and the results (also, it sends partial results).
These messages provide the functionality needed to make the contracts between agents (15). The FIPA interaction diagram of this protocol is shown below in Figure 1b) (11).
3 Auction and the Contract Net Mathematical Models
This section defines the different variables, roles and constraints describing the coordination mechanisms that are studied in this paper: auction and contract net.
3.1 Formal Model of Auction Mechanism
Suppose a group of agents A = (as, Ai), where as is the auctioneer agent and Ai is the set of bidders agents defined by Ai ={ A1 , A2 , A3 ,
, An }, an auction is defined by the tuple S (16):
where
· 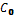 is the initial price of the auction,
is the initial price of the auction, 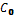
· 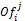 is a offers matrix,
is a offers matrix, 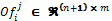 formed by the number of agents i = {1,..., n} plus a row vector AG which shows the winner of each round, and the number of rounds j = {1,
, m}.
formed by the number of agents i = {1,..., n} plus a row vector AG which shows the winner of each round, and the number of rounds j = {1,
, m}.
· 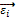 is a vector, where each element represents the maximum amount that each bidder agent i can bid,
is a vector, where each element represents the maximum amount that each bidder agent i can bid, 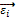 = {
= {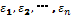 }.
}.
· 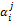 specifies a given proposal, being a the value proposed in the round j, and i the bidder agent.
specifies a given proposal, being a the value proposed in the round j, and i the bidder agent.
· 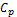 is the condition for stopping the auction and may be of different types:
is the condition for stopping the auction and may be of different types:
· C is the final price of the resource or item, it is the maximum value of the row vector AG (for the case of the Dutch auction it is the minimum), 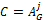 ,
, 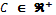 and the winner AG may be any element of the set Ai, i. e.,
and the winner AG may be any element of the set Ai, i. e., 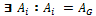 .
.
Figure 1: Interaction protocols
Furthermore the offers matrix (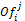 ) stores the proposals of the bidder agents involved and the highest bid (winning bid) made in a given round j by an agent i (winner). Each cell in the matrix contains:
) stores the proposals of the bidder agents involved and the highest bid (winning bid) made in a given round j by an agent i (winner). Each cell in the matrix contains:
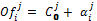 where
where 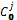 = C0 if j = 1 and
= C0 if j = 1 and 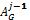 if j > 1
if j > 1
That is, in the first round each cell represents the value of the initial price proposal made by the agent, while in the next rounds that value is the winner value 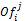 of the previous round j+1, which is
of the previous round j+1, which is 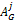 , plus the proposal made by the agent. At the end the row vector AG, identifies the winner in each round.
, plus the proposal made by the agent. At the end the row vector AG, identifies the winner in each round.
The matrix has the following conditions:
· The amount paid by an agent i must be less or equal to the maximum amount that can supply the agent, that is 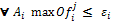 .
.
· For each rows the value proposed by an agent must be greater than its earlier proposal, 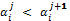
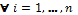 and
and 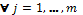 . This applies in case of English auction and One Shut auction, it must be less in case of Dutch auction.
. This applies in case of English auction and One Shut auction, it must be less in case of Dutch auction.
· For any agent in the next round, his proposal should improve the value of the winning bid in the previous round, i. e., 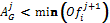 for the case of the English auction. In the case of the Dutch auction the opposite occurs
for the case of the English auction. In the case of the Dutch auction the opposite occurs 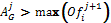 , the value must always be less than the previous
, the value must always be less than the previous 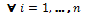 and
and 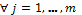 .
.
· In a given round, each proposal for an agent must to improve the previous proposal from another agent. For this we define another matrix, called matrix of order Or, such that 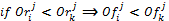 , for the case of the English auction. In the case of the Dutch auction must be
, for the case of the English auction. In the case of the Dutch auction must be 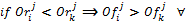 i, k = 1,
, n and
i, k = 1,
, n and 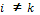 . This matrix
. This matrix 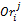 , is a dynamic matrix that indicates the order in which the participants propose their offer in a given round. The dimension of this matrix is i = {1,..., n} agents by j = {1,
, m} rounds.
, is a dynamic matrix that indicates the order in which the participants propose their offer in a given round. The dimension of this matrix is i = {1,..., n} agents by j = {1,
, m} rounds.
The conditions for this matrix are:
· It is not possible simultaneous offers, i. e., 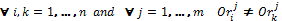
· Any number of order in a given round j must be less or equal to the number of bidders in the auction, i. e., 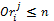 (16).
(16).
The Table 1 summarizes the variables of three auction protocols: English auction, Dutch auction and One Shut auction (the latter protocol, although it does not have a standard model FIPA can be emulated by the contract net protocol of FIPA (11)).
Table 1: Matrix variables auction summary
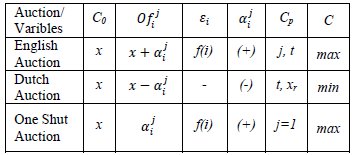
On the Table 1 we can observe that:
1. In the English and Dutch protocols if these exceed a round, C0 value becomes the winner AG of each round.
2. In case of the English auction, 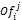 shows a continuous increase while for the Dutch auction it shows a continuous decrease. For the One Shut auction there is only one proposal for each agent.
shows a continuous increase while for the Dutch auction it shows a continuous decrease. For the One Shut auction there is only one proposal for each agent.
3. 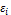 is used only in cases of English Auction and One Shut.
is used only in cases of English Auction and One Shut.
4. In case of the English auction and One Shot 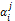 is upward, in the Dutch auction is descending.
is upward, in the Dutch auction is descending.
5. 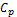 in the English auction, apart of the number of rounds j and time t, it can be when there are not more offers (
in the English auction, apart of the number of rounds j and time t, it can be when there are not more offers (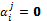 ). For the Dutch auction can be function of the time t, when there are not more offers and/or when it reaches the minimum threshold xr. In the case of One Shut auction is simply based on a single round.
). For the Dutch auction can be function of the time t, when there are not more offers and/or when it reaches the minimum threshold xr. In the case of One Shut auction is simply based on a single round.
6. In case of the English auction and One Shut, C (the final price to be paid) is a maximum value. For the Dutch auction is the smallest value (minimum) of the offers (16).
3.2 Formal Model of the Contract Net Protocol or Tender
Let T be an agent task to be performed at any time. Tj denotes a set of sub-tasks in which T can be divided. A group of agents 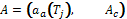 is defined, where
is defined, where 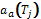 is the manager agent for a sub-task Tj, and AC is the set of agents that can be potential contractors, AC = {A1, A2,
, An}. Furthermore, it is assumed that
is the manager agent for a sub-task Tj, and AC is the set of agents that can be potential contractors, AC = {A1, A2,
, An}. Furthermore, it is assumed that 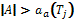 , this ensures that at least two contractors are engaged in the bidding. Finally there will be a
, this ensures that at least two contractors are engaged in the bidding. Finally there will be a 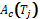 that will be the contractor agent for the task, i. e.,
that will be the contractor agent for the task, i. e., 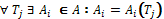 . This protocol can be viewed as a 8- tuple L:
. This protocol can be viewed as a 8- tuple L:
where
· M is the initial message, 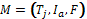 , where Tj is the type of task expecting to be tendered, j={1,
,n}, such that j is the sub-tasks identifier. Ia is the information of the manager agent (it can include its virtual address (DIRa), etc.), and F is the expiration date for offering (it is given by a numeric pair F=[DD,MM], where DD Î{1,31} and DD Î{1,31}).
, where Tj is the type of task expecting to be tendered, j={1,
,n}, such that j is the sub-tasks identifier. Ia is the information of the manager agent (it can include its virtual address (DIRa), etc.), and F is the expiration date for offering (it is given by a numeric pair F=[DD,MM], where DD Î{1,31} and DD Î{1,31}).
· f(Tj) is a function that allows potential contractors to assess their capacities to respond to the notice of request for the performance of the task Tj.
· 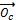 is a vector,
is a vector, 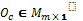 where
where 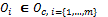 containing the offer of each contractor i to complete the task Tj
containing the offer of each contractor i to complete the task Tj
· g(Oc) is a function that represents the offer evaluation criteria of the manager agent.
· Mp is the message to the winner contractor. It is a tuple 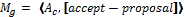 , where Ac is the name of the winner agent, with the communicative act accept-proposal. For the rest of agents, the manager agent diffuses a message that they did not win the bid.
, where Ac is the name of the winner agent, with the communicative act accept-proposal. For the rest of agents, the manager agent diffuses a message that they did not win the bid.
· RP is a vector, 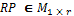 where each cell RPk Î RP represents the progress report k of the agent c winner of the sub-task Tj (for k={1,
,r}).
where each cell RPk Î RP represents the progress report k of the agent c winner of the sub-task Tj (for k={1,
,r}).
· hc(RP,k) is an evaluation function of the manager agent to know the degree of task execution Tj by the contractor.
· RF represents the final report of the winner of the task agent Tj, and it is the last element of vector RP, i. e., RF Î RP .
4 Case Study: Fault Manager System based on Multi-Agent System
The following case study has been taken from the industrial context, where the multi-agents systems becomes a useful technology due to the distributed nature of the process and tasks to be solved in real time. The problem of fault management has been widely studied and several approaches have been proposed. A multi-agent-based approach has been presented in (17), where the coordination model has been addressed by defining the main conversations in order to accomplish the services that the multi-agents system offers. Some of these conversations are very complex. In this work, some part of the conversations defined in (17) will be taken as representative examples to use the proposed formal models. Lets turn now to consider case study. The Fault Management Systems (FMS) is composed of two modules, the first performs the monitoring and failure analysis, and the second performs the tasks of the maintenance management system. The FMS interacts with the Maintenance Engineering and the Fault Tolerant process. The Monitoring and Failure Analysis module includes the fault detection and diagnosis; the Maintenance Tasks module includes the following tasks: Prediction of the occurrence of a functional failure, Planning of preventive maintenance, and execution of maintenance. The FMS is a subsystem of level of supervision of an automated system. Thus, the FMS can be seen as a system composed of intelligent agents that cooperate to solve problems related to the handling of system failures. Furthermore, some activities of the FMS follow a distributed computing model, such as those performed for the fault detection in equipment or processes, the performance index estimation, among others. A specific methodology is used for the specification of the multi-agent system. The methodology provides several models; in this work we will show only a part of the agent model, task model and coordination model. For more details see (17).
Agent Model: the identification of the agents is based on the actors defined in the conceptualization phase. The FMS provides the following functions: monitor, detect, locate, analyze, predict the occurrence of a fault, and correct in the control system. These functions represent the roles of the actors defined in the conceptualization phase as agents, although some of them were divided into several agents. Thus, there are eight agents (17): Detector Agent (it is a special Agent), Locator Agent (it is a special Agent), Diagnoser Agent (it is a special Agent), Predictor Agent (it is a special Agent), Coordinator Agent, Controller Agent, Actuator Agent (it is a special Agent), Observer Agent. Specialized Agents and Coordinator Agent belong to the Supervisor level, and the Controller, Observer and Actuator agents belong to the Process level. The detailed specification of these agents is in (17). In addition, the FMS interacts with the control process based on SCDIA through a Middleware (MGS, for its acronym in Spanish), composed by the next agents: Database Agent, Agents Manager Agent, among others.
Task Model: The following Table 2 shows the task model of the FMS. Each task is divided in sub-tasks and each sub-task is identified with a particular type. This identification is used to the instantiation of the contract net protocol later. Table 2 provides two major advantages, the first is that it defines a large type of tasks and sub-tasks (all are identified by their initials in Spanish), and the second is that it allows state the skills that must have the agents to perform such tasks or subtasks (third column).
Coordination Model: In this example, two particular conversations are taken: Urgent Tasks and On-condition Maintenance (more conversations are presented in (17)). Specifically, the conversation Urgent Tasks is taken to model the English auction mechanism by using the formalism. This conversation is shown in Figure 2a).
Table 2: Tasks, Sub-tasks and Sub-tasks Type
Conversation: Urgent Tasks
· Objective: To perform urgent tasks in the system.
· Interacting agents: Coordinator (Acoo), Controller (Acon), Database (ABD), Actuator (AA), Observer (AO) and Human (AH).
· Beginner: Coordinator Agent
· Speech Acts: Rush orders, Maintenance Order, Report of Maintenance, Alarm.
· Precondition: Have to make urgent tasks in the system.
· Ending condition: If the urgent task is not made a given alarm is generated.
· Description: The coordinator agent sends information to the controller agent, with the maintenance order, and if it could make this urgent task it sends an alarm.
The conversation On-condition Maintenance is taken to model the contract net protocol because there are agents and requirements that may be associated with tendering scenarios (see Figure 2 (b)).
Conversation: On- condition Maintenance
· Objective: Perform maintenance tasks on the system.
· Interacting agents: Coordinator (Acoo), Controller (Acon), Database (ABD), Detector (AD), Pager (AL), Predictor (AP), Diagnosers (ADi) and Human (AH)
· Beginner: Controller Agent
· Speech Acts: Order of service, Order of Detection, Get Process Information, Historical View, Search, Order of Execution, Localization, Diagnostic Order, Prediction Order, Alarm and Submit a Maintenance Plan
· Precondition: Have to do a service
· Ending Condition: Coordinator agent sends plan of maintenance.
· Description: Through this conversation the controller agent sends information to the Coordinator for building the maintenance plan.
4.1 English Auction for Urgent Task Conversation
It is proposed the following scenario: there are four (4) plants grouped in a production unit operated by a single coordinator agent of a production unit. In addition, each plant that integrates this unit has a database agent that stores pending maintenance tasks of each plant. On the other hand, there are limited resources to perform maintenance tasks, so database agents must "compete" with each other for a place in the list of urgent tasks of the Coordinator, which would have a finite buffer of tasks to execute in a period of time. This process of competition can be viewed as an auction, where the agent auctioneer is the Coordinator agent, Database agents would be the bidders and the item offered is a place for the execution of urgent tasks. The model has the following values:
· Beginner agent (as): Coordinator agent (auctioneer agent)
· Interacting agents Ai = {A1, A2, A3, A4}, 4 Data Base agents (bidders agents).
· Initial price: C0 = x, and each cell is
· 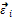 ={ ε1, ε 2, ε 3, ε 4}. For this particular case we call to
={ ε1, ε 2, ε 3, ε 4}. For this particular case we call to 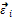 needs of each agent.
needs of each agent.
· Stop condition, Cp = j > 1 and 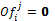 , i. e., it occurs after the first round and when there are not more bids.
, i. e., it occurs after the first round and when there are not more bids.
· Ascending auction (English Auction).
· An example of the offers matrix Of and the order matrix Or is shown in Table 3 and Table 4.
Table 3: Example of offers matrix Of
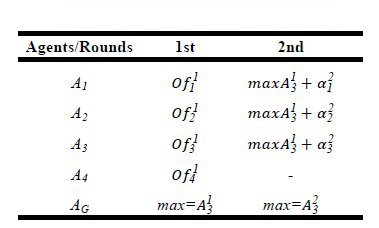
Table 4: Example of order matrix Or
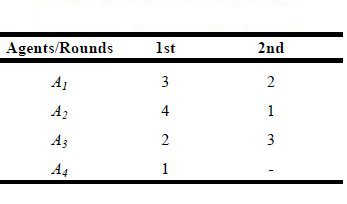
Table 3 and Table 4 show that:
· In the first round the agent three bids in the second order and suggested the highest value ( Table 4 and Table 3).
· The agent four does not bid in the second round.
· The last element of row vector AG shows that the winner is the database agent three.
· The price that must to pay the database agent 3 is C = max 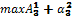 and has the preference of the Coordinator to perform its urgent tasks.
and has the preference of the Coordinator to perform its urgent tasks.
Figure 3: Interaction Diagram for an English Auction for the Urgent Tasks Conversation
4.2 Contract Net Protocol for On-Condition Maintenance Conversation
For this case it is used the conversation of Maintenance On-Condition Maintenance from the FMS (17). The case study is a subsystem of pumping in a specific area. The subsystem has the following equipment: main pump, main filter, blocking filter, electromechanical timers, pipes and valves. At one point, the controller agent sends a request to Coordinator agent to perform a diagnostic task of three equipment of the pumping subsystem: main pump, electromechanical timers and valves, within a specific date. After this request is sent by the controller agent, given the magnitude of the task, coordinators agent sends three offers (a broadcast message) to a group of Diagnoser agents. This message is answered by several Diagnoser agents. This scenario can be seen from the perspective of a contract net in which the Coordinator agent would be the manager agent of the diagnostic task of the three equipments, and the existing Diagnoser agents will be potential contractors. Figure 4 shows the part of the conversation (red box) where this mechanism will be used (in which the previous scenario is described) in the conversation of On-Condition Maintenance. The possible bidding process using the formalism is:
· Types of tasks: three diagnostic tasks, TDi1 (main pump), TDi2 (timers), TDi3 (valves)
· Three Manager agents (aa): One Coordinator Agent (ACoo1, ACoo2, ACoo3) for each task.
· Potential contractors for the tasks: for TDi1 Ac={A11,A12,A13,A14}, for TDi2 Ac={A21,A22,A23}, and for TDi3 Ac={A31,A32,A33,A34,A35} all diagnoser agents. For each agent the first index represents the task and the second the number of the agent.
· Initial Message: M=(TDi, DIRa, [DD,MM])
· f(TDij), function to evaluate the ability to do a task by the contractors (determines if it will offer). As criteria for offer evaluation they consider their skills and availability.
Table 5 , Table 6 and Table 7 show the agents skills (the nomenclature EC, TS, TPO and TB are taken from Table 2, third column)
· g(Oc), is the criterion of evaluation of offers by the manager agent. We assume as evaluation criterion the availability of time of each agent to perform the task.
· Messages for the winners (MP):
Table 8: Messages for the winners of each task TDij
· The vector RP of each task TDij
Table 9: Parcials report of each task TDij
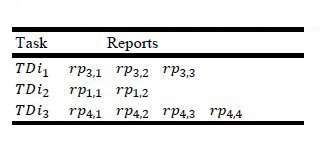
Each report has two indexes, the first is the number of the agent and the second the number of the reports.
· h(RP,k) is the function that evaluates the performance of each contractor agent in each task for which it was hired, such that each vector RP corresponds to the task TDij in evaluation
· The value RF for each vector RP of each TDij could be:
In summary, we have:
· The number of agents offering to each one of the tasks (according to the function f(TDij)) were: for TDi1 = 4 agents ( Table 5), TDi2 = 3 agents ( Table 6), TDi3 = 5 agents ( Table 7), They are diagnosers.
· Table 8 shows that each manager evaluates the offers received, leaving as winners: Agent 3 for TDi1, agent 1 for TDi2 and agent 4 for TDi3, which are assumed to have immediate availability.
· For vectors of partial reports ( Table 9), we see that the agent 4 reports more progress in its assigned task (four times).
· Finally, they get the final report with the diagnosis of each one of the equipment requested in the task.
Figure 4: Part of the Conversation where we apply the tender mechanism
4.3 Conclusions
The auction and contract net mechanisms have been used in many applications of computer science that involve the allocation of goods, tasks and resources. The formalization of these mechanisms by using mathematical models allows a representation in their different forms (English auction, Dutch auction, etc.). This is important because we can generalize the description of these protocols, this is very important when trying to optimize their utilization in a given context. The cases of study allow validate both models. The formals models can describe the particular cases of coordination mechanisms that are treated in this work, we can easily characterize the scenarios where they want be used. This article is essential for future works, which have the goal to propose an optimization model of coordination schemes for communities of agents using cultural algorithms. This optimization model is a multi-agent learning mechanism. Specifically, the coordination mechanisms that have been formalized with our models can be manipulated by the evolutionary process of the cultural algorithms. Thus, having the models for the expected coordination mechanisms for multi-agent systems (e. g., planning, emergent coordination, etc.), the optimization process will determine the appropriate coordination schemes of a given agents community.
Acknowledgements
Thanks to the I-1237-10-02-AA Project of the CDCHT of the Universidad de Los Andes and 2994 Project of the Programa de Estímulo a la Investigación of FONACIT for the financial support.
References
(1) H. Nwana, L. Lee, N. Jennings, Co-ordination in software agent systems. BT Technol J, Vol. 14, no. 4, October 1996.
(2) J. Ferber LES SYSTÈMES MULTI-AGENTS. Vers une intelligence collective. InterEditions, 1995.
(3) S. Koenig, P. Keskinocak, C. Tovey. Progress on Agent Coordination with Cooperative Auctions. Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence, Atlanta, Georgia, USA, July 11-15, 2010.
(4) Zheng X., and Koenig S. Sequential Incremental-Value Auctions. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), 2010.
(5) S. Koenig, X Zheng, C. Tovey, R. Borie, P. Kilby, V. Markakis, and P. Keskinocak. Agent Coordination with Regret Clearing. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), 101-107, 2008.
(6) P. Vytelingum, S. Ramchum, T. Voice, A. Rogers, and N. Jennings. Trading agents for the smart electricity grid. In The Ninth International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2010), pages 897–904, May 2010.
(7) D. Sun and J. Wu, Multi-agent Coordination Based on Contract Net Protocol, Proceeding IUCE '09 Proceedings of the 2009 International Symposium on Intelligent Ubiquitous Computing and Education. Pages 353-357.
(8) T. Logenthiran, D. Srinivasan, D. Wong, Multi-agent coordination for DER in MicroGrid, Sustainable Energy Technologies, ICSET. IEEE International Conference on Nat. Univ. of Singapore, Singapore, pp. 77-82, 2008.
(9) F. Brandt, W. Brauer, G. Weib, Task Assignment in Multiagent Systems based on Vickrey-type Auctioning and Leveled Commitment Contracting.
(10) FIPA English Auction Interaction Protocol Specification, Document number: XC00031F. Approved for Experimental: 2001/01/29.
(11) FIPA Contract Net Interaction Protocol Specification, Document number: SC00029H. Approved for Standard 2002/12/03.
(12) M. Wooldridge, An Introduction to Multi Agent Systems, Department of Computer Science, University of Liverpool. WILEY & SON, LTD. Copyright 2002.
(13) M. A. Espinosa and F. Lopez, Diseño de Sistemas Multiagentes. Tesis de Grado. Facultad de Ciencias de la Computación. Benemérita Universidad Autónoma de Puebla. 2006.
(14) R. Smith, The Contract Net Protocol: High-Level Communication and Control in a Distributed Problem Solver, IEEE Transactionson on Computers, Vol. C-29, no. 12, December 1980.
(15) C. La Fournie, Cooperations using Negotiations and the Contract Net Protocol. pages.cpsc.ucalgary.ca/~laf/601.72/Negotiaion&ContractNet.pdf.
(16) J. C. Terán, J. L. Aguilar and M. Cerrada, Formalización del Mecanismo de Subasta para la Coordinación de Sistemas Multi-Agentes. II Simposio Científico y Tecnológico en Computación. Escuela de Computación, Universidad Central de Venezuela, pp.114-121, Mayo 2012.
(17) M. Cerrada , J. Aguilar, J. Cardillo, R. Faneite, Agents-based design for fault management systems in industrial processes, Journal Computers in Industry, 2007, Vol. 58, no. 4, pp. 313-328.
(18) J. L. Aguilar, M. Cerrada, G. Mousalli, F. Rivas, F. Hidrobo, A Multiagent Model for Intelligent Distributed Control Systems, Lecture Notes in Artificial Intelligence, Springer-Verlag, Vol. 3681, pp. 191-197, 2005.