Services on Demand
Journal
Article
Related links
Share
CLEI Electronic Journal
On-line version ISSN 0717-5000
CLEIej vol.15 no.3 Montevideo Dec. 2012
Abstract
In this work we study coupled incompressible viscous flow and advective-diffusive transport of a scalar. Both the Navier-Stokes and transport equations are solved using an Eulerian approach. The SUPG/PSPG stabilized finite element formulation is applied for the governing equations. The implementation is held using the libMEsh finite element library which provides support for parallel adaptive mesh refinement and coarsening. The Rayleigh-Bénard natural convection and the planar lock-exchange density current problems are solved to assess the adaptive parallel performance of the numerical solution.
Portuguese abstract
Nesse trabalho nós estudamos o escoamento incompressível de fluidos viscosos e o transporte advectivo-difusivo de um escalar. As equações de Navier-Stokes e do transporte são resolvidas usando um esquema Euleriano. A formulação estabilizada SUPG/PSPG do método dos elementos finitos é aplicada às equações governantes. A implementação é realizada utilizando a biblioteca de elementos finitos libMesh que fornece suporte para refinamento/desrefinamento adaptativo de malhas em paralelo. Os problemas de convecção natural de Rayleigh-Bénard e de corrente gravitacional em configuração lock-exchange plana são resolvidos para avaliar o desempenho da solução numérica paralela e adaptativa.
Keywords: Stabilized FEM formulation, incompressible flows, adaptive meshes, parallel computing.
Formulação estabilizada do MEF, escoamentos incompressíveis, malhas adapatativas, computação paralela
Received: 2012-06-10 Revised 2012-10-01 Accepted 2012-10-04
The numerical simulation of current engineering problems would not be feasible without the advent of parallel computing. Even with the development of techniques for mesh adaptation, the fastest available processors are not able to solve, within a practical period of time, problems that have large amounts of degrees of freedom. High-performance computing (HPC) have enabled the solution of problems with a large number of unknowns and high complexity (often involving multiple scales and multiple physics) by clusters of computers installed in universities as well in industry research centers.
To make HPC be efficiently used, a set of algorithms and computational methods have been developed over the last decade that made possible high fidelity solutions of complex problems. Processors with multiple cores with shared memory, clusters of personal computers in which each processor has its own memory (distributed memory) and more recently, the hybrid memory architectures are present on the daily work of engineers and researchers.
Although improving processing capacity, parallel computation have added complexity to computer codes programing. According to (1) scaling performance is particularly problematic because the vision of seamless scalability cannot be achieved without having the applications scale automatically as the number of processors increases. However, for this to happen, the applications have to be programmed to exploit parallelism efficiently. Therefore, parallel computing resources should be used rationally in order to obtain compatible performances.
Good simulation practice suggests that the applications and algorithms employed in HPC should be optimized for this purpose. Currently there are available (mostly freely distributed) several programs to perform different tasks inherent to parallel computing. The domain partitioning and load balancing, information exchange between processors, algebraic operations and linear preconditioned systems solving are some of the necessary operations and have specific computational libraries that can be incorporated into the implementation of a numerical simulator.
In order to keep the focus on the issues related to the numerical problem, we use the libMesh framework, which is a C++ library for parallel adaptive mesh refinement/coarsening numerical multiphysics simulations based on the finite element method (2). The library has been developed since 2002 by a group of researchers from CFDLab, Department of Aerospace Engineering and Engineering Mechanics, University of Texas at Austin, and is available as open source software (http://libmesh.sourceforge.net/).
In this work we implement stabilized finite element formulations for the Navier-Stokes and advective-diffusive transport in libMesh. Parallel adaptive simulations of coupled problems confirm the mesh size reduction potential and the ability to capture the solution small scales as well the development of the interface between the fluids in evolution problems.
The remainder of this work is organized as follows. In the next section the dimensionless governing equations for the coupled viscous flow and transport is presented together with correspondent stabilized SUPG/PSPG finite element method (FEM) formulation. Details of the adaptive mesh refinement/coarsening (AMR/C) in the context of the libMesh library as well some aspects of the parallel solution of precondiotioned linear systems are presented in Section 3. Section 4 presents the results of the parallel adaptive simulation of the Rayleigh-Bénard natural convection and a density current in a planar lock-exchange configuration. The paper ends with the main conclusions.
Assuming an unsteady incompressible viscous flow and the Bousinessq approximation, the dimensionless Navier-Stokes, continuity and scalar transport equations (details on how the physical quantities may be normalized in order to arrive at dimensionless equations can be found at (3)) can be written in a non conservative form following a Eulerian description as
![∂u- -1- 2 -Gr- ∂t + u∇u - Re ∇ u+ ∇p = Re2 ϕe in Ω ×(0,t],](/img/revistas/cleiej/v15n3/3a020x.png) | (1) |
![∇ ⋅u = 0 in Ω × (0,t],](/img/revistas/cleiej/v15n3/3a021x.png) | (2) |
![∂ϕ-+ u⋅∇ ϕ- -1∇2 ϕ = 0 in Ω × (0,t]. ∂t D](/img/revistas/cleiej/v15n3/3a022x.png) | (3) |
defined in the simulation domain 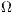 with a smooth boundary
with a smooth boundary 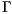 . The time is
. The time is 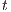 ,
, 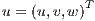 is the velocity field,
is the velocity field, 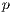 is the pressure and
is the pressure and 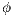 the scalar being transported and
the scalar being transported and 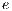 is an unit vector aligned with the gravity.
is an unit vector aligned with the gravity.
In (1) 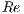 and
and 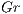 are the Reynolds and Grashof numbers. The inverse of the parameter
are the Reynolds and Grashof numbers. The inverse of the parameter 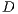 in equation (3) represents a dimensionless diffusive constant depending on the nature of the scalar being transported (e.g., the Peclet number for the temperature transport).
in equation (3) represents a dimensionless diffusive constant depending on the nature of the scalar being transported (e.g., the Peclet number for the temperature transport).
The essential and natural boundaries conditions (BCs) are:
![( u] = g on Γ g, 1--( T) n⋅ Re ∇u + (∇u ) - pI = h on Γ σ, ϕ = ϕ- on Γ , ( ) ϕ - n ⋅-1∇ ϕ = q on Γ q D](/img/revistas/cleiej/v15n3/3a0213x.png) | (4) |
where 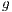 and
and 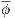 are functions with prescribed values for the velocity vector and scalar defined on the regions
are functions with prescribed values for the velocity vector and scalar defined on the regions 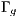 and
and 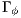 of the boundary where the essential BCs are imposed. Furthermore
of the boundary where the essential BCs are imposed. Furthermore 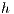 and
and 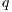 represent the natural BCs acting on the regions
represent the natural BCs acting on the regions 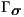 and
and 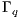 . Generally
. Generally 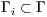 .
. 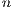 is the unit outward normal vector on the boundary and
is the unit outward normal vector on the boundary and 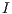 is the
is the 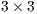 identity matrix.
identity matrix.
The initial conditions are:
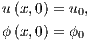 | (5) |
where the initial velocity field 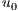 is divergent free.
is divergent free.
In gravity current problems, the concept of buoyancy velocity 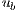 is largely used (see (4)). It may be defined as
is largely used (see (4)). It may be defined as
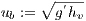 | (6) |
where 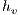 is a scale length related to the vertical dimension of the simulation domain (usually taken as the domain height) and
is a scale length related to the vertical dimension of the simulation domain (usually taken as the domain height) and 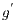 is called the reduced gravity given by
is called the reduced gravity given by
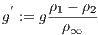 | (7) |
where 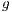 is the absolute value of the gravitational acceleration,
is the absolute value of the gravitational acceleration, 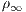 is the reference density,
is the reference density, 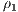 is the density of the “heavy” fluid and
is the density of the “heavy” fluid and 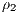 is the density of the “light” fluid.
is the density of the “light” fluid.
When one uses the buoyancy velocity as a reference velocity and 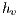 as the scale length, the Reynolds number may be computed directly from the Grashof as follow
as the scale length, the Reynolds number may be computed directly from the Grashof as follow
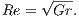 | (8) |
For particle-driven problems (a class of gravity current phenomenon), where the transported scalar is the density 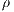 , the diffusivity constant is given by the product of the Schmidt
, the diffusivity constant is given by the product of the Schmidt 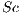 and Grashof numbers. Taking it into account, the Navier-Stokes and advective-diffusive equations may be rewritten as
and Grashof numbers. Taking it into account, the Navier-Stokes and advective-diffusive equations may be rewritten as
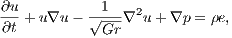 | (9) |
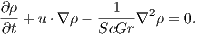 | (10) |
2.2 Stabilized Finite Element Formulation
Given a suitably defined finite-dimensional trial solution and weight functions spaces for velocity and pressure
![{ ( ]3 } Shu = uh | uh ∈ H1h (Ω ) , uh=.gh em Γ g , { ( ]3 . } Vhw = wh | wh ∈ H1h (Ω) , wh = 0 em Γ g , Sh = Vh = {qh | qh ∈ H1h(Ω )} p p](/img/revistas/cleiej/v15n3/3a0243x.png) | (11) |
where 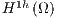 is the finite-dimensional space function square integrable into the element domain, the stabilized SUPG/PSPG FEM formulation for the non-dimensional Navier-Stokes and continuity equations (1) and (2) can be written as: Find
is the finite-dimensional space function square integrable into the element domain, the stabilized SUPG/PSPG FEM formulation for the non-dimensional Navier-Stokes and continuity equations (1) and (2) can be written as: Find 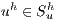 and
and 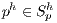 such as,
such as, 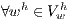 and
and 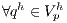 ,
,
![∫ h ((∂uh h h) h] 1 ∫ ( h)T h w ⋅ -∂t-+ u ∇u - l dΩ+ Re- ∇w ⋅∇u IdΩ- ∫Ω ∫ ∫ Ω ∇whphId Ω - wh ⋅hhdΓ + qh∇ ⋅uhdΩ+ Ω Γ (( Ω ) ] n∑el ∫ ( h h) ∂uh- h h h h e Ωe τSUPGu ∇w ⋅ ∂t + u ∇u + ∇p - l dΩ + e=1 ∫ (( ) ] n∑el ( h) ∂uh- h h h h e Ωe τPSPG∇q ⋅ ∂t + u ∇u + ∇p - l dΩ = 0. e=1](/img/revistas/cleiej/v15n3/3a0249x.png) | (12) |
The first four integrals in (12) arise from the classical Galerkin weak formulation for the Navier-Stokes equations. The fifth integral represents the classical Galerkin formulation for the continuity equation. The summations over the elements are the SUPG and the PSPG stabilizations for the Navier-Stokes equation. The parameters adopted for both stabilizations were obtained from (5) and are defined as follows
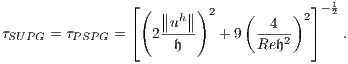 | (13) |
The dimensionless stabilizations parameters are local (element level) so, the velocity modulus 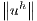 is calculated for each element
is calculated for each element 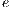 and
and 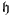 is an element length measure based in its volume
is an element length measure based in its volume 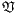 as shown bellow
as shown bellow
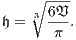 | (14) |
The discretized dimensionless body force are represented by 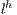 .
.
For the dimensionless advective-diffusive transport we adopt the same assumptions, so given the following finite-dimensional trial solution and weight functions spaces for the scalar
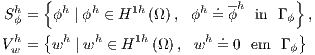 | (15) |
the stabilized FEM formulation can be written as: Find 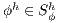 such as,
such as, 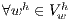 ,
,
![∫ ( h ) ∫ ( ) ∫ wh ⋅ ∂-ϕ-+ uh ⋅∇ϕh dΩ + 1- ∇wh T ⋅∇ ϕhdΩ - whqdΓ + Ω ∂t D Ω Γ ∑nel ∫ ( h h) ((∂ ϕh h h) ] e e τSUPGu ⋅∇w ⋅ -∂t-+ u ⋅∇ϕ dΩ = 0. e=1 Ω](/img/revistas/cleiej/v15n3/3a0260x.png) | (16) |
The three first integrals in (16) come from the Galerkin weak formulation. The integral into the summation over the elements is the SUPG stabilization. The non-dimensional stabilization parameter is computed similarly to (13), that is:
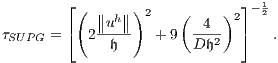 | (17) |
In the stabilized formulations (16), an additional stabilization is added to handle instabilities in the numerical solution of flows with presence of strong gradients of the scalar being transported. In (6) is presented a discontinuity capturing term which is calculated as follows:
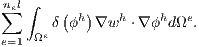 | (18) |
Because the 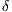 parameter is a function of the scalar, (16) can be understood as a nonlinear diffusion operator. In this work, the
parameter is a function of the scalar, (16) can be understood as a nonlinear diffusion operator. In this work, the 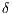 parameter was adapted from (6) as follows in dimensionless form
parameter was adapted from (6) as follows in dimensionless form
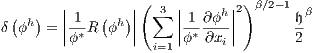 | (19) |
where 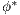 is a dimensionless value of the scalar (usually taken as 1) and
is a dimensionless value of the scalar (usually taken as 1) and 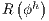 is an approximation for the actual residual defined as:
is an approximation for the actual residual defined as:
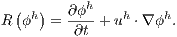 | (20) |
The 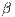 parameter can be set as 1 or 2.
parameter can be set as 1 or 2.
Adopting the implicit backward Euler scheme for the time discretization together with a fixed point linearization, the final discrete system of (12) and (16) results in
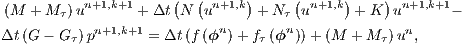 | (21) |
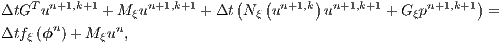 | (22) |
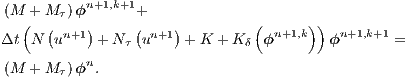 | (23) |
In the matrix systems (21), (22) and (23) 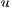 ,
, 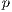 and
and 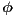 are the nodal vectors of the correspondent unknowns
are the nodal vectors of the correspondent unknowns 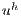 ,
, 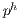 and
and 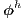 , and
, and 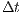 stands for the time-step size. The super indexes
stands for the time-step size. The super indexes 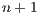 and
and 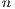 mean the current and previous time-steps while
mean the current and previous time-steps while 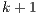 and
and 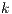 are respectively the current and previous nonlinear iterations counter.
are respectively the current and previous nonlinear iterations counter.
For the matrices where the advective operator appears, i.e., Galerkin advection, SUPG mass and advection, and PSPG advection, the velocity components are evaluated at each integration point. 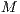 is the mass matrix,
is the mass matrix, 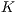 is the viscous/diffusive matrix,
is the viscous/diffusive matrix, 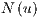 is the nonlinear advection matrix,
is the nonlinear advection matrix, 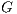 and
and 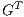 are the gradient and its transpose (divergent) matrices.
are the gradient and its transpose (divergent) matrices. 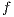 is the body force vector.
is the body force vector. 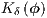 is the nonlinear discontinuity capturing matrix. The matrices and vectors with the subscripts
is the nonlinear discontinuity capturing matrix. The matrices and vectors with the subscripts 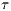 and
and 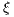 mean the SUPG and PSPG terms.
mean the SUPG and PSPG terms.
The mesh adaptivity together with high-performance computing (parallel processing) play a key role to enable numerical simulations of actual engineering/industrial problems within an acceptable time without exhausting the processing capacity of current computers.
Particularly for the density current problem, AMR/C is a important tool to capture and track the flow structure at the front, where the Kelvin-Helmholtz billows occur. From an initial coarse mesh, the adaptivity refinement process begins near the interface between the two fluids and it follows its development.
In libMesh the mesh refinement can be accomplished by element subdivision (h-refinement), increasing the local polynomial degree (p-refinement) as well a combination of both methods (hp-refinement). Although there is an extensive literature devoted to obtaining reliable a posteriori estimators that are more closely linked to the operators and governing equations (7, 8), in libMesh the error indicator is focused on local indicators that are essentially independent of the physics (2).
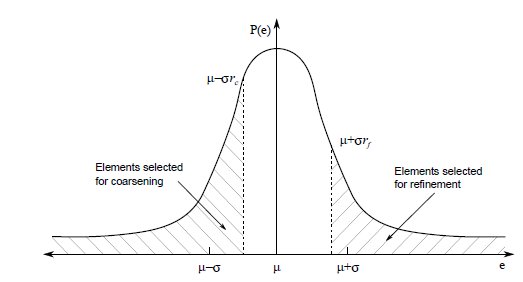
libMesh uses a statistical refinement/coarsening scheme based on the ideas presented in (9) where the mean 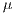 and the standard deviation
and the standard deviation 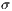 of the error indicator “population” are computed. Using refinement and coarsening fractions (
of the error indicator “population” are computed. Using refinement and coarsening fractions (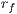 and
and 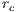 ), the elements are flagged for refinement and coarsening as showed in Fig. (1).
), the elements are flagged for refinement and coarsening as showed in Fig. (1).
This scheme is suitable for evolution problems where, in the beginning, a small error is evenly distributed. Throughout the simulation the error distribution spreads and the AMR/C process starts. Whether the solution approaches its steady-state, the distribution of error also reaches the steady-state, stopping the AMR/C process.
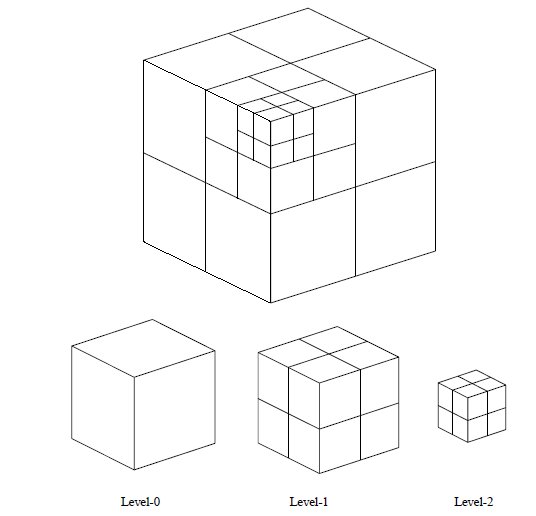
The elements are refined through a “natural refinement” scheme: elements of dimension 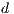 , with the exception of the pyramids, produce
, with the exception of the pyramids, produce 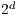 elements of the same type after refinement. The degrees of freedom are constrained at the hanging nodes on element interfaces. This approach yields a tree data structure formed by the “parents” and their “children” elements. An example of an element level hierarchy resulting from the application of this scheme for a hexahedral mesh is presented in Fig. 2.
elements of the same type after refinement. The degrees of freedom are constrained at the hanging nodes on element interfaces. This approach yields a tree data structure formed by the “parents” and their “children” elements. An example of an element level hierarchy resulting from the application of this scheme for a hexahedral mesh is presented in Fig. 2.
The elements present in the initial mesh (level-0 elements) have no parents as well the active elements (those that are part of the current simulation mesh) have no children, so the latter are the current high-level elements. The element level is determined recursively from its parents and the user should determine the maximum refinement level.
The frequency of refinement/coarsening is an user’s responsibility. When the mesh adapts it is optimized for the state at the current time (10). One should find a frequency of adaptivity which will balance the computational effort and quality of results as there is a computational cost associated with the adaptivity process. When the mesh is adapted, the field solution should be projected (interpolated) and a simulation should be performed on the new mesh.
In this work we use a class of errors estimators based on derivative jump (or flux jump) of the transported scalar calculated at the elements interface called Kelly’s Error Estimator (11) to perform the h-refinement. The refinement and coarsening fractions for the statistical strategy as well the adaptivity frequency are set independently for each simulation problem.
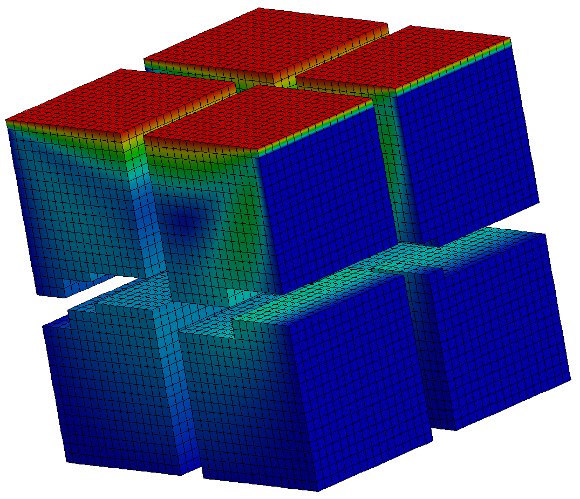
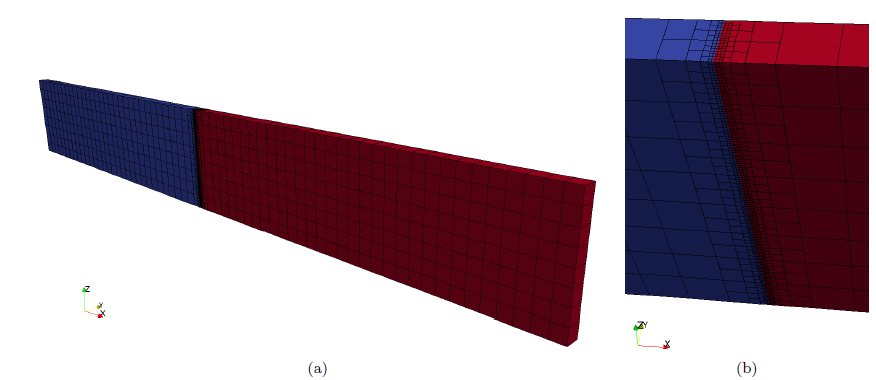
In this paper, we consider the standard partitioning domain without overlap, as shown in Fig. (3), where the elements related to each of the sub-domains are assigned to different processors. That is, the simulation domain 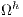 is divided into a discrete set of sub-domains
is divided into a discrete set of sub-domains 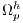 such as
such as 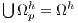 and
and 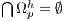 .
.
In AMR/C computations at a new adaptation stage, regions of the domain will have an increase in mesh element density while in others, the number of elements will decrease. These dynamic mesh adjustments result for some processors in significant increasing (or decreasing) work therefore causing load unbalancing (1).
Libraries such as METIS and ParMETIS were developed aiming implementing efficient partitioning mesh schemes. The first is a serial mesh partitioning library, while the second is based on parallel MPI. Both can also reorder the unknowns in unstructured grids to minimize the fill-in during LU factorization. The ParMETIS extends the functionality provided by METIS and includes routines for parallel computations with adaptive meshes refinement and large-scale numerical simulations.
3.3 Parallel Solution of Preconditioned Linear Systems
The support for the numerical solution of the resulting system of linear equations in the parallel architecture environment is provided by PETSc. It provides structures for efficient storage (vectors, arrays, for example), as well ways to handle it. The libMesh uses compressed sparse row (CSR) data structure to store the sparse matrices. PETSc has a number of methods for solving linear sparse system as GMRES and BiConjugate Gradient method (BiCG) and several types of preconditioners as ILU(k) and Block-Jacobi. Options for reordering the linear system as the Reverse Cuthill-McKee method (RCM, (12)) are also available.
In this work we use Block-Jacobi sub-domain preconditioning. It is one of the most widely used schemes due to its easiness of implementation. There are no overlap between the blocks. The incomplete factorization may be applied to each of them without extra communication costs. However, in adaptive simulations, the new local factorization should be performed every time the mesh is modified since the adaptivity changes the group of elements residing in each sub-domain (13). It is usual to refer to the Block-Jabobi preconditioning strategy in conjunction with the ILU factorization with a certain level 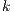 of fill-in by BILU(
of fill-in by BILU(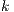 ) (14).
) (14).
The communication between the processors, such as required for the algebraic operations or during assembly of arrays of elements are supported by a set of PETSc library routines which is designed for parallel computing using the MPI API.
The simulations were performed in a SGI Altix ICE 8400 cluster with 640 cores (Intel Nehalem). This machine has 1.28 TB of distributed memory. The processing nodes are connected by InfiniBand. The cluster is located at the High-Performance Computing Center (NACAD) of the Federal University of Rio de Janeiro, Brazil.
4.1 Parallel Adaptive Simulation of the Rayleigh-Bénard Problem
In this example we consider the Rayleigh-Bénard natural convection in a container with geometric domain ![Ω = (0,4]× (0,1]× (0,1)](/img/revistas/cleiej/v15n3/3a02105x.png) . This problem consists to solve a natural convection phenomenon of a fluid which initially at rest (
. This problem consists to solve a natural convection phenomenon of a fluid which initially at rest (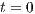 ) produces a sequence of adjacent convection cells along the longitudinal direction (
) produces a sequence of adjacent convection cells along the longitudinal direction (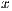 axis) due to the temperature difference between its upper (cold) and lower (hot) walls.
axis) due to the temperature difference between its upper (cold) and lower (hot) walls.
No-slip boundary conditions are imposed in all the walls and the pressure is prescribed as 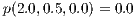 . The dimensionless cold temperature is
. The dimensionless cold temperature is 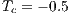 and the hot
and the hot 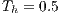 . The physical problem is defined setting the Reynolds Number as
. The physical problem is defined setting the Reynolds Number as 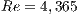 , Grashof number as
, Grashof number as 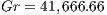 , the Peclet number as
, the Peclet number as 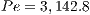 and Froude number (besides not introduced in the Navier-Stokes equations presented in section 2.1, the Froude number is used here to take into account the fluid’s weight in the calculation. More details about how to incorporate the Froude number in the dimensionless Navier-Stokes equations may be found in (3).) as
and Froude number (besides not introduced in the Navier-Stokes equations presented in section 2.1, the Froude number is used here to take into account the fluid’s weight in the calculation. More details about how to incorporate the Froude number in the dimensionless Navier-Stokes equations may be found in (3).) as 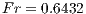 .
.
Only one refinement/coarsening level was allowed at every 25 time-steps. For the statistical adaptivity scheme the refinement fraction is 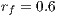 and coarsening fraction is
and coarsening fraction is 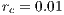 . The linear tolerance for GMRES(30) together with the BILU(
. The linear tolerance for GMRES(30) together with the BILU(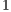 ) and reordering by RCM method is
) and reordering by RCM method is 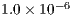 . The nonlinear tolerance is
. The nonlinear tolerance is 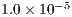 and the constant time step size is
and the constant time step size is 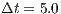 .
.
The steady-state velocity vectors are shown in Fig.(4) and the temperature over the final adapted mesh is plotted in Fig.(5).
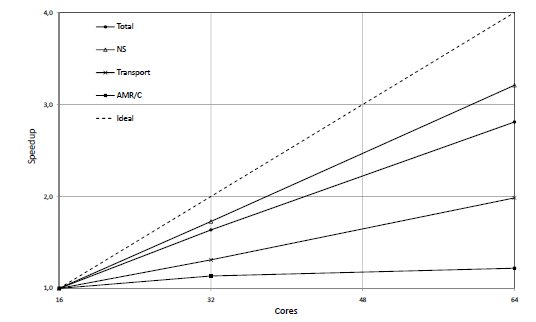
The Fig. (6) presents the speedup for the total simulation time, the total time for solving the Navier-Stokes and transport problems and the AMR/C procedure considering in the numerator the time spent with 16 CPU’s, i.e.,
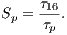 | (24) |
The AMR/C time does not reach 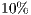 of the total simulation time. We may observe from the results of Fig.(6) that the present simulation achieves a good parallel performance, that is, speed up around 3 for the total simulation with 64-cores run with respect to 16-cores run (over 3 for the Navier-Stokes simulation).
of the total simulation time. We may observe from the results of Fig.(6) that the present simulation achieves a good parallel performance, that is, speed up around 3 for the total simulation with 64-cores run with respect to 16-cores run (over 3 for the Navier-Stokes simulation).
Despite the good overall performance, it is observed that the adaptive procedure does not scale as well as the linear solvers (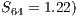 . The poor performance of the AMR/C procedure in the current libMesh release is due to the fact that all mesh data are replicated on all cores, which increases memory requirements and communication per core.
. The poor performance of the AMR/C procedure in the current libMesh release is due to the fact that all mesh data are replicated on all cores, which increases memory requirements and communication per core.
4.2 Temperature-driven gravity current with AMR/C
For the simulation of a temperature-driven gravity current with mesh adaptivity, we consider a slice domain (to emulate a 2D simulation domain from a mesh composed of 3D elements, the slice domain is positioned parallel to the 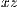 plane and the perpendicular direction
plane and the perpendicular direction 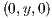 is discretized with only one element except at regions where the mesh adapts. For all nodes on the mesh
is discretized with only one element except at regions where the mesh adapts. For all nodes on the mesh 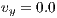 is imposed.)
is imposed.) 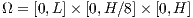 where the nondimensional length and height are
where the nondimensional length and height are 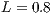 and
and 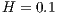 . The left half of the channel is initially filled with the cold fluid and the right half is filled with hot fluid. The Fig. (7) shows the initial configuration and a detail of the refinement at the center of the domain.
. The left half of the channel is initially filled with the cold fluid and the right half is filled with hot fluid. The Fig. (7) shows the initial configuration and a detail of the refinement at the center of the domain.
The dimensionless cold temperature is set to 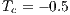 and the hot
and the hot 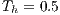 . We consider no-slip boundary conditions on the bottom, left and right walls. Free-slip boundary conditions are imposed on the top one. Thus free and no slip fronts may be considered in the same simulation.
. We consider no-slip boundary conditions on the bottom, left and right walls. Free-slip boundary conditions are imposed on the top one. Thus free and no slip fronts may be considered in the same simulation.
We do not consider the reduced gravity for the definitions for the dimensionless parameters and set the Reynolds number as 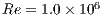 and the Grashof is set to
and the Grashof is set to 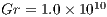 . For this simulation, we disregard the diffusion term of the transport equation (3). So, the Peclet number does not need to be defined. We set the exponent of the nonlinear diffusion operator (19) as
. For this simulation, we disregard the diffusion term of the transport equation (3). So, the Peclet number does not need to be defined. We set the exponent of the nonlinear diffusion operator (19) as 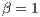 and the time step is set to
and the time step is set to 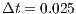 .
.
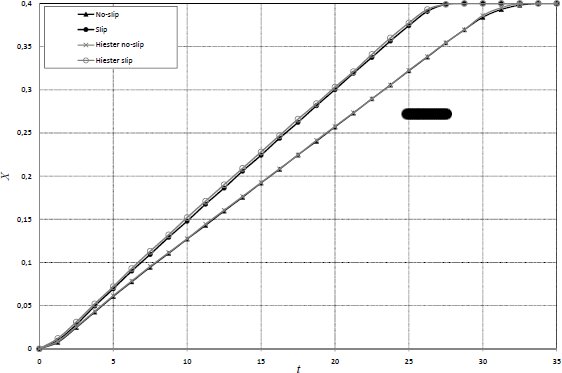
We compare the results from the present adaptive simulation with those obtained using fixed structured mesh with characteristic length 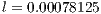 (given by the hexahedron edge). The dimensionless distance of the front head between the two fluids
(given by the hexahedron edge). The dimensionless distance of the front head between the two fluids 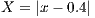 is tracked over time
is tracked over time 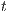 . The distance from the initial position (
. The distance from the initial position (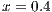 ) of both fronts using the fixed mesh is plotted in Fig. (8)
) of both fronts using the fixed mesh is plotted in Fig. (8)
As expected, free-slip front (top) reaches the vertical wall before the no-slip (bottom) does. Figure (8) shows a good agreement between our results and those obtained by the reference (10). The results from (10) were obtained using a fixed 2D mesh formed by triangles which characteristic length is 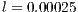 .
.
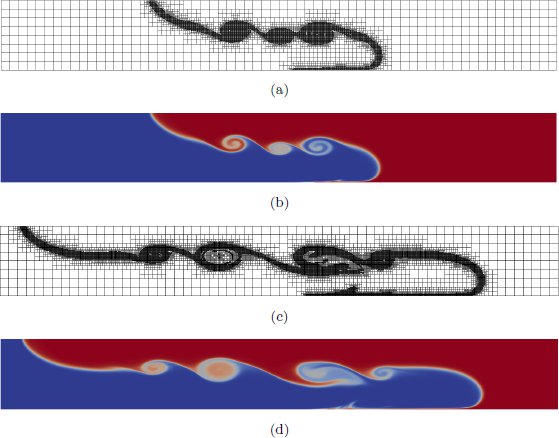
The Fig. (9) shows the temperature distributions and the meshes at two different times with AMR/C at every 10 time-steps. The refinement fraction is set as 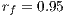 and the coarsening fraction is
and the coarsening fraction is 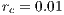 . In order to prevent the size of the elements become too small, we allowed only 4 refinement-levels. The Kelvin-Helmholtz billows are captured by the mesh as the front evolves after the release.
. In order to prevent the size of the elements become too small, we allowed only 4 refinement-levels. The Kelvin-Helmholtz billows are captured by the mesh as the front evolves after the release.
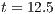 , (b) Temperature distribution at
, (b) Temperature distribution at 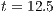 , (c) Adaptive mesh at
, (c) Adaptive mesh at 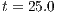 and (d) Temperature distribution at
and (d) Temperature distribution at 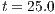
Through the mesh adaptivity simulation, the largest number of elements reached is approximately 30,000. If a fixed structured mesh had been used, to achieve the same refinement level, it would take approximately 131,000 hexaedrons. Therefore, with mesh adaptation we can, in this problem, compute a solution with one order of magnitude less elements without compromising the solution accuracy.
The libMesh framework was used to implement the stabilized SUPG/PSPG finite element formulation for the parallel adaptive solution of incompressible viscous flow and advective-diffusive transport using a trilinear hexahedral element. Good numerical results were obtained for parallel executions with adaptive meshes. AMR/C allows the representation of multiple flow scales and improves resolution where needed. It was possible to track the Kelvin-Helmholtz billows present in the temperature-driven gravity current problem.
This work is partially supported by CNPq and ANP. We are also indebted to Engineering Simulation and Scientific Software (ESSS) to their partial support to A. Rossa in his PhD studies at COPPE/UFRJ. Computer time for the simulations in this work was provided by the High Performance Computing Center at COPPE/UFRJ.
(1) J. Dongarra, I. Foster, G. Fox, W. Gropp, K. Kennedy, L. Torczon, and A. White, Sourcebook of Parallel Computing. San Francisco, CA, USA: Morgan Kaufmann Publishers, 2003.
(2) B. S. Kirk, J. W. Peterson, R. H. Stogner, and G. F. Carey, “libMesh: A C++ Library for Parallel Adaptive Mesh Refinement/Coarsening Simulations,” Engineering with Computers, vol. 22, no. 3–4, pp. 237–254, Nov. 2006, http://dx.doi.org/10.1007/s00366-006-0049-3.
(3) M. Griebel, T. Dornseifer, and T. Neuhoeffer, Numerical Simulation in Fluid Dynamics: A Practical Introduction. Philadelphia, PA, USA: SIAM, 1997.
(4) C. Härtel, E. Meiburg, and F. Necker, “Analysis and direct numerical simulation of the flow at a gravity-current head. Part 1. Flow topology and front speed for slip and no-slip boundaries,” Journal of Fluid Mechanics, vol. 418, pp. 189–212, Apr. 2000.
(5) T. Tezduyar, “Stabilized finite element formulations for incompressible flow computations,” ser. Advances in Applied Mechanics, J. W. Hutchinson and T. Y. Wu, Eds. Elsevier, 1991, vol. 28, pp. 1 – 44. (Online). Available: http://www.sciencedirect.com/science/article/pii/S0065215608701534
(6) Y. Bazilevs, V. Calo, T. Tezduyar, and T. Hughes, “YZβ discontinuity capturing for advection-dominated processes with application to arterial drug delivery,” International Journal for Numerical Methods in Fluids, vol. 54, pp. 593–608, 2007.
(7) R. E. Bank and B. D. Welfert, “A posteriori error estimates for the Stokes problem,” Journal on Numerical Analysis, vol. 28, pp. 591–623, Jun. 1991.
(8) M. Ainsworth and J. Oden, A Posteriori Error Estimation in Finite Element Analysis, ser. Pure and Applied Mathematics. Wiley, 2000. (Online). Available: http://books.google.com.br/books?id=\_HligpOKcjoC
(9) G. Carey, Computational Grids: Generations, Adaptation & Solution Strategies, ser. Series in Computational and Physical Processes in Mechanics and Thermal sciEnces. Taylor & Francis, 1997. (Online). Available: http://books.google.com.br/books?id=0w4iXh4FXKYC
(10) H. Hiester, M. Piggott, and P. Allison, “The impact of mesh adaptivity on the gravity current front speed in a two-dimensional lock-exchange,” Ocean Modelling, vol. 38, no. 1 - 2, pp. 1 – 21, Jan. 2011. (Online). Available: http://www.sciencedirect.com/science/article/pii/S1463500311000060
(11) D. W. Kelly, J. P. De S. R. Gago, O. C. Zienkiewicz, and I. Babuska, “A posteriori error analysis and adaptive processes in the finite element method: Part I - Error analysis,” International Journal for Numerical Methods in Engineering, vol. 19, no. 11, pp. 1593–1619, Nov. 1983. (Online). Available: http://dx.doi.org/10.1002/nme.1620191103
(12) W. Liu and A. Sherman, “Comparative analysis of the Cuthill-McKee and the reverse Cuthill-McKee ordering algorithms for sparse matrices,” Journal on Numerical Analysis, vol. 13, no. 2, pp. 198–213, Apr. 1976.
(13) J. Camata, A. Rossa, A. Valli, L. Catabriga, G. Carey, and A. Coutinho, “Reordering and incomplete preconditioning in serial and parallel adaptive mesh refinement and coarsening flow solutions,” International Journal for Numerical Methods in Fluids, vol. 69, no. 4, pp. 802–823, Jun. 2012. (Online). Available: http://dx.doi.org/10.1002/fld.2614
(14) M. Benzi, “Preconditioning techniques for large linear systems: A survey,” Journal of Computational Physics, vol. 182, no. 2, pp. 418–477, Nov. 2002. (Online). Available: http://www.sciencedirect.com/science/article/pii/S0021999102971767