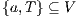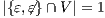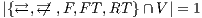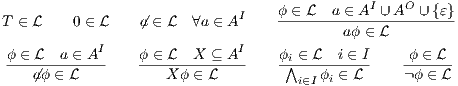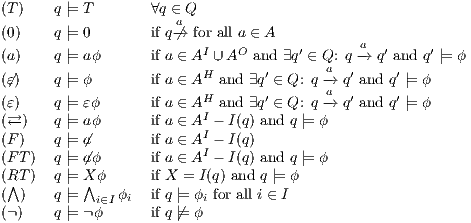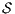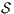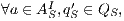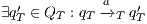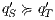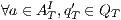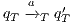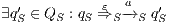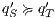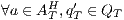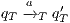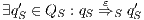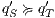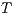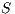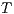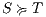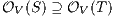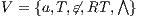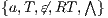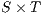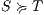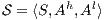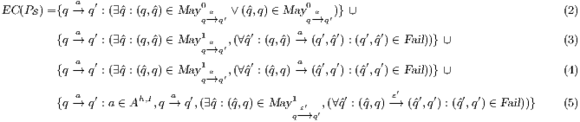Servicios Personalizados
Revista
Articulo
Links relacionados
Compartir
CLEI Electronic Journal
versión On-line ISSN 0717-5000
CLEIej vol.14 no.3 Montevideo dic. 2011
Abstract
An interactive system is a system that allows communication with the users. This communication is modeled through input and output actions. Input actions are controllable by a user of the system, while output actions are controllable by the system. Standard semantics for sequential system [1, 2] are not suitable in this context because they do not distinguish between the different kinds of actions. Applying a similar approach to the one used in [2] we define semantics for interactive systems. In this setting, a particular semantic is associated with a notion of observability. These notions of observability are used as parameters of a general definition of non-interference. We show that some previous versions of the non-interference property based on traces semantic, weak bisimulation and refinement, are actually instances of the observability-based non-interference property presented here. Moreover, this allows us to show some results in a general way and to provide a better understanding of the security properties.
Un sistema interactivo es un sistema que permite comunicación con los usuarios. Esta comunicación es modelada a través de acciones de entrada y de salida. Las acciones de entrada son controladas por un usuario del sistema, mientras las acciones de salida son controladas por el sistema. Las semánticas estándares para sistemas secuenciales [1, 2], no se adaptan bien para este contexto porque éstas no distinguen entre estos tipos de acciones. Aplicando un enfoque similar al utilizado en [2] definimos semánticas para sistemas interactivos. En este contexto, una semántica particular está asociada a una ”noción de observabilidad”. Estas nociones de observabilidad son usadas como parámetro para una definición general de no interferencia. En este trabajo demostramos que versiones anteriores de la propiedad de no-interferencia, basadas en semácticas de trazas, bisimulación débil y refinamiento, son en realidad instancias de la propiedad de no-interferencia basada en nociones de observabilidad presentada en este trabajo. Más aún, este nuevo enfoque permite demostrar algunos resultados en forma general y permite un mejor entendimiento de las propiedades de seguridad.
Keywords: process theory, semantic, interactive systems, interface automata, non interference, secure information flow, refinement, composition.
Teoría de procesos, semántica, sistemas interactivos, autómata de interfaz, no-interferencia, flujos de información seguros, refinamiento, composición
Received: 2011-03-30 Revised: 2011-10-06 Accepted: 2011-10-06
An interactive system is a system that allows communication with the users. Usually, to carry out this communication, the system provides an interface that is used by them. Through the interface, the user sends messages to the system and receives messages from it. Interface Automata (IA) [3, 4, 5] is a light-weight formalism that captures the temporal aspects of interactive system interfaces. In this formalism, the messages sent by the user are represented as input actions, while the received messages are represented as output actions.
Interface structure for security (ISS) [6] is a variant of IA, where there are two different types of visible actions. One type carries public or low confidential information and the other carries private or high confidential information. For simplicity, we call them low and high actions, respectively. Low actions are intended to be accessed by any user while high actions can only be accessed by those users having the appropriate clearance. In this context the desired requirement is the so-called non-interference property [7]. In the setting of ISS, bisimulation based notion of non-interference has been considered, more precisely, the so called BSNNI and BNNI properties [8]. Informally, these properties state that users with no appropriate permission cannot deduce any kind of confidential information or activity by only interacting through low actions. Since it is expected that a low-level user cannot distinguish the occurrence of high actions, the system has to behave the same when high actions are not performed or when high actions are considered as hidden actions. To formalize the idea of “behave the same”, the concept of weak bisimulation is used.
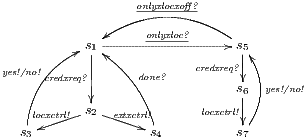
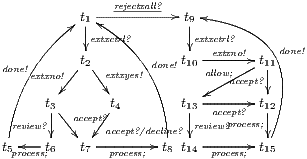
In [9] it was argued that the BSNNI/BNNI properties are not quite appropriate to formalize the concept of secure interface. To illustrate this point the following two examples are presented: in the first one (Figure 1), we get that the system does not satisfy neither BNNI nor BSNNI but we show that it could be considered secure since no information is actually revealed to low users. The main problem is the way in which weak bisimulation relates output transitions. On the other hand, the second example (Figure 2) shows that weak bisimulation based security properties may fail to detect an information leakage through input transitions.
Figure 1 models a credit approval process of an on-line banking service using an ISS. As usual, outputs are suffixed by ! and inputs by ?. At the initial state  , a client can request a credit (cred_req?). The credit approval process can be carried on locally or by delegating it to an external component. This decision is modeled by a non deterministic choice. If it is locally processed (loc_ctrl!), an affirmative or negative response is given to the client (yes!/no!) and the process returns to the initial state. On the other hand, if the decision is delegated (ext_ctrl!), the process waits until it receives a notification that the control is finished (done?), returning then to the initial state. Besides, in the initial state, an administrator can configure the system to do only local control (only_loc?). This action is high and is not visible for low users. (We underline private/high actions.) In state
, a client can request a credit (cred_req?). The credit approval process can be carried on locally or by delegating it to an external component. This decision is modeled by a non deterministic choice. If it is locally processed (loc_ctrl!), an affirmative or negative response is given to the client (yes!/no!) and the process returns to the initial state. On the other hand, if the decision is delegated (ext_ctrl!), the process waits until it receives a notification that the control is finished (done?), returning then to the initial state. Besides, in the initial state, an administrator can configure the system to do only local control (only_loc?). This action is high and is not visible for low users. (We underline private/high actions.) In state  , the administrator can configure the system to return to the original configuration using action only_loc_off?.
, the administrator can configure the system to return to the original configuration using action only_loc_off?.
The Credit Request does not satisfy the BSNNI property (nor the BNNI property) and hence it is considered insecure in this setting. The system behaves differently depending on whether the private action only_loc? is performed or not. If only_loc? is not executed, after action cred_req?, it is possible to execute action ext_ctrl!. This behavior is not possible after the action only_loc?. Notice nevertheless that output actions are not visible for the user until they are executed. Then, from a low user perspective, the system behavior does not seem to change: the same input is accepted at states 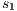 and
and 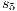 , and then, the low user cannot distinguish whether the observation of loc_ctrl! is a consequence of the unique option (at state
, and then, the low user cannot distinguish whether the observation of loc_ctrl! is a consequence of the unique option (at state 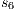 ) or it is just an invariable decision of the Credit Request Process (at state
) or it is just an invariable decision of the Credit Request Process (at state 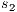 ). Hence we expect the system to be classified as secure by the formalism.
). Hence we expect the system to be classified as secure by the formalism.
We consider this example to be secure because a user does not know exactly what output action can be executed by an interface if he has no knowledge of the current state, he can observe the output actions only when they are executed.
On the other hand, a user may try to guess the behavior of the system by performing input actions: wrong inputs will be rejected/ignored; otherwise, they will be accepted. Based on this fact, the following example shows that weak bisimulation based non-interference may fail to detect an information leakage.
Figure 2 depicts the component that executes the external control. In the initial state, the interface waits for input ext_ctrl? from the Credit Request Process. After this stimulus, a response about the credit request is given. If the credit is denied (ext_no!), the client can either ask for a decision review (review?) or accept the decision (accept?). In both cases, the decision is processed by the component (process;). This action is internal and is not visible by users (hidden/internal action are suffixed by semicolon). The process finishes with action done! returning to the initial state. If the credit is approved (ext_yes!), the client can accept or decline the credit (accept?/decline?). The decision is processed, the component informs that the task is done and it returns to the initial state. As in the first example, the behavior of the component can be modified by an administrator, which can configure the interface to reject all credit requests (reject_all?). For this reason, if reject_all? is received at the initial state, after an input action ext_ctrl?, the process can only execute action ext_no!. At this point, clients are not allowed to ask for a decision review. Then, at state 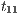 , the interface accepts only input action accept?. However, based on the client records, the review may be enabled; this is represented with the internal transition
, the interface accepts only input action accept?. However, based on the client records, the review may be enabled; this is represented with the internal transition 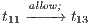 , notice state
, notice state 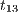 accepts both inputs actions accept? and review?. In any case, after the client response, the result is processed, the component informs that the task is done, and the process is restarted.
accepts both inputs actions accept? and review?. In any case, after the client response, the result is processed, the component informs that the task is done, and the process is restarted.
Suppose that the bank requires that the client cannot detect whether the external process is denying all credit request. Since a low user cannot see the output action until they are executed, he cannot differentiate between the executions 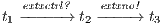 and
and 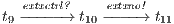 . If we compare states
. If we compare states  and
and  under weak bisimulation, both state can execute the same visible transitions and no security problem is detected. Notice that at state
under weak bisimulation, both state can execute the same visible transitions and no security problem is detected. Notice that at state  , the process cannot respond immediately to a review? input, but it can execute
, the process cannot respond immediately to a review? input, but it can execute 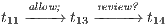 (recall allow; is an internal action). In fact, low users can distinguish state
(recall allow; is an internal action). In fact, low users can distinguish state 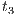 from
from 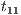 : testing the interface at state
: testing the interface at state 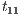 , the low user can find out that input action review? is not enabled, while at
, the low user can find out that input action review? is not enabled, while at 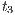 it is. Hence, we consider that the interface is not secure.
it is. Hence, we consider that the interface is not secure.
These observations are based on the fact that input and output actions are conceptually very different. Input actions are controllable by the user while output actions are controllable by the system. Therefore, some behavior one would expect from input actions may be inappropriate for outputs and vice-versa. For instance, the assumption that “wrong inputs will be rejected/ignored; otherwise, they will be accepted” in the second example above, makes no sense if applied to outputs because the malicious user is interested in collecting all possible information rather than in rejecting it.
In [1] and [2], a deep study about semantic for sequential system is done, but they do not take in account systems where both kinds of actions coexist. In their setting all actions are controlled by one entity: the user or the system. For example, in Fail Trace Semantic a user executes (input) actions until one action is rejected by the system, in this case the user has the control of which action is executed. A different case is Trace Semantic where the system has the control of the actions and the user can only observe the executions of the system. Also in stronger semantics, for example with global testing, the control belongs to one entity. For instance, Weak Bisimulation equivalence is also called observational equivalence and its intuitive notion is “two system are observational equivalence if they cannot be distinguished by an observer”, ie the user observes and the system executes (controls) the actions. Notice the subtlety in this case: global testing allows the user to force the system to execute all possible executions but, which actions can be executed in each state is controlled/defined by the system.
In this work we define semantics for systems where both coexist, actions controlled by the user (input actions) and actions controlled by the system (output actions). We have used an approach similar to the one used in [2]. First we define types of observations, an information record that can be performed by a user. Second, we define a notion of observability as a set of types of observations. Each notion of observability is a particular semantic. This approach is simple, elegant and allows to be exhaustive: when the types of observation and notion of observability are defined one has all the possible semantics that could be defined.
These new semantics are suitable to study secure information flow properties over ISS. Moreover, the definition of non-interference presented in this work has as parameter a notion of observability. This generalization through types of observations provides a framework to prove generic theorems that extends to families of security properties. In addition, the approach subsumes previous definitions of non-interference for ISS, in particular the one based on traces [9], the one based on weak bisimulation [6] and the one based on refinement [9].
We also focus our attention in non-interference based on refinement. We give sufficient and simple conditions to ensure compositionality. We also provide two algorithms. The first one determines if an ISS satisfies the refinement-based non-interference property. The second one, determines if an ISS can be made secure by controlling some input actions, and if so, synthesizes the secure ISS. Both algorithms are polynomial in the number of states of the ISS under study. These results are relevant because they could be adapted to other instances of non interference based on notion of observability.
This paper is an extension of [9]. In [9] we introduce non-interference based on refinement to resolve some shortcomings in the non-interference based on weak bisimulation properties. The approach based on notions of observability shows that the shortcomings do not exist because the properties should be considered in different contexts. We explain this in the last section of the paper.
Organization of the paper. In section 2 we recall definitions of IA, composition and ISS. In section 3 we define the types of observations, notion of observability and the set of observable behaviors of an IA. In section 4 we present the notion of non-interference based on notion of observability. We show that the approach subsumes previous definition of non-interference for ISS and we proof some general properties of non-interference. In section 5 we review the definitions of non-interference based on refinement, and we show that these definitions also are subsumed by the new approach. We study compositionality in this setting and define two algorithms: one to check whether an interface satisfies the property and the another to derive a secure interface from a given (non-secure) interface by controlling inputs actions. Section 6 concludes the paper.
2 Interfaces Automata and Interface Structure for Security
In the following, we define Interface Automata (IA) [3, 4] and Interface Structure for Security (ISS) [6], and introduce some notations.
Definition 1. An Interface Automaton (IA) is a tuple 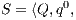
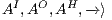 where: (i)
where: (i) 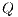 is a finite set of states with
is a finite set of states with 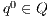 being the initial state; (ii)
being the initial state; (ii) 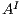 ,
, 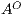 , and
, and 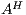 are the (pairwise disjoint) finite sets of input, output, and hidden actions, respectively, with
are the (pairwise disjoint) finite sets of input, output, and hidden actions, respectively, with 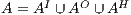 ; and (iii)
; and (iii)  is the transition relation that is required to be finite and input deterministic (i.e.
is the transition relation that is required to be finite and input deterministic (i.e. 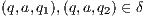 implies
implies 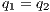 for all
for all 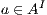 and
and 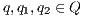 ). In general, we denote
). In general, we denote 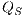 ,
, 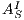 ,
, 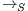 , etc. to indicate that they are the set of states, input actions, transitions, etc. of the IA
, etc. to indicate that they are the set of states, input actions, transitions, etc. of the IA 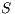 .
.
As usual, we denote 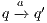 whenever
whenever 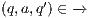 ,
, 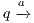 if there is
if there is 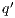 s.t.
s.t. 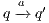 , and
, and 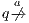 if this is not the case. An execution of
if this is not the case. An execution of  is a finite sequence
is a finite sequence 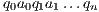 s.t.
s.t. 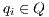 ,
, 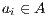 and
and 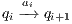 for
for 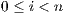 . An execution is autonomous if all their actions are output or hidden (the execution does not need stimulus from the environment to run). If there is an autonomous execution from
. An execution is autonomous if all their actions are output or hidden (the execution does not need stimulus from the environment to run). If there is an autonomous execution from 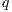 to
to 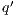 and all action are hidden, we write
and all action are hidden, we write 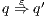 . Notice this includes case
. Notice this includes case 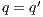 . We write
. We write 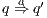 if there are
if there are 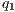 and
and 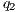 s.t.
s.t. 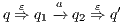 . Moreover
. Moreover 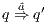 denotes
denotes 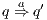 or
or 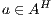 and
and 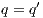 . We write
. We write 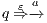 if there is
if there is 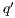 s.t.
s.t. 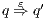 and
and 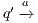 . A trace from
. A trace from 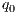 is a sequence of visible actions
is a sequence of visible actions 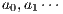 such that there are states
such that there are states 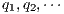 such that
such that 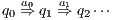 is an execution. The set of traces of an IA
is an execution. The set of traces of an IA 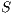 , notation
, notation 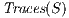 , is the set of all traces from the initial state of
, is the set of all traces from the initial state of 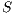 .
.
Composition of two IA is only defined if their actions are disjoint except when input actions of one of the IA coincide with some of the output actions of the other. Such actions are intended to synchronize in a communication.
Definition 2. Let 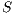 and
and 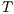 be two IA, and let
be two IA, and let 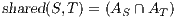 be the set of shared actions. We say that
be the set of shared actions. We say that 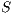 and
and 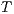 are composable whenever
are composable whenever 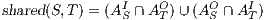 . Two ISS
. Two ISS 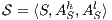 and
and 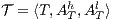 are composable if
are composable if 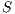 and
and 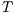 are composable.
are composable.
The product of two composable IA  and
and  is defined pretty much as CSP parallel composition: (i) the state space of the product is the product of the set of states of the components, (ii) only shared actions can synchronize, i.e., both component should perform a transition with the same synchronizing label (one input, and the other output), and (iii) transitions with non-shared actions are interleaved. Besides, shared actions are hidden in the product.
is defined pretty much as CSP parallel composition: (i) the state space of the product is the product of the set of states of the components, (ii) only shared actions can synchronize, i.e., both component should perform a transition with the same synchronizing label (one input, and the other output), and (iii) transitions with non-shared actions are interleaved. Besides, shared actions are hidden in the product.
Definition 3. Let 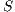 and
and 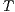 be composable IA. The product
be composable IA. The product 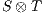 is the interface automaton defined by:
is the interface automaton defined by:
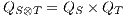 with
with 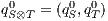 ;
; 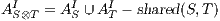 ,
, 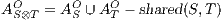 , and
, and 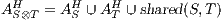 ; and
; and 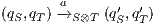 if any of the following holds:
if any of the following holds: 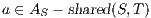 ,
, 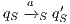 , and
, and 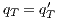 ;
; 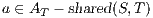 ,
, 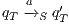 , and
, and 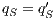 ;
; 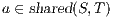 ,
, 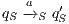 , and
, and 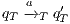 .
.
There may be reachable states on 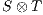 for which one of the components, say
for which one of the components, say 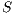 , may produce an output shared action that the other is not ready to accept (i.e., its corresponding input is not available at the current state). Then
, may produce an output shared action that the other is not ready to accept (i.e., its corresponding input is not available at the current state). Then 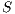 violates the input assumption of
violates the input assumption of 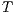 and this is not acceptable. States like these are called error states.
and this is not acceptable. States like these are called error states.
Definition 4. Let 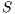 and
and 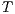 be composable IA. A product state
be composable IA. A product state 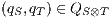 is an error state if there is an action
is an error state if there is an action 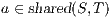 s.t. either
s.t. either  ,
, 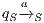 and
and 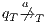 , or
, or 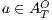 ,
, 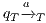 and
and 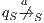 .
.
If the product 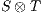 does not contain any reachable error state, then each component satisfies the interface of the other (i.e., the input assumptions) and thus are compatible. Instead, the presence of a reachable error state is evidence that one component is violating the interface of the other. This may not be a major problem as long as the environment is able to restrain of producing an output (an input to
does not contain any reachable error state, then each component satisfies the interface of the other (i.e., the input assumptions) and thus are compatible. Instead, the presence of a reachable error state is evidence that one component is violating the interface of the other. This may not be a major problem as long as the environment is able to restrain of producing an output (an input to 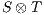 ) that leads the product to the error state. Of course, it may be the case that
) that leads the product to the error state. Of course, it may be the case that 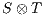 does not provide any possible input to the environment and reaches autonomously (i.e., via output or hidden actions) an error state. In such a case we say that
does not provide any possible input to the environment and reaches autonomously (i.e., via output or hidden actions) an error state. In such a case we say that 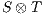 is incompatible.
is incompatible.
Definition 5. Let 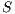 and
and 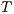 be composable IA and let
be composable IA and let 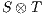 be its product. A state
be its product. A state 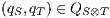 is an incompatible state if there is an error state reachable from
is an incompatible state if there is an error state reachable from 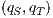 through an autonomous execution. If a state is not incompatible, it is compatible. If the initial state of
through an autonomous execution. If a state is not incompatible, it is compatible. If the initial state of 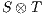 is compatible, then
is compatible, then  and
and  are compatible.
are compatible.
Finally, if two IA are compatible, it is possible to define the interface for the resulting composition. Such interface is the result of pruning all input transitions of the product that lead to incompatible states i.e. states from which an error state can be autonomously reached.
Definition 6. Let 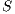 and
and 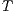 be compatible IA. The composition
be compatible IA. The composition 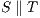 is the IA that results from
is the IA that results from 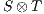 by removing all transition
by removing all transition 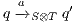 s.t. (i)
s.t. (i) 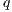 is a compatible state in
is a compatible state in 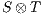 , (ii)
, (ii) 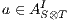 , and (iii)
, and (iii) 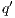 is an incompatible state in
is an incompatible state in  .
.
2.2 Interface Structure For Security
An Interface Structures for Security is an IA, where visible actions are divided in two disjoint sets: the high action set and the low action set. Low actions can be observed and used for any user, while high actions are intended only for users with the appropriate clearance.
Definition 7. An Interface Structure for Security (ISS) is a tuple 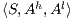 where
where 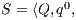
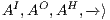 is an IA and
is an IA and 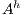 and
and 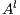 are disjoint sets of actions s.t.
are disjoint sets of actions s.t. 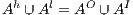 .
.
If necessary, we will write 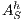 and
and 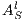 instead of
instead of 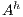 and
and 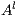 , respectively, and write
, respectively, and write 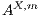 instead of
instead of 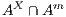 with
with 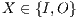 and
and 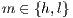 .
.
Extending the definition of composition of IA to ISS is straightforward.
Definition 8. Let 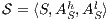 and
and 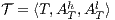 be two ISS.
be two ISS. 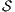 and
and 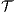 are composable if
are composable if 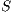 and
and 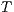 are composable. Given two composable ISS,
are composable. Given two composable ISS, 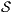 and
and 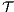 , their composition,
, their composition, 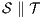 , is defined by the ISS
, is defined by the ISS 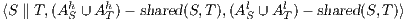 .
.
Semantic equivalences for sequential systems with silent moves are studied in [2]. Resulting in 155 notions of observability and a complete comparison between them. Unfortunately, these results cannot be applied straightforward to the IA context. For example, studied machines in [2] have not notions of input and output actions over the same machine. Moreover, in [2] there is not a notion of the internal structure of the analyzed machine. This situation have forced them to talk about definite and hypothetical behaviors of the machine. Despite these differences, we use [2] as a reference to define different semantics for IA. To avoid the distinction between definite and hypothetical behaviors, we use the transition relation of the IA to present the set of observable behaviors.
First we define type of observation, an information record that can be done by the user. Second, we define a notion of observability as a set of types of observations. Each notion of observability defines a particular semantic. Third, using the transition relation of the IA, we define the semantic of each type of observation and therefore a semantic for each possible notion of observability.
Given a system, a type of observation is an information that can be recorded by a user with respect to the interface. To define our types of observations we consider the following assumptions: input and output actions are observable when they are executed. Inputs are executed by a user, while outputs are executed by the interface. Then, input actions are controllable by the user and output actions are controllable by the interface. Internal transitions are controllable by the interface. In some cases, internal transitions can be detectable by the user but the user cannot distinguish between different internal actions. An user can observe how the interface interact with another user or he can be the one who interacts. If the user is interacting, the interface can behave in different ways as a result of some violation of its input assumptions: (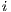 ) it does not show any error and continues with the execution, (
) it does not show any error and continues with the execution, (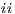 ) it stops the execution and shows an error to the user, (
) it stops the execution and shows an error to the user, ( ) it shows an error to the user and continues with the execution; (
) it shows an error to the user and continues with the execution; ( ) finally, an interface could provide a special service to inform which inputs are enabled in its current state. In this way, the user can avoid input assumption violations. Notice that cases (
) finally, an interface could provide a special service to inform which inputs are enabled in its current state. In this way, the user can avoid input assumption violations. Notice that cases ( ), (
), ( ) and (
) and ( ) determine, at the semantic level, a sort of input-enableness. In these cases we fix the behavior of input actions that are not defined in a particular state. The last four assumptions do not increase the expressiveness power of the model, as consequence they can be implemented in any IA. For example: let
) determine, at the semantic level, a sort of input-enableness. In these cases we fix the behavior of input actions that are not defined in a particular state. The last four assumptions do not increase the expressiveness power of the model, as consequence they can be implemented in any IA. For example: let  be an IA, the assumption
be an IA, the assumption 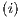 can be implemented with self loops with action
can be implemented with self loops with action 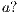 for all state state
for all state state 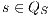 and
and 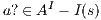 . Using the same reasoning, we assume an interface could provide a service to detect the end of an execution, where the end is reached when no more transitions are possible. In addition, a user can make copies of the interface with the objective of studying the interface in more detail. Finally, a user can do global testing. Under this assumption it is possible to say that a particular observation will not happen.
. Using the same reasoning, we assume an interface could provide a service to detect the end of an execution, where the end is reached when no more transitions are possible. In addition, a user can make copies of the interface with the objective of studying the interface in more detail. Finally, a user can do global testing. Under this assumption it is possible to say that a particular observation will not happen.
Based on these assumptions, we introduce the following types of observations:
- [
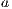 ] The execution of external actions
] The execution of external actions 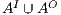 are detectable.
are detectable. - [
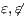 ] The case of internal transitions are detectable is denoted with
] The case of internal transitions are detectable is denoted with 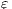 . Otherwise
. Otherwise 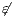 .
. - [
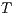 ] The session is terminated by the user. This is possible in any time. After this no more records are possible
] The session is terminated by the user. This is possible in any time. After this no more records are possible - [
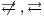 ] If a user only observes the actions that are executed by an interface and cannot send stimuli to it, then there is no interaction. We denote this with
] If a user only observes the actions that are executed by an interface and cannot send stimuli to it, then there is no interaction. We denote this with 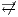 . The case where the interaction is possible is denoted by
. The case where the interaction is possible is denoted by 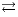 .
. - [
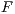 ] The user interacts with system and the interface stops the execution whenever it receives an input action that is not enabled. In this case, the stop is observable.
] The user interacts with system and the interface stops the execution whenever it receives an input action that is not enabled. In this case, the stop is observable. - [
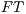 ] Suppose the previous type but now whenever the interface receives an input action that is not enabled, the error is informed to the user and the execution continues.
] Suppose the previous type but now whenever the interface receives an input action that is not enabled, the error is informed to the user and the execution continues. - [
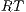 ] To avoid the error of sending an input action that is not enabled, the interface can provide a method to check what input actions are enabled in its current state. In this case, the observation includes the set
] To avoid the error of sending an input action that is not enabled, the interface can provide a method to check what input actions are enabled in its current state. In this case, the observation includes the set 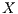 of enabled inputs.
of enabled inputs. - [
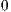 ] This type is used if it is detectable when an interface reachs a final state, i.e. no more activity is possible.
] This type is used if it is detectable when an interface reachs a final state, i.e. no more activity is possible. - [
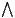 ] Suppose the user has a machine to make arbitrary number of copies of the system. These copies reveal more information about the interface because one could observes different execution from the same interface. If the user makes
] Suppose the user has a machine to make arbitrary number of copies of the system. These copies reveal more information about the interface because one could observes different execution from the same interface. If the user makes 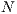 copies and in each copy executes
copies and in each copy executes 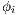 for
for 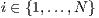 , this observations is denoted with
, this observations is denoted with 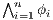 .
. - [
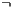 ] It is possible to test the interface over all possible condition. This allows to ensure that a particular observation is not possible; then a user can do an observation
] It is possible to test the interface over all possible condition. This allows to ensure that a particular observation is not possible; then a user can do an observation 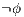 whenever
whenever 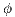 is not possible execution of the system.
is not possible execution of the system.
The types of observations studied here are not the studies in [2]. On one hand, we decided to skip some types for the sake of simplicity. For example we did not include 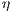 -replication nor continuous copying, which are different forms of make copies of the system. We did not include the notion of stable state, this avoids the inclusion of some variant of types of visibilities presented here. On the other hand, we have added new features. First, we differentiate between a user that interacts with the interface and a non-interacting user. Second, the knowledge of the internal structure of the interface allow us to know exactly when an internal action could be executed and define if the internal transitions are observable or not. This is a relevant feature in the context of security, because it could be used to represent covert channels.
-replication nor continuous copying, which are different forms of make copies of the system. We did not include the notion of stable state, this avoids the inclusion of some variant of types of visibilities presented here. On the other hand, we have added new features. First, we differentiate between a user that interacts with the interface and a non-interacting user. Second, the knowledge of the internal structure of the interface allow us to know exactly when an internal action could be executed and define if the internal transitions are observable or not. This is a relevant feature in the context of security, because it could be used to represent covert channels.
A set of types of observations defines a notion of observability, see Definition 9. The notion of observability determines what information can be observed by a user. This has to be consistent, for example, types of observations “a user cannot interact with the interface” (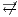 ) and “a user can detect that the input sent was not enabled” (
) and “a user can detect that the input sent was not enabled” (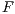 ) cannot belong to same notion of observability. Note that the definition of notion of observability ensures consistency.
) cannot belong to same notion of observability. Note that the definition of notion of observability ensures consistency.
Definition 9. A set 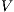 is a notion of observability (for IA) if
is a notion of observability (for IA) if 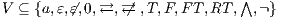 and
and 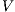 satisfies the following conditions:
satisfies the following conditions:
Condition (1) ensures that input and output actions are always visible and that the user can terminate the session when he wants. Condition (2) ensures that internal transitions are detectable or not. Condition (3) ensures that a user can interact with the interface (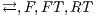 ) or not (
) or not (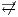 ), and if he interacts, he will do in one particular way.
), and if he interacts, he will do in one particular way.
In [2] other kind of restrictions were added to simplify the study of which semantics make more differences: for example conditions as “if 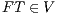 then
then 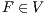 ” are added. This reflects the fact that if the interface stops when a disable input is received, all observations that one can do in this scenario, can be done in the same machine configured to continue when the error occurs. Since we are not interested in studying which semantics is coarser than others, we omit these conditions.
” are added. This reflects the fact that if the interface stops when a disable input is received, all observations that one can do in this scenario, can be done in the same machine configured to continue when the error occurs. Since we are not interested in studying which semantics is coarser than others, we omit these conditions.
Semantic. First we define all possible observations as a set of logic formulas called execution formulas. Then the set of observable behavior of an IA is the set of execution formulas that are satisfied by the initial state of the interface.
Definition 10. The set of execution formulas  for an IA
for an IA 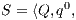
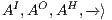 is the smallest set satisfying rules in Table 1.
is the smallest set satisfying rules in Table 1.
Definition 11. Given an IA 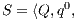
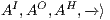 and a notion of observability
and a notion of observability 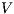 , the satisfaction relation
, the satisfaction relation 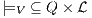 is defined for each type of observation in
is defined for each type of observation in 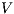 by clauses in Table 2. The observables behavior of an IA
by clauses in Table 2. The observables behavior of an IA 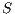 with notion of observability
with notion of observability 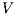 is
is 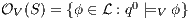
4 Non interference based on Notion of Observability.
First we introduce a general notion of non-interference. Informally, non-interference states that users with no appropriate permission cannot deduce any kind of confidential information or activity by only interacting through low actions. Since it is expected that a low-level user cannot distinguish the occurrence of high actions, the system has to behave the same when high actions are not performed or when high actions are considered as hidden actions. Hence, restriction and hiding are central to our definitions of security.
Definition 12. Given an IA 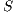 and a set of actions
and a set of actions 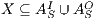 , define:
, define:
- the restriction of
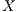 in
in 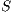 by
by 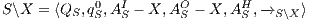 where
where 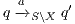 iff
iff 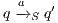 and
and  .
. - the hiding of
 in
in  by
by  .
.
Given an ISS 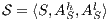 define the restriction of
define the restriction of 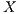 in
in 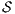 by
by 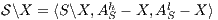 and the hiding of
and the hiding of 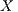 in
in 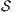 by
by 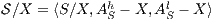 .
.
Definition 13. Let 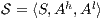 be an ISS and
be an ISS and 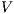 a notion of observability, then:
a notion of observability, then:
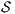 is
is 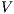 strong non-deterministic non-interference (
strong non-deterministic non-interference (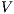 -SNNI) if
-SNNI) if 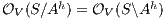 .
. 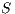 is
is 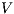 non-deterministic non-interference (
non-deterministic non-interference (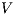 -NNI) if
-NNI) if 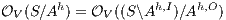 .
.
Notice the difference between the two definitions. 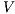 -SNNI formalizes the security property as we described so far: a system satisfies
-SNNI formalizes the security property as we described so far: a system satisfies 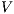 -SNNI if a low-level user cannot distinguish (up to notion of observability
-SNNI if a low-level user cannot distinguish (up to notion of observability 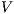 ) by means of low level actions (the only visible ones) whether the system performs high actions (so they are hidden) or not (high actions are restricted). In the definition of
) by means of low level actions (the only visible ones) whether the system performs high actions (so they are hidden) or not (high actions are restricted). In the definition of 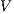 -NNI only high input actions are restricted since the low-level user cannot provide this type of actions; instead high output actions are only hidden since they still can autonomously occur. The second notion is considered as it seems appropriate for IA where only input actions are controllable.
-NNI only high input actions are restricted since the low-level user cannot provide this type of actions; instead high output actions are only hidden since they still can autonomously occur. The second notion is considered as it seems appropriate for IA where only input actions are controllable.
The approach of non-interference based on notion of observability generalizes other notion of non-interference for IA. For example Non deterministic Non-Interference (NNI), Strong Non deterministic Non-Interference (SNNI), both based on trace equivalence; Bisimulation NNI (BNNI) and Bisimulation SNNI (BSNNI) both based on bisimulation equivalence. To prove our statement, we recall the definitions of trace equivalence, weak bisimulation and non-interference properties.
Definition 14. Let 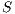 and
and 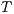 be two IA.
be two IA. 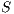 and
and 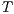 are trace equivalent, notation
are trace equivalent, notation 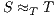 , if
, if 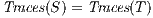 . We say that two ISS
. We say that two ISS 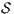 and
and 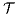 are trace equivalent, and write
are trace equivalent, and write 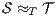 , whenever the underlying IA are trace equivalent.
, whenever the underlying IA are trace equivalent.
Definition 15. Let 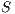 and
and 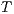 be two IA. A relation
be two IA. A relation 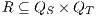 is a (weak) bisimulation between
is a (weak) bisimulation between 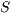 and
and 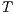 if
if 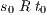 and, for all
and, for all 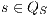 and
and 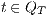 ,
, 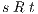 implies:
implies:
- for all
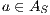 and
and 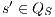 ,
, 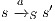 implies that there exists
implies that there exists 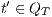 s.t.
s.t. 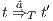 and
and 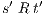 ; and
; and - for all
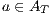 and
and 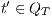 ,
, 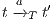 implies that there exists
implies that there exists 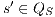 s.t.
s.t. 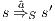 and
and 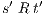 .
.
We say that 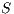 and
and 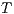 are bisimilar, notation
are bisimilar, notation 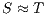 , if there is a bisimulation between
, if there is a bisimulation between 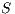 and
and 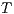 . Moreover, we say that two ISS
. Moreover, we say that two ISS 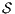 and
and 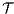 are bisimilar, and write
are bisimilar, and write 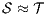 , whenever the underlying IA are bisimilar.
, whenever the underlying IA are bisimilar.
- 1.
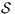 satisfies strong non-deterministic non-interference (SNNI) if
satisfies strong non-deterministic non-interference (SNNI) if 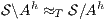 .
. - 2.
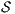 satisfies non-deterministic non-interference (NNI) if
satisfies non-deterministic non-interference (NNI) if 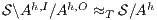 .
. - 3.
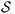 satisfies bisimulation-based strong non-deterministic non-interference (BSNNI) if
satisfies bisimulation-based strong non-deterministic non-interference (BSNNI) if 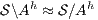 .
. - 4.
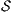 satisfies bisimulation-based non-deterministic non-interference (BNNI) if
satisfies bisimulation-based non-deterministic non-interference (BNNI) if 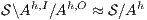 .
.
We prove how to represent these notions of security with notions of observability.
Proof. First we prove (2). For this, we have to show that for all states 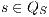 and
and 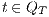 it holds
it holds 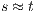 iff
iff 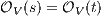 .
.  Suppose
Suppose 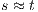 and
and 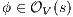 . Let
. Let 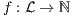 a function defined as:
a function defined as:
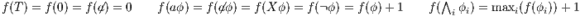 |
We define 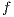 in general for all
in general for all 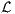 since we will make use of it again later. We proceed by complete induction. In the base case
since we will make use of it again later. We proceed by complete induction. In the base case 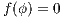 then
then 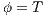 because
because 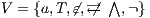 and since
and since 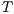 is an observation for every state
is an observation for every state 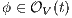 . By induction suppose that if
. By induction suppose that if 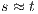 then, if
then, if 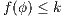 and
and 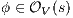 it holds
it holds 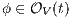 . Let
. Let 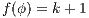 , we do case analysis according to the shape of the formula. Suppose
, we do case analysis according to the shape of the formula. Suppose 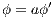 with
with 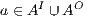 .
. 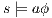 implies
implies 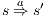 and
and 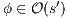 (see
(see  and
and  in Table 2). Since
in Table 2). Since  there is state
there is state 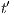 such that
such that 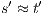 . By induction
. By induction 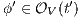 , therefore
, therefore 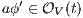 . Now let
. Now let 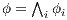 . Since
. Since 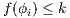 for all
for all 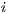 , by induction
, by induction 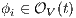 . Therefore
. Therefore 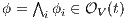 . Now suppose
. Now suppose 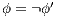 then
then 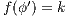 and
and 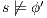 , by induction
, by induction 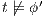 . Therefore
. Therefore 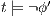 , ie
, ie 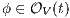 . The other cases are outside of the observation defined by
. The other cases are outside of the observation defined by 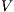 . The symmetric case is analogous.
. The symmetric case is analogous.
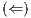 Let
Let 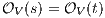 and
and 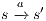 . We have to show that there is
. We have to show that there is 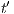 such that
such that 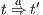 and
and 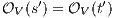 . Since
. Since 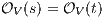 we have
we have 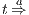 . Let
. Let 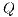 be
be 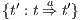 . If for all
. If for all 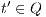 it holds
it holds 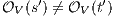 then there is
then there is 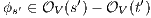 (as consequence of
(as consequence of 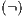 ). Then for any
). Then for any 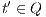 it holds
it holds 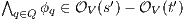 (at least one
(at least one 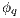 fails). But then
fails). But then 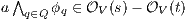 contradicting
contradicting 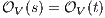 . The symmetric case is analogous.
. The symmetric case is analogous.
To prove (1) we show that given two IA 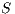 and
and 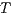 it holds
it holds 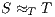 iff
iff 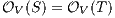 . We reduce this to prove
. We reduce this to prove 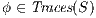 iff
iff 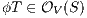 . This proof is straightforward. __
. This proof is straightforward. __
The relation between 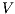 -SNNI and
-SNNI and 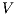 -NNI depends on the notion observability
-NNI depends on the notion observability 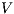 . In general, we only can ensure
. In general, we only can ensure 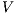 -NNI is not stronger than
-NNI is not stronger than 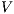 -SNNI for all
-SNNI for all 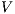 .
.
Proof. Let 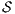 the following ISS
the following ISS 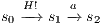 with
with 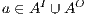 . Notice
. Notice 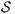 is always
is always 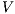 -NNI. On the other hand
-NNI. On the other hand 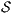 is not
is not 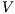 -SNNI: if
-SNNI: if 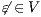 then
then 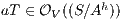 and
and 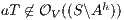 ; if
; if 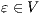 then
then 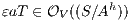 and
and 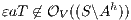 . __
. __
This result is not novel. In [8], it is shown that SNNI is stronger than NNI. Therefore as trace semantic is the coarsest sensible semantic on labeled transition system, it is natural that the result holds for all other semantic. The Theorem 2 only formalize this fact for IA semantics.
The other relations depend on 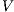 and we state in the following two theorems. Previously an auxiliary lemma.
and we state in the following two theorems. Previously an auxiliary lemma.
Lemma 1. Let 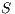 be an IA and
be an IA and 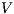 a notion of observability such that
a notion of observability such that 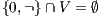 . Let
. Let 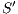 be an IA obtained by removing a set of internal transitions from
be an IA obtained by removing a set of internal transitions from 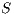 . Then
. Then 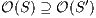 .
.
Proof. The proof is straightforward by induction in 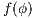 where
where 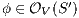 and
and 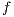 is the function defined in (1). __
is the function defined in (1). __
Proof. If 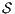 is
is 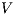 -SNNI then
-SNNI then 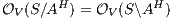 . Notice
. Notice 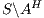 is obtained by removing some hidden transitions from
is obtained by removing some hidden transitions from 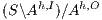 , then
, then 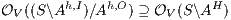 by Lemma 1, and therefore
by Lemma 1, and therefore 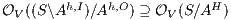 . On the other hand
. On the other hand 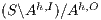 is obtained by removing some hidden transitions from
is obtained by removing some hidden transitions from 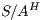 then
then 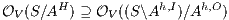 by Lemma 1. Both inclusions imply
by Lemma 1. Both inclusions imply 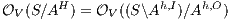 . __
. __
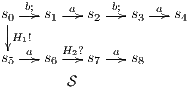
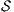 is
is 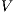 -SNNI does not imply
-SNNI does not imply 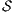 is
is 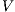 -NNI if
-NNI if 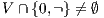
Theorem 4. For all notion of observability 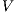 such that
such that 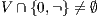 there is an ISS
there is an ISS 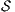 such that
such that 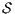 is
is 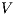 -SNNI and
-SNNI and 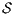 is not
is not 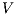 -NNI.
-NNI.
Proof. Define 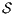 as ISS in Figure 3 with
as ISS in Figure 3 with 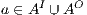 . Clearly
. Clearly 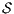 is
is 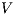 -SNNI for all
-SNNI for all 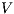 . Suppose
. Suppose 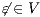 : if
: if 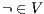 then
then 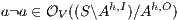 while
while 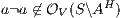 ; if
; if 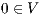 then
then 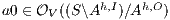 while
while 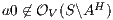 . Then
. Then 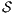 is not
is not 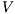 -NNI for any
-NNI for any 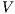 such that
such that 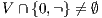 . The case
. The case 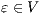 is analogous. __
is analogous. __
The approach based on notion of observability also allows to show that security properties are not preserved by composition.

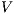 -SNNI and
-SNNI and 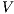 -NNI properties are not preserved by composition.
-NNI properties are not preserved by composition.
Theorem 5. For all notion of observability 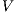 there are ISS
there are ISS 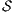 and
and 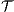 such that
such that 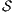 and
and 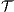 are
are 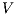 -(S)NNI and composable, and the composition
-(S)NNI and composable, and the composition 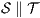 is not
is not 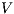 -(S)NNI.
-(S)NNI.
Proof. Let 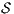 and
and 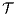 be ISS depicted in Figure 4. Both interfaces are
be ISS depicted in Figure 4. Both interfaces are 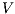 -(S)NNI for all notion of observability
-(S)NNI for all notion of observability 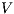 but
but 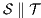 is not. If
is not. If 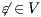 then
then 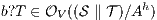 while if
while if 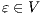 then
then 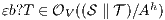 . In any case,
. In any case, 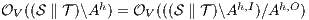 and
and 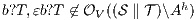 . Then
. Then  is not
is not  -(S)NNI. __
-(S)NNI. __
5 Non-interference based on refinement.
In [9], we presented definitions of non interference based on refinement. The new versions of non-interference were introduced to solve some shortcomings detected in the definitions of non interference based on bisimulation of [6], ie BSNNI and BNNI. In this section we review the results obtained.
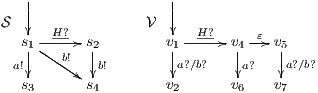
To address the shortcomings detected in B(S)NNI properties, a variation of non-interference based on refinement was introduced. These variants are obtained from the definition of BSNNI and BNNI by replacing weak bisimulation by a new relation. Under this new relation, two states  and
and 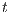 are related if they are able to receive the same input actions; in addition, for every output transition that can execute
are related if they are able to receive the same input actions; in addition, for every output transition that can execute 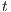 , the state
, the state 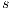 can execute zero or more hidden transitions before executing the same output; finally, all hidden transitions that can execute
can execute zero or more hidden transitions before executing the same output; finally, all hidden transitions that can execute 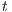 can be “matched” by
can be “matched” by 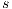 with zero or more hidden transitions. In all cases, the reached states have to be also related. In this way state
with zero or more hidden transitions. In all cases, the reached states have to be also related. In this way state 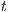 does not reveal new visible behavior w.r.t. the state
does not reveal new visible behavior w.r.t. the state 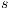 . Formally:
. Formally:
Definition 17. Given two IA 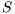 and
and 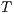 , a relation
, a relation 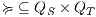 is a Strict Input Refinement (SIR) of
is a Strict Input Refinement (SIR) of  by
by  if
if 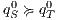 and for all
and for all 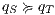 it holds:
it holds:
We say 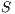 is refined (strictly on inputs) by
is refined (strictly on inputs) by 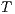 , or,
, or, 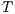 refines (strictly on inputs) to
refines (strictly on inputs) to 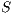 , notation
, notation 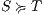 , if there is a SIR
, if there is a SIR 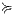 s.t.
s.t. 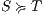 . Let
. Let 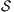 and
and 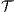 be two ISS, we write
be two ISS, we write 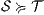 if the underlying IA satisfy
if the underlying IA satisfy 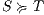 .
.
The definition of SIR is based on the definition of refinement of [5] only that restriction (b) is new with respect to the original version. Based on this relation are defined non-interference properties based on refinement. They are called SIR-NNI and SIR-SNNI.
Definition 18. Let 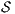 be an ISS. (i)
be an ISS. (i) 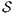 is SIR-based strong non-deterministic non-interference (SIR-SNNI) if
is SIR-based strong non-deterministic non-interference (SIR-SNNI) if 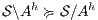 (ii)
(ii) 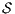 is SIR-based non-deterministic non-interference (SIR-NNI) if
is SIR-based non-deterministic non-interference (SIR-NNI) if 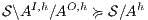 .
.
This new formalization of security ensures that under the presence of high level activity no new information is revealed to low users w.r.t. the system with only low activity, because the interface 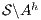 (resp.
(resp. 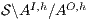 ) is refined by
) is refined by 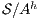 .
.
Now we show there is a notion of observability 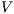 such that
such that 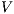 -(S)NNI is equivalent to SIR-(S)NNI. To prove the result we need the following theorem:
-(S)NNI is equivalent to SIR-(S)NNI. To prove the result we need the following theorem:
Proof. For this, we have to show that for all states 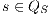 and
and 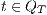 it holds
it holds 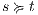 iff
iff 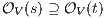 .
.  Suppose
Suppose 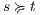 and
and 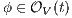 . Let
. Let 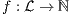 the function defined in (1). We proceed by complete induction. In the base case
the function defined in (1). We proceed by complete induction. In the base case 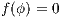 then
then 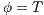 because
because 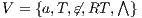 and since
and since 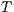 is an observation for every state, then
is an observation for every state, then 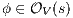 . Inductive case. By induction suppose that if
. Inductive case. By induction suppose that if 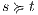 then, if
then, if 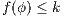 and
and 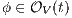 it holds
it holds 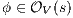 . Let
. Let 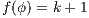 , we do case analysis according to the shape of the formula. Suppose
, we do case analysis according to the shape of the formula. Suppose 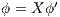 . Since
. Since 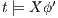 then
then 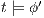 . Moreover,
. Moreover, 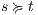 implies
implies 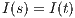 and therefore
and therefore 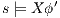 using induction. Cases
using induction. Cases 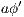 and
and 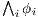 are like this respective case in proof of Theorem 1.
are like this respective case in proof of Theorem 1.
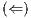 Let
Let 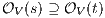 . Case
. Case 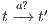 : we have to show there is
: we have to show there is 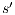 such that
such that 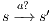 and
and 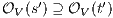 . If
. If 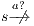 then
then 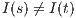 and therefore
and therefore 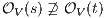 because
because 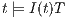 and
and 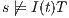 . Let
. Let 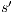 such that
such that 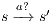 , notice
, notice 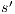 is unique because IA are input deterministic. If
is unique because IA are input deterministic. If 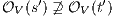 there is
there is 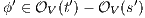 . This implies
. This implies 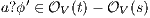 and we get a contradiction. In the case
and we get a contradiction. In the case 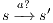 , we have to show there is
, we have to show there is 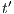 such that
such that 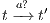 and
and 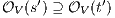 , this proof is similar to the previous one. Let now
, this proof is similar to the previous one. Let now 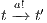 , we have to show there is
, we have to show there is 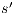 such that
such that 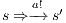 and
and 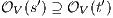 . Let
. Let 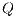 be
be 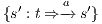 . If for all
. If for all 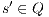 it holds
it holds 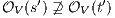 then there is
then there is 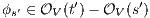 . Then for any
. Then for any 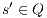 it holds
it holds 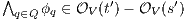 (at least one
(at least one 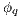 fails). But then
fails). But then 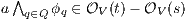 contradicting
contradicting 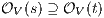 . Case
. Case 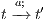 is analogous. __
is analogous. __
Now we are able show the statement.
Proof. If 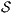 is SIR-SNNI then
is SIR-SNNI then 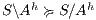 . By Theorem 6 we have
. By Theorem 6 we have 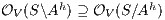 . On the other hand, by Lemma 1 we have
. On the other hand, by Lemma 1 we have 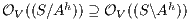 . Finally
. Finally 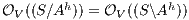 . The case
. The case 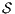 is SIR-NNI is analogous. __
is SIR-NNI is analogous. __
Two properties about SIR-NNI and SIR-SNNI were introduced in [9]. The first one, if an ISS is SIR-(S)NNI then it is (S)NNI. This is straightforward using their respective equivalent definition with notion of observability, ie 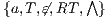 -(S)NNI and
-(S)NNI and 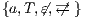 -(S)NNI. The second one, if an ISS is SIR-SNNI then it is SIR-NNI. This is a particular case of Theorem 3.
-(S)NNI. The second one, if an ISS is SIR-SNNI then it is SIR-NNI. This is a particular case of Theorem 3.
Theorem 5 shows that non-interference properties are not preserved for all notion of observation 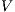 . This implies SIR-SNNI and SIR-NNI properties are not preserved by the composition.
. This implies SIR-SNNI and SIR-NNI properties are not preserved by the composition.
Despite this, we give sufficient conditions to ensure that the composition of ISS results in a non-interferent ISS (always with respect to SIR-SNNI and SIR-NNI). Basically, these conditions require that (i) the component ISS are fully compatible, i.e. no error state is reached in the composition (in any way, not only autonomously), and (ii) they do not use confidential actions to synchronize. This is stated in the following theorem.
Theorem 7. Let 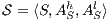 and
and 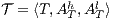 be two composable ISS such that
be two composable ISS such that 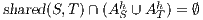 . If
. If 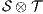 has no reachable error states and
has no reachable error states and 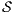 and
and 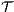 satisfy SIR-SNNI (resp. SIR-NNI) then
satisfy SIR-SNNI (resp. SIR-NNI) then 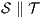 satisfies SIR-SNNI (resp. SIR-NNI).
satisfies SIR-SNNI (resp. SIR-NNI).
Proof. Define 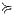 by
by 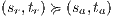 iff
iff 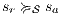 and
and 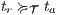 with
with 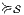 being a SIR between
being a SIR between 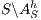 and
and 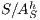 and similarly for
and similarly for 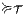 . We show that
. We show that 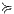 is a SIR between
is a SIR between 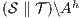 and
and 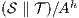 where
where 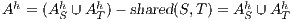 .
.
Suppose 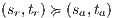 . We proceed by case analysis on the different transfer properties on Def 17. For case (a) suppose
. We proceed by case analysis on the different transfer properties on Def 17. For case (a) suppose 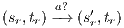 and
and 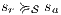 . Then there is
. Then there is 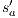 such that
such that 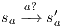 and
and 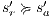 . As a consequence of the absence of error state in the product, we can ensure
. As a consequence of the absence of error state in the product, we can ensure 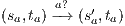 and
and 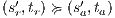 . The case
. The case 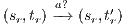 is analogous. In the same way we prove that condition (b) holds. For condition (c), let
is analogous. In the same way we prove that condition (b) holds. For condition (c), let 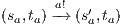 and
and 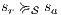 . Then there is
. Then there is 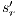 such that
such that 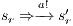 and
and 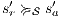 . Let
. Let 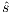 be a state s.t.
be a state s.t. 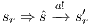 . Notice that all internal transition used to reach
. Notice that all internal transition used to reach 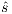 in
in 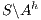 can be executed in
can be executed in 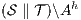 . Then
. Then 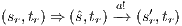 and
and 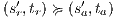 . The case
. The case 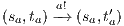 is analogous. We finally prove that condition (d) holds. Cases
is analogous. We finally prove that condition (d) holds. Cases 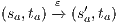 and
and 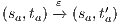 are similar to the previous one. Suppose now
are similar to the previous one. Suppose now 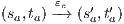 where
where 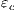 is an internal action resulting from a synchronization between
is an internal action resulting from a synchronization between 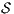 and
and 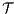 on common action
on common action 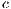 . Notice
. Notice 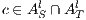 . W.l.o.g suppose
. W.l.o.g suppose 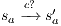 and
and 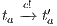 . Repeating previous reasoning, we can ensure there is state
. Repeating previous reasoning, we can ensure there is state 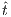 such that
such that 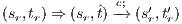 and
and 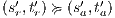 . __
. __
This result is useful when we develop all the components of a complex system. As we have total control of each component design, it is possible to achieve full compatibility. In this way, to ensure that the composed system is secure, we only have to develop secure components s.t. every high action of the component is a high action of the final system. This result can also be used when we are not in control of all components, i.e. we want use components not developed by us. The idea is simple, given two ISS, define the high actions used in the communication process as low and check if the resulting ISS satisfies the hypothesis of Theorem 7.
Corollary 1. Let 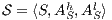 and
and 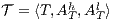 be two composable ISS. Let
be two composable ISS. Let 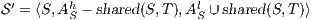 and
and 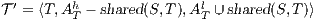 . If
. If 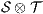 has no reachable error states and
has no reachable error states and 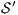 and
and 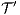 satisfy SIR-SNNI (resp. SIR-NNI) then
satisfy SIR-SNNI (resp. SIR-NNI) then 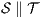 satisfies SIR-SNNI (resp. SIR-NNI).
satisfies SIR-SNNI (resp. SIR-NNI).
This result is based on the fact that actions used in the synchronization become hidden in the composition, then it is not important the confidential level of the actions.
5.2 Deriving Secure Interfaces
As we have seen, the composition of secure interfaces may yield a new insecure interface. This may happen when the components are already available but they were designed independently and they were not meant to interact. The question that arises then is if there is a way to derive a secure interface out of an insecure one. To derive the secure interface, we adapt the idea used to define ISS composition (see Def. 6); i.e. we restrict some input transitions in order to avoid insecure behavior. We then obtained a composed system that offers less services than the original one but is secure. In this section we present an algorithm to derive an ISS satisfying SIR-SNNI (or SIR-NNI) from a given ISS whenever possible. Since the method is similar in both cases, we focus on SIR-SNNI.
This algorithm is based on the algorithm presented in [6] to derive interfaces that satisfy BSNNI/BNNI, which in turn is based on the algorithm for bisimulation checking of [10]. The differences between both algorithm are consequence of the definition of SIR but the idea behind the procedure is the same. The new algorithm works as follows: given two interfaces 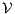 and
and 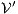 , the second without high actions, (i)
, the second without high actions, (i) 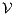 is semi-saturated adding all weak transitions
is semi-saturated adding all weak transitions 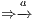 ; (ii) a semi-synchronous product of
; (ii) a semi-synchronous product of 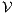 and
and 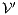 is constructed where transitions synchronize whenever they have the same label and satisfy some particular conditions; (iii) whenever there is a mismatching transition, a new transition is added on the product leading to a special fail state; (iv) if reaching a fail state is inevitable then
is constructed where transitions synchronize whenever they have the same label and satisfy some particular conditions; (iii) whenever there is a mismatching transition, a new transition is added on the product leading to a special fail state; (iv) if reaching a fail state is inevitable then 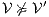 ; if there is always a way to avoid reaching a fail state, then
; if there is always a way to avoid reaching a fail state, then 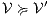 . We later define properly semi-saturation, semi-synchronous product and what means inevitably reaching a fail state. In this way, given an ISS
. We later define properly semi-saturation, semi-synchronous product and what means inevitably reaching a fail state. In this way, given an ISS 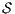 , we can check if
, we can check if 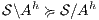 , if the check succeeds, then
, if the check succeeds, then 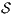 satisfies SIR-SNNI (see Theorem 8). If it does not succeed, then we provide an algorithm to decide whether
satisfies SIR-SNNI (see Theorem 8). If it does not succeed, then we provide an algorithm to decide whether 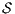 can be transformed into a secure ISS by controlling (i.e. pruning) input transitions. This decision mechanism categorizes insecure interfaces in two different classes: the class of interfaces that can surely be transformed into secure one and the class in which this is not possible.
can be transformed into a secure ISS by controlling (i.e. pruning) input transitions. This decision mechanism categorizes insecure interfaces in two different classes: the class of interfaces that can surely be transformed into secure one and the class in which this is not possible.
The algorithm to synthesize the secure ISS (once it is decided that it is possible) selects an input transition to prune, prune it, and checks whether the resulting ISS is secure. If it is not, a new input transition is selected and pruned. The process is repeated until it gets a secure interface. This process is shown to terminate (see Theorem 9).
Checking Strict Inputs Refinement. Different labels for internal actions do not play any role in a SIR relation. Then, to simplify, we replace all labels of internal action for two new ones: 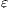 and
and 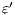 . The label
. The label 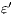 is used to represent an internal transition that can be removed; in our context, an internal action can be removed because it is a high input action that was hidden in order to check for security. Label
is used to represent an internal transition that can be removed; in our context, an internal action can be removed because it is a high input action that was hidden in order to check for security. Label 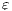 is used to identify internal action that cannot be removed. This is formalized in the following definition, which includes self-loops with
is used to identify internal action that cannot be removed. This is formalized in the following definition, which includes self-loops with 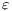 and
and 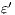 for future simplifications.
for future simplifications.
Definition 19. Let 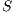 be an IA and
be an IA and 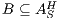 . Define
. Define 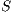 marking
marking 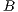 or marking
or marking 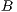 in
in 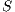 as the IA
as the IA 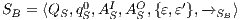 where
where  is the least relation satisfying following rules:
is the least relation satisfying following rules:
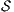 , the marking
, the marking  in
in  , notation
, notation  , is the ISS obtained after marking
, is the ISS obtained after marking  in the underlying IA.
in the underlying IA. A natural way to check weak bisimulation is to saturate the transition system i.e., to add a new transition 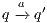 to the model for each weak transition
to the model for each weak transition 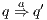 , and then checking strong bisimulation on the saturated transition system. Applying a similar idea we can check if there is a SIR relation. We add a transition
, and then checking strong bisimulation on the saturated transition system. Applying a similar idea we can check if there is a SIR relation. We add a transition 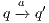 whenever
whenever 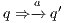 with
with 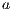 an output action. We call this process semi-saturation.
an output action. We call this process semi-saturation.
Definition 20. Let 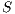 be an IA such that
be an IA such that 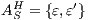 . The semi-saturation of
. The semi-saturation of 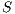 is the IA
is the IA 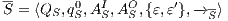 where
where 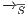 is the smallest relation satisfying the following rules:
is the smallest relation satisfying the following rules:
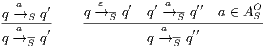
Given an ISS 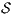 , its semi-saturation,
, its semi-saturation, 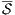 , is the ISS obtained by saturating the underlying IA.
, is the ISS obtained by saturating the underlying IA.
The last definition ensure that: if 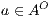 then
then 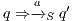 iff
iff 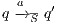 .
.
Following [6] and [10], the definition of the synchronous products follows from the conditions of the relation being checked, in this case SIR. First, we recapitulate these conditions and then we present the formal definition. If 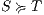 then for two states
then for two states 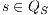 and
and 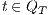 s.t.
s.t. 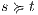 , every output/hidden action that
, every output/hidden action that 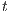 can execute has to be simulated by
can execute has to be simulated by 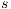 (probably using internal action); on the other hand,
(probably using internal action); on the other hand, 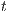 is not forced to simulate output/hidden actions from
is not forced to simulate output/hidden actions from 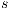 . Finally, both states have to simulate all input action that can be executed by the other one without performing previously any internal action. All these restrictions become evident from the definition of SIR. When a condition is not satisfied, a transition to a special state fail is created. Taking this into account we define the semi-synchronized product.
. Finally, both states have to simulate all input action that can be executed by the other one without performing previously any internal action. All these restrictions become evident from the definition of SIR. When a condition is not satisfied, a transition to a special state fail is created. Taking this into account we define the semi-synchronized product.
Definition 21. Let 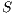 be a semi-saturated IA and
be a semi-saturated IA and 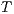 be an IA such that
be an IA such that  for
for  and
and 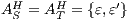 . The semi-synchronous product of
. The semi-synchronous product of 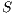 and
and 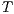 is the IA
is the IA 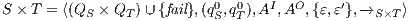 where
where 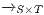 is the smallest relation satisfying following rules:
is the smallest relation satisfying following rules:
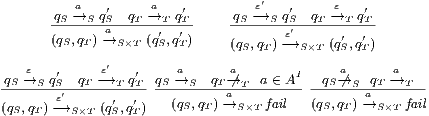
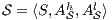 and
and 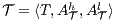 with
with 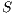 and
and 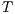 satisfying conditions above and
satisfying conditions above and 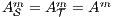 for
for  , then the semi-synchronous product of
, then the semi-synchronous product of  and
and  is defined by the ISS
is defined by the ISS 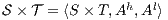 .
. Let us show how we can use synchronous product to check and derive, whenever it is possible, a SIR relation. If there is a state 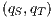 such that
such that 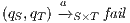 then it is evident that
then it is evident that 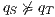 . Moreover, suppose the synchronous product only has states
. Moreover, suppose the synchronous product only has states 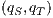 and
and 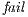 and the transition
and the transition 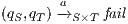 . If
. If 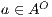 , as the progress from
, as the progress from 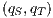 is autonomous, there is no way to control the execution of
is autonomous, there is no way to control the execution of 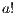 and hence there is no way to avoid
and hence there is no way to avoid 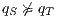 . Then, we say that
. Then, we say that 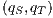 fails the SIR-relation test. On the other hand, if
fails the SIR-relation test. On the other hand, if 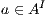 , a state offers a service that the other does not. In this case, removing the input transition
, a state offers a service that the other does not. In this case, removing the input transition 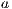 (the interface offers less services), we avoid transition
(the interface offers less services), we avoid transition 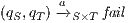 in the synchronous product and we get two states such that
in the synchronous product and we get two states such that 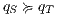 , moreover, we get two interfaces related by a SIR relation. In this case, we say that
, moreover, we get two interfaces related by a SIR relation. In this case, we say that 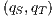 may pass the SIR relation test. In a more complex synchronous product, the “failure” in the state
may pass the SIR relation test. In a more complex synchronous product, the “failure” in the state 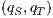 has to be propagated backwards appropriately to identify pairs of states that cannot be related. This propagation is done by the definitions of two different sets:
has to be propagated backwards appropriately to identify pairs of states that cannot be related. This propagation is done by the definitions of two different sets:  and
and  . The set
. The set  contains those pairs that are not related by a refinement and there is no set of input transitions to prune so that the pair may become related by the refinement. On the other hand,
contains those pairs that are not related by a refinement and there is no set of input transitions to prune so that the pair may become related by the refinement. On the other hand,  contains pairs of states that are not related but will be related if some transition is pruned. States not in
contains pairs of states that are not related but will be related if some transition is pruned. States not in 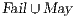 , belong to the set
, belong to the set 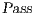 . All pairs in
. All pairs in 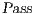 are related by a SIR relation.
are related by a SIR relation.
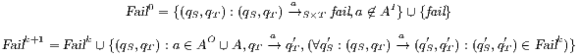
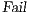 set.
set. 
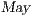 set .
set . Definition 22. Let 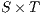 be a synchronous product. We define the sets
be a synchronous product. We define the sets 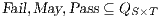 respectively by:
respectively by:
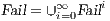 where
where 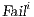 is defined in Table 3. If
is defined in Table 3. If 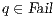 , we say that the pair
, we say that the pair 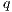 fails the SIR relation test.
fails the SIR relation test. 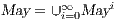 where
where 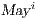 is defined in Table 4. If
is defined in Table 4. If 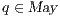 , we say that the pair
, we say that the pair 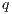 may pass the SIR relation test.
may pass the SIR relation test.  . If
. If 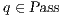 , we say that the pair
, we say that the pair 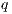 passes the SIR relation test
passes the SIR relation test
If the initial state of the underlying IA of an ISS 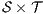 passes (may pass, fails) the SIR relation test, we say that
passes (may pass, fails) the SIR relation test, we say that 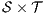 passes (may pass, fails) the SIR relation test.
passes (may pass, fails) the SIR relation test.
The proof of the following lemma is based on the proof of the algorithm to check bisimulation in [10], for this reason we only present a proof sketch. Our proof deviates a little from the original as a consequence of not all mismatching transitions are problematic.
Proof sketch. Since 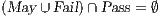 , we only have to prove that (i)
, we only have to prove that (i) 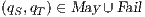 implies
implies 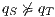 and (ii) if
and (ii) if 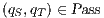 then
then 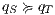 . The proof of (i) is by induction on
. The proof of (i) is by induction on 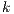 in
in 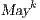 and
and 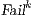 . The proof of (ii) is straightforward after showing that, given a state
. The proof of (ii) is straightforward after showing that, given a state 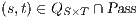 , then:
, then:
- 1.
- if
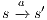 and
and 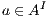 then there is a state
then there is a state 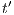 s.t. there is a transition
s.t. there is a transition 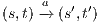 and
and 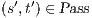 .
. - 2.
- if
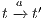 then there is a state
then there is a state 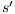 s.t. there is a transition
s.t. there is a transition 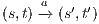 and
and 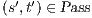 .
.
The proof of both statements is by case analysis on 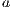 obtaining always a contradiction. __
obtaining always a contradiction. __
Using this lemma, we can verify if an interface is SIR-SNNI, since 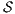 is SIR-SNNI if
is SIR-SNNI if 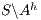 is refined by
is refined by 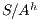 . Notice that we cannot use
. Notice that we cannot use 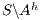 and
and 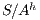 to create a semi-synchronized product; in general,
to create a semi-synchronized product; in general, 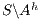 does not satisfy
does not satisfy 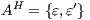 and it is not semi-saturated. This can be solved marking
and it is not semi-saturated. This can be solved marking 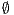 in
in 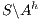 and then semi-saturating the interface, i.e. we work with
and then semi-saturating the interface, i.e. we work with 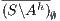 instead of
instead of 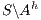 . Similarly,
. Similarly,  does not satisfy
does not satisfy 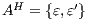 . Since
. Since 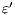 is used to represent the internal action that can be removed, we solve this problem marking
is used to represent the internal action that can be removed, we solve this problem marking 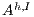 in
in 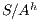 , i.e. we replace
, i.e. we replace 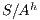 by
by 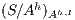 . Therefore, verifying that
. Therefore, verifying that 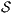 satisfies SIR-SNNI amounts to checking whether
satisfies SIR-SNNI amounts to checking whether 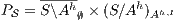 passes the refinement test. Applying a similar reasoning, if we are interested on verifying SIR-NNI, we can check if
passes the refinement test. Applying a similar reasoning, if we are interested on verifying SIR-NNI, we can check if 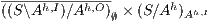 passes the SIR-relation test. Then we have a decision algorithm to check whether an ISS satisfies SIR-SNNI or SIR-NNI. We state it in the following theorem.
passes the SIR-relation test. Then we have a decision algorithm to check whether an ISS satisfies SIR-SNNI or SIR-NNI. We state it in the following theorem.
- 1.
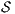 satisfies SIR-SNNI iff
satisfies SIR-SNNI iff 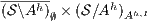 passes the SIR-relation test.
passes the SIR-relation test. - 2.
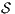 satisfies SIR-NNI iff
satisfies SIR-NNI iff 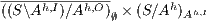 passes the SIR-relation test.
passes the SIR-relation test.
Synthesizing Secure ISS. In the following, we show that if a synchronized product 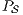 may pass the SIR relation test then there is a set of input transition that can be pruned so that the resulting interface is secure. First, we need to select which are the candidate input actions to be removed. So, if
may pass the SIR relation test then there is a set of input transition that can be pruned so that the resulting interface is secure. First, we need to select which are the candidate input actions to be removed. So, if 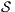 is an ISS such that
is an ISS such that  may pass the SIR-relation test, the set
may pass the SIR-relation test, the set 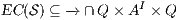 (see Table 5) is the set of eliminable candidates.
(see Table 5) is the set of eliminable candidates.
All transitions in 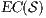 are involved in a synchronization that connects a source pair that may pass the SIR-relation test and a failing target. This can happen in four different situations. The first one is the basic case, in which one of the components of the pair can perform a low input transition that cannot be matched by the other. The following two cases are symmetric and consider the case in which both sides can perform an equally low input transition but end up in a failing state. The last case includes high input actions that are hidden in the synchronized product and always reach a pair that fails. Notice that if
are involved in a synchronization that connects a source pair that may pass the SIR-relation test and a failing target. This can happen in four different situations. The first one is the basic case, in which one of the components of the pair can perform a low input transition that cannot be matched by the other. The following two cases are symmetric and consider the case in which both sides can perform an equally low input transition but end up in a failing state. The last case includes high input actions that are hidden in the synchronized product and always reach a pair that fails. Notice that if 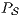 may pass the bisimulation test then
may pass the bisimulation test then 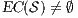 .
.
An important result is that no new failing pair of states is introduced by removing eliminable candidates. Moreover, if a pair of states fails in the synchronous product of the original ISS and it is also present in the synchronous product of the reduced ISS, then it also fails in this ISS. This ensures that a synchronous product that may pass the SIR-relation test, will not fail after pruning. In a sense, Lemma 4 below states that the sets 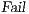 and
and 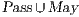 remain invariant.
remain invariant.
Lemma 4. Let  be an ISS s.t.
be an ISS s.t.  may pass the SIR-relation test. Let
may pass the SIR-relation test. Let 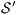 be an ISS obtained by removing one transition in
be an ISS obtained by removing one transition in 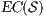 from
from 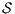 (i.e.
(i.e. 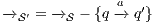 , provided
, provided 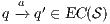 , and unreachable states are removed form
, and unreachable states are removed form 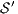 ). Then it holds that: (i)
). Then it holds that: (i) 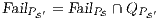 ; (ii)
; (ii) 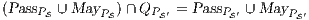 (Subindices in
(Subindices in 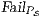 ,
, 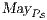 , etc. indicate that these sets were obtained from the synchronous product
, etc. indicate that these sets were obtained from the synchronous product 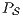 .)
.)
Proof. We only show (i). (ii) is an immediate consequence of (i).
(Case 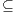 ). Clearly
). Clearly 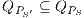 . Suppose
. Suppose 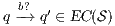 is the transition that is removed. By induction on
is the transition that is removed. By induction on 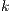 we show
we show 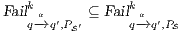 for all
for all 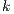 . This implies
. This implies 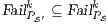 and then
and then 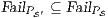 . Suppose
. Suppose 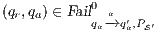 . By definition, action
. By definition, action 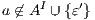 and
and 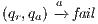 . Then
. Then  and therefore
and therefore  belongs to
belongs to 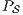 . Then
. Then 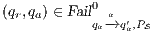 . Suppose now
. Suppose now 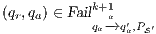 . Then
. Then 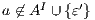 and
and 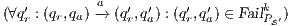 . Notice that
. Notice that 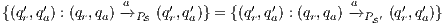 as consequence of
as consequence of 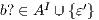 . By induction hypothesis
. By induction hypothesis 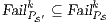 , then
, then 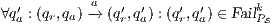 and we get
and we get 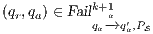 and
and 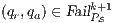 .
.
(Case 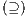 .) We show by induction on
.) We show by induction on 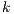 that
that 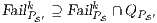 for all
for all 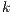 . Let
. Let 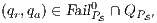 . Moreover, w.l.o.g. suppose
. Moreover, w.l.o.g. suppose 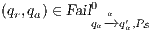 . Since
. Since 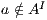 , the transition
, the transition 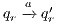 cannot be removed and since
cannot be removed and since 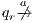 , then it holds that
, then it holds that 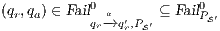 . For the induction case, suppose w.l.o.g.
. For the induction case, suppose w.l.o.g. 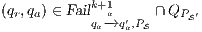 . Then
. Then 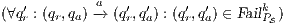 . Since
. Since  is reachable in
is reachable in 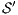 and
and 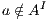 , all pair
, all pair 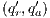 is reachable in
is reachable in 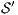 . By induction hypothesis,
. By induction hypothesis, 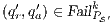 and then
and then 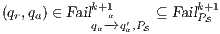 . __
. __
The following theorem is the main result of this section. Notice that its proof defines the algorithm to prune input actions and obtain a secure interface. A similar result holds for SIR-NNI.
Theorem 9. Let 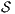 be an ISS such that
be an ISS such that 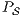 may pass the SIR relation test. Then there is an input transition set
may pass the SIR relation test. Then there is an input transition set  such that, if
such that, if  is the ISS obtained from
is the ISS obtained from  by removing all transitions in
by removing all transitions in  ,
, 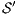 is SIR-SNNI.
is SIR-SNNI.
Proof. We only report a proof sketch. The complete proof follows in the same way as the proof of Theorem 4.10 in [6]. Let 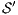 be an ISS obtained from
be an ISS obtained from 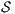 by removing one transition from the set
by removing one transition from the set 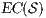 . Lemma 4 ensures that
. Lemma 4 ensures that  may pass or passes the SIR relation test. If
may pass or passes the SIR relation test. If  passes the SIR relation test, we stop. If
passes the SIR relation test, we stop. If  may pass the SIR relation test, we repeat the process until we obtain an ISS that passes the test. Since the transition set is finite, in the worst case, we will continue with the process until obtaining an ISS with an empty set of eliminable candidates. If this ISS may pass the SIR-relation test we get a contradiction with the fact that the set of eliminable candidates is empty, then this ISS has to pass the test. Finally,
may pass the SIR relation test, we repeat the process until we obtain an ISS that passes the test. Since the transition set is finite, in the worst case, we will continue with the process until obtaining an ISS with an empty set of eliminable candidates. If this ISS may pass the SIR-relation test we get a contradiction with the fact that the set of eliminable candidates is empty, then this ISS has to pass the test. Finally, 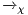 is composed by the set of transitions removed along the way. __
is composed by the set of transitions removed along the way. __
In this work, we have presented semantics for interactive sequential systems. In this way we have extended the work of [1] and [2] to models where the control of the actions is shared by the user and the system. To reduce complexity, we did not include all types of observations presented in [2], thus limiting ourselves to work with a subset of them. We do not foresee major problems in extending our theory to the types of observations we left out.
The approach to define non-interference security properties through types of observations gives important insight about the security model, in particular about the characteristics of the attacker. For instance, if the attacker can make use of the covert channels, then the type of observation 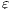 should be chosen. Another example is the type of observation
should be chosen. Another example is the type of observation 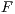 which can be interpreted as the system detecting an attack and aborting the execution. In this way, the types of observations define a catalogue to characterize the attackers that could be considered.
which can be interpreted as the system detecting an attack and aborting the execution. In this way, the types of observations define a catalogue to characterize the attackers that could be considered.
This general definition encloses previous definitions of non-interference for ISS. We found notions of observability to represent (S)NNI, B(S)NNI and SIR-(S)NNI (Theorem 1 and Lemma 2). This approach also provides a better understanding of the security properties. In [9], SIR-(S)NNI is introduced to resolve some shortcomings found in B(S)NNI, but in fact, these shortcomings do not exist because the properties should be considered in a different context. B(S)NNI should be considered in a context where an attacker can only observes how the system behaves. On the other hand, SIR-(S)NNI should be considered in a context where the attacker can interact through the interface. This is obvious when we see the notions of observability used to represent each property: 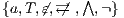 for B(S)NNI and
for B(S)NNI and 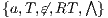 for SIR-(S)NNI. Notice that B(S)NNI has the no interaction type
for SIR-(S)NNI. Notice that B(S)NNI has the no interaction type 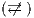 while in SIR-(S)NNI the interaction is explicit due to the type
while in SIR-(S)NNI the interaction is explicit due to the type 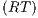 .
.
In addition, the different types of observations provide a simple way to chose the appropriate notion of security. For example notice interface  in Figure 5. One could argue that still there is an information leakage, because the execution of action
in Figure 5. One could argue that still there is an information leakage, because the execution of action  is an evidence that the high user has not interacted with the interface. If this information is sensitive and the attacker interacts with the interface, one could use the notion of observability
is an evidence that the high user has not interacted with the interface. If this information is sensitive and the attacker interacts with the interface, one could use the notion of observability 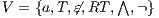 to detect this kind of problem. Notice this notion of observability is stronger than the notion used for B(S)NNI.
to detect this kind of problem. Notice this notion of observability is stronger than the notion used for B(S)NNI.
Future Works. We have identified two different research lines to continue this work. At first place, the types of observations presented in [2] that have been omitted, have to be addressed, and a deep study comparing the different semantics should be carried out to get a better understanding of them. Second, we also plan to study how the new semantics for interactive systems affect the different models with both input/controllable and output/uncontrollable actions and the results obtained for them.
[1] R. J. V. Glabbeek, “The linear time - branching time spectrum i. the semantics of concrete, sequential processes,” in In Handbook of Process Algebra. Elsevier, 2001, pp. 3–99.
[2] R. van Glabbeek, “The linear time-branching time spectrum II: The semantics of sequential processes with silent moves,” in Proceedings CONCUR, vol. 93, 2003, pp. 66–81.
[3] L. de Alfaro and T. A. Henzinger, “Interface theories for component-based design,” in EMSOFT, ser. LNCS, T. A. Henzinger and C. M. Kirsch, Eds., vol. 2211. Springer, 2001.
[4] L. de Alfaro and T. Henzinger, “Interface automata,” in ESEC / SIGSOFT FSE. ACM Press, 2001, pp. 109–120.
[5] L. de Alfaro and T. A. Henzinger, “Interface-based design,” in Engineering Theories of Software-Intensive Systems, ser. Nato Science Series, M. B. et al., Ed. Springer, 2005, pp. 83–104.
[6] M. Lee and P. R. D’Argenio, “Describing secure interfaces with interface automata,” Electron. Notes Theor. Comput. Sci., vol. 264, no. 1, pp. 107–123, 2010.
[7] J. A. Goguen and J. Meseguer, “Security policies and security models,” in IEEE Symposium on Security and Privacy, 1982, pp. 11–20.
[8] R. Focardi and R. Gorrieri, “Classification of security properties (part i: Information flow),” in Procs. of FOSAD 2000, ser. LNCS, vol. 2171. Springer, 2001, pp. 331–396.
[9] M. Lee and P. R. D’Argenio, “A refinement based notion of non-interference for interface automata: Compositionality, decidability and synthesis,” in SCCC, 2010, pp. 280–289.
[10] J.-C. Fernandez and L. Mounier, ““On the fly” verification of behavioural equivalences and preorders,” in Procs. of CAV ’91, ser. LNCS, vol. 575. Springer, 1991, pp. 181–191.