Services on Demand
Journal
Article
Related links
Share
CLEI Electronic Journal
On-line version ISSN 0717-5000
CLEIej vol.14 no.1 Montevideo Apr. 2011
Abstract
We tackle the numerical simulation of reaction-diffusion equations modeling multi-scale reaction waves. This type of problems induces peculiar difficulties and potentially large stiffness which stem from the broad spectrum of temporal scales in the nonlinear chemical source term as well as from the presence of large spatial gradients in the reaction fronts, spatially very localized. In this paper, we introduce a new resolution strategy based on time operator splitting and space adaptive multiresolution in the context of very localized and stiff reaction fronts. Based on recent theoretical studies of numerical analysis, such a strategy leads to a splitting time step which is not restricted neither by the fastest scales in the source term nor by restrictive diffusive step stability limits, but only by the physics of the phenomenon. We thus aim at solving accurately complete models including all time and space scales of the phenomenon, considering large simulation domains with conventional computing resources. The efficiency is evaluated through the numerical simulation of configurations which were so far out of reach of standard methods in the field of nonlinear chemical dynamics for 2D spiral waves and 3D scroll waves as an illustration. Future extensions of the proposed strategy are finally discussed.
Spanish abstract
Estudiamos la simulación numérica de ecuaciones de reacción-difusión que modelan ondas de reacción multi-escala. Este tipo de problemas induce dificultades peculiares y problemas de condicionamiento potencialmente grandes que surgen del amplio espectro de escalas temporales en el término no-lineal de la fuente química y de la presencia de grandes gradientes espaciales en el frente de reacción, muy localizados espacialmente. En este trabajo, introducimos una nueva estrategia de resolución basada en el particionamiento del operador temporal y en la multiresolución adaptiva espacial. Sobre la base de estudios teóricos recientes en el campo de análisis numérico, esta estrategia conduce a un paso de tiempo que no está restringido por las escalas más veloces en el término fuente ni por límites de estabilidad en la etapa de difusión, sino sólo por la propia física del fenómeno en estudio. De esta forma pretendemos resolver de forma precisa modelos completos que incluyen todas las escalas espaciales y temporales del fenómeno, teniendo en cuenta dominios de simulación amplios utilizando recursos computacionales convencionales. La eficiencia se evalúa a través de la simulación numérica de configuraciones que hasta el momento estaban fuera del alcance de los métodos estándar en el campo de la dinámica química no lineal para ondas espiral 2D y ondas scroll 3D. Extensiones futuras de la estrategia se discuten al final.
Keywords: Reaction-diffusion, multi-scale waves, operator splitting, adaptive multiresolution.
Spanish keywords: difusión-reacción, ondas multi-escala, división de operadores, multiresolución adaptativa.
Numerical simulations of multi-scale phenomena are commonly used for modeling purposes in many applications such as combustion, chemical vapor deposition, or air pollution modeling. In general, all these models raise several difficulties created by the large number of unknowns and the wide range of temporal scales due to large and detailed chemical kinetic mechanisms, as well as steep spatial gradients associated with very localized fronts of high chemical activity. Furthermore, a natural stumbling block to perform 3D simulations is the unreasonable memory requirements of standard numerical strategies for time dependent problems.
The most natural idea to overcome these difficulties is to use dedicated numerical methods and to solve the complete models where diffusion, reaction and eventually convection are coupled together. One aims at solving strongly coupled nonlinear systems with either a fully implicit method, or yet semi-implicit or linearized implicit methods instead (see [1] and references therein). However, the strong stability restrictions for the latter when dealing with very fast temporal scales, as well as the computing cost and the huge memory requirements of these methods, even if adaptive grids are used, make of these strategies difficult to be handled.
An alternative numerical strategy is then to combine implicit and explicit schemes to discretize nonlinear evolution problems in time. Further studies settled the appropriate numerical background for these methods called IMEX, which in particular might be conceived to solve stiff nonlinear problems [2, 3]. These methods are usually very efficient. Nevertheless, on the one hand, the feasibility of utilizing dedicated implicit solvers over a discretized domain becomes soon critical when treating large computational domains. And on the other hand, the time steps globally imposed over partial regions or the entire domain are strongly limited by either the stability restrictions of the explicit solver or by the fastest scales treated by the implicit scheme.
However, in many multi-scale problems, the fastest time scales do not play a leading role in the global physical phenomenon and thus, we might consider the possibility of using reduced models where these chemical scales have been previously relaxed. These simplified models provide reasonable predictions and the associated computing costs are significantly reduced in comparison with comprehensive chemical models. Nevertheless, these reduced models provide only approximate solutions and are usually accessible when the system is well-partitioned and the fastest scales can be identified or isolated, a process that in realistic configurations, relies on sensitivity analysis which is most of the time difficult to conduct and justify.
It is then natural to envision a compromise, since the resolution of the fully coupled problem is most of the time out of reach and the appropriate definition of reduced models is normally difficult to establish. In this context, time operator splitting methods have been used for a long time and there exists a large literature showing the efficiency of such methods for evolution problems. In practice, it is firstly necessary to decouple numerically the reaction part from the rest of the physical phenomena like convection, diffusion or both, for which there also exist dedicated numerical methods. Hence, these techniques allow a completely independent optimization of the resolution of each subsystem which usually yields lower requirements of computing resources.
In the context of multi-scale waves, the dedicated methods chosen for each subsystem are then responsible for dealing with the fastest scales associated with each one of them, in a separate manner; then, the composition of the global solution based on the splitting scheme should guarantee the good description of the global physical coupling. A rigorous numerical analysis is therefore required to better establish the conditions for which the latter fundamental constraint is verified. As a matter of fact, several works [4, 5, 1] proved that the standard numerical analysis of splitting schemes fails in the presence of scales much faster than the splitting time step and motivated more rigorous studies for these stiff configurations [6, 7] and in the case where spatial multi-scale phenomena arise as a consequence of steep spatial gradients [8].
We therefore introduce a new operator splitting strategy, based on these theoretical results, that considers on the one hand, a high order method like Radau5 [9], based on implicit Runge-Kutta schemes for stiff ODEs, to solve the reaction term; and on the other hand, another high order method like ROCK4 [10], based on explicit stabilized Runge-Kutta schemes, to solve the diffusion problem. Finally, the proposed numerical strategy is complemented by a mesh refinement technique based on Harten’s pioneering work on adaptive multiresolution methods [11], being aware of the interest of adaptive mesh techniques for propagating waves exhibiting spatial multi-scale phenomena due to locally steep spatial gradients. The main goal is then to perform feasible and accurate in time and space simulations of the complete dynamics of multi-scale phenomena under study with accuracy control of the solution and splitting time steps purely dictated by the physics of the phenomenon and not by any stability constraints associated with mesh size or source time scales.
The paper is organized as follows: In Section 2, we first recall the time operator splitting schemes to then describe the construction of an optimal operator splitting scheme for multi-scale problems, and its coupling with a suitable grid adaptation strategy, the space adaptive multiresolution technique [12, 13]. 2D and 3D simulations of a three species reaction-diffusion system modeling the Belousov-Zhabotinsky reaction are presented in Section 3 to illustrate the potential and performance of the method, after a short 1D study of splitting errors for stiff problems. We end in section 4 with some concluding remarks and future works.
2 Construction of the Numerical Strategy
In this section, we introduce a new splitting strategy for multi-scale waves modeled by stiff reaction-diffusion systems. Once established the time integration strategy, we detail briefly the adaptive multiresolution method that we have implemented as mesh refinement technique for this new resolution technique.
Let us first set the general mathematical framework in this work. A class of multi-scale phenomena are modeled by general reaction-diffusion systems like:
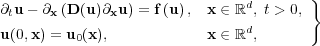 | (1) |
where 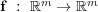 and
and 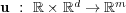 , with the diffusion matrix
, with the diffusion matrix 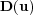 , which is a tensor of order
, which is a tensor of order 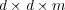 .
.
In order to simplify the presentation, we consider problem (1) with linear diagonal diffusion, in which case the elements of the diffusion matrix are written as 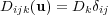 , so that the diffusion operator reduces to the heat operator with scalar diffusion coefficient
, so that the diffusion operator reduces to the heat operator with scalar diffusion coefficient 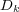 for component
for component 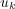 of
of 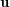 ,
, 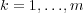 . In any case, the proposed numerical strategy normally deals with general problem (1). Performing a fine spatial discretization, we obtain the semi-discretized initial value problem:
. In any case, the proposed numerical strategy normally deals with general problem (1). Performing a fine spatial discretization, we obtain the semi-discretized initial value problem:
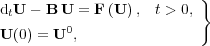 | (2) |
where 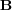 corresponds to the discretization of the Laplacian operator with the coefficients
corresponds to the discretization of the Laplacian operator with the coefficients 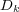 within;
within;  and
and 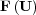 are arranged component-wise all over the discretized spatial domain. Considering a standard decoupling of the diffusion and reaction parts of (2), we denote
are arranged component-wise all over the discretized spatial domain. Considering a standard decoupling of the diffusion and reaction parts of (2), we denote 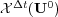 as the numerical solution of the discretized diffusion equation:
as the numerical solution of the discretized diffusion equation:
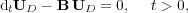 | (3) |
with initial data 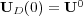 after an integration time step
after an integration time step 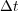 . We also denote by
. We also denote by 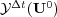 the numerical solution of the reaction part:
the numerical solution of the reaction part:
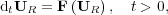 | (4) |
with initial data 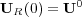 .
.
The two Lie approximation formulae of the solution of system (2) are then defined by
 | (5) |
whereas the two Strang approximation formulae [14] are given by
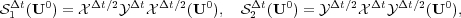 | (6) |
where 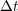 is now the splitting time step. It is well known that Lie formulae (5) (resp. Strang formulae (6)) are approximations of order
is now the splitting time step. It is well known that Lie formulae (5) (resp. Strang formulae (6)) are approximations of order 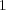 (resp.
(resp.  ) of the exact solution of (2) in the case where
) of the exact solution of (2) in the case where 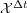 and
and 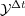 are the exact solutions
are the exact solutions 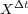 and
and 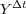 of problems (3) and (4). Then, appropriate numerical approximations of
of problems (3) and (4). Then, appropriate numerical approximations of 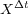 and
and 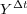 are required in order to compute Lie and Strang formulae with the prescribed order.
are required in order to compute Lie and Strang formulae with the prescribed order.
Higher order splitting configurations are also possible. Nevertheless, the order conditions for such composition methods state that either negative time substeps or complex coefficients are necessary (see [9]). The formers imply normally important stability restrictions and more sophisticated numerical implementations. In the particular case of negative time steps, they are completely undesirable for PDEs that are ill-posed for negative time progression.
The standard orders achieved with a Lie or Strang scheme are no longer valid when we consider very stiff reactive or diffusive terms (see [6]). Furthermore, if the fastest time scales play a leading role in the global physics of the phenomenon, then the solution obtained by means of a splitting composition scheme will surely fail to capture the global dynamics of the phenomenon, unless we consider splitting time steps small enough to resolve such scales.
In the opposite case where these fast scales are not directly related to the physical evolution of the phenomenon, larger splitting time steps might be considered, but order reductions may then appear due to short-life transients associated with the fastest variables. This is usually the case for propagating reaction waves where for instance, the speed of propagation is much slower than the chemical scales. In this context, it has been proved in [6] that better performances are expected while ending the splitting scheme by the time integration of the reaction part (4):
where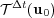 stands for the exact solution of (1) with linear diagonal diffusion, and the fastest scales are present in the reactive term. In a general case, the splitting scheme should always end with the part involving the fastest time scales of the phenomenon (see a numerical case in [7]).
stands for the exact solution of (1) with linear diagonal diffusion, and the fastest scales are present in the reactive term. In a general case, the splitting scheme should always end with the part involving the fastest time scales of the phenomenon (see a numerical case in [7]). On the other hand, one must also take into account possible order reductions coming this time from space multi-scale phenomena due to steep spatial gradients whenever large splitting time steps are considered, as analyzed in [8]:
for which the first terms are more relevant when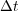 is small and the second ones when
is small and the second ones when 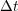 is not small enough and
is not small enough and 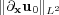 is very high.
is very high. These theoretical studies allow to depict more precisely the approximation errors of the splitting techniques and thus, help us to select among the various splitting alternatives, depending on the nature of the problem. Nevertheless, the choice of suitable time integration methods for each subsystem is mandatory not only to guarantee such theoretical estimates but also to take advantage of the particular features of each independent subproblem in order to solve them with reasonable resources as accurately as possible. In particular, our splitting technique considers high order dedicated integration methods for each subproblem in order to properly solve the fastest time scales associated with each one of them, and in such a way that the main source of error is led by the operator splitting error. Then, the control of the accuracy of the simulation is ruled by the splitting scheme approximation through the decoupling time step needed to describe the global physical phenomenon within a required level of accuracy.
2.2.1 Time Integration of the Reaction: Radau5
Radau5 [9] is a high order method (formally of order  , which at worst might be reduced to
, which at worst might be reduced to 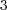 ) that is not only an A-stable method, but also L-stable, so that very stiff systems of ODEs might be solved without any stability problem. It considers also an adaptive time stepping strategy which guarantees a requested accuracy of the numerical integration and at the same time, allows to discriminate stiff zones from regular ones; hence, smaller time steps correspond to stiffer behaviors.
) that is not only an A-stable method, but also L-stable, so that very stiff systems of ODEs might be solved without any stability problem. It considers also an adaptive time stepping strategy which guarantees a requested accuracy of the numerical integration and at the same time, allows to discriminate stiff zones from regular ones; hence, smaller time steps correspond to stiffer behaviors.
Nevertheless, this high order method is achieved thanks to an implicit Runge-Kutta scheme. This means that in a general case, nonlinear systems must be solved throughout the time integration process. Even if the system resolution tools are highly optimized (which are based on modified Newton’s methods), these procedures become very expensive for large systems and important memory requirements are needed in order to carry out these computations. As a consequence, the size of the system of equations to be solved is strongly limited by the computing resources. However, in a splitting scheme context, we easily overcome this difficulty because the reactive term of (2) is a system of ODEs without spatial coupling. Therefore, a local approach node by node is adopted where the memory requirements are only set by the number of local unknowns, which normally does not exceed conventional memory resources. Even more, this approach is posed as an embarrassingly parallel problem where no data exchange is needed among nodes, that yields optimal load balancing on shared memory architectures (see for example the numerical implementations achieved in [15]).
Another important feature of this strategy is that precious computation time is saved because we adapt the time integration step only at nodes where the reaction phenomenon takes place. For multi-scale reaction waves, this happens in a very low percentage of the spatial domain, normally only in the neighborhood of the wavefront. Therefore, larger time steps are considered at nodes with a chemistry at (partial) equilibrium. This would not be possible if we integrated the entire reaction-diffusion system (2) at once.
2.2.2 Time Integration of the Diffusion: ROCK4
If we now consider ROCK4 [10], we recall that one of the most important advantages of such method is its explicit character, hence the simplicity of its implementation. In fact, no sophisticated Linear Algebra tools are needed (no resolution of linear systems required) and thus, the resolution is based on simple matrix-vector products. Nevertheless, the computation cost relies directly on the requested quantity of such products, that is the number of internal stages  needed over one time integration step
needed over one time integration step 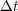 . The memory requirements are also reduced as a consequence of its explicit scheme; nevertheless we must keep in mind that these requirements increase proportionally with the number of nodes considered over the spatial domain.
. The memory requirements are also reduced as a consequence of its explicit scheme; nevertheless we must keep in mind that these requirements increase proportionally with the number of nodes considered over the spatial domain.
ROCK4 is formally a fourth order stabilized explicit Runge-Kutta method and such methods feature extended stability domain along the negative real axis. Therefore, in order to guarantee stability for a fixed time step 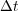 , the number of stages
, the number of stages  needed is directly related to the spectral radius
needed is directly related to the spectral radius 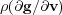 , considering a general problem such as
, considering a general problem such as 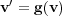 , since it should verify:
, since it should verify:
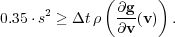
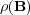 . In our particular applications, the diffusive phenomenon has a leading role of propagator of perturbations over the (partial) equilibrium nodes that result on excitation of the reactive schemes and thus, the propagation of the reaction wave. The resulting self-similar character implies that the number of stages needed will remain practically constant throughout the evolution of the phenomenon. The spectral radius must be previously estimated (for example, using the Gershgoring theorem or even numerically, as proposed by the ROCK4 solver by means of a nonlinear power method). Once again, the implementation of this diffusion solver over the entire reaction-diffusion system (2) will not be appropriate under neither theoretical nor practical considerations, and highlights the inherited advantages of operator splitting.
. In our particular applications, the diffusive phenomenon has a leading role of propagator of perturbations over the (partial) equilibrium nodes that result on excitation of the reactive schemes and thus, the propagation of the reaction wave. The resulting self-similar character implies that the number of stages needed will remain practically constant throughout the evolution of the phenomenon. The spectral radius must be previously estimated (for example, using the Gershgoring theorem or even numerically, as proposed by the ROCK4 solver by means of a nonlinear power method). Once again, the implementation of this diffusion solver over the entire reaction-diffusion system (2) will not be appropriate under neither theoretical nor practical considerations, and highlights the inherited advantages of operator splitting.
We are concerned with the propagation of reacting wavefronts, hence important reactive activity as well as steep spatial gradients are localized phenomena. This implies that if we consider the resolution of reactive problem (4), a considerable amount of computing time is spent on nodes without any chemical activity (see for example a precise computing time evaluation in [15]). Moreover, there is no need to represent these quasi-stationary regions with the same spatial discretization needed to describe the reacting wavefront, so that the diffusion problem (3) might also be solved over a smaller number of nodes. An adapted mesh obtained by a multiresolution process [12, 13] then turn out to be a very convenient solution to overcome these difficulties.
Therefore, let us consider a set of nested spatial grids  with
with 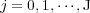 , from the coarsest to the finest one. A multiresolution transformation allows to represent a discretized function as values on a coarser grid plus a series of local estimates at different levels of such nested grids. These estimates correspond to the wavelet coefficients of a wavelet decomposition obtained by inter-level transformations, and retain the information on local regularity when going from a coarse to a finer grid. Hence, the main idea is to use the decay of the wavelet coefficients to obtain information on the local regularity of the solution: lower wavelet coefficients are associated with local regular spatial configurations and vice-versa.
, from the coarsest to the finest one. A multiresolution transformation allows to represent a discretized function as values on a coarser grid plus a series of local estimates at different levels of such nested grids. These estimates correspond to the wavelet coefficients of a wavelet decomposition obtained by inter-level transformations, and retain the information on local regularity when going from a coarse to a finer grid. Hence, the main idea is to use the decay of the wavelet coefficients to obtain information on the local regularity of the solution: lower wavelet coefficients are associated with local regular spatial configurations and vice-versa.
This representation leads to a thresholding process that builds dynamically the corresponding adapted grid on which the solutions are represented. The approximation errors of these adapted representations obtained by multiresolution transformation are then proportional to  , where
, where  is the threshold parameter that establishes the level of spatial regularity that does not need to be represented on the finest grid [11, 16]. In this way, our strategy aims at multiresolution errors of the spatial representation settled by
is the threshold parameter that establishes the level of spatial regularity that does not need to be represented on the finest grid [11, 16]. In this way, our strategy aims at multiresolution errors of the spatial representation settled by  , lower that the splitting approximation errors in order to control the level of accuracy of the simulation out of this combination of methods.
, lower that the splitting approximation errors in order to control the level of accuracy of the simulation out of this combination of methods.
In this last section, we present some numerical illustrations of the proposed strategy. A problem coming from nonlinear chemical dynamics is described and treated. First of all, we conduct a short illustration of the behavior of splitting errors in the context of time-space stiff propagating waves. The performance of the method is discussed based on a 2D simulation for which the accuracy of the simulation can be evaluated. Finally, a 3D simulation allows to illustrate the feasibility of solving large simulation domains with conventional computing resources.
3.1 Mathematical Model of Study
We are concerned with the numerical approximation of a model of the Belousov-Zhabotinski reaction, a catalyzed oxidation of an organic species by acid bromated ion (for more details and illustrations, see [17]). We thus consider the model introduced in [18] and coming from the classic work of Field, Koros and Noyes (FKN) (1972), which takes into account three species: 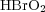 (hypobromous acid), bromide ions
(hypobromous acid), bromide ions 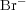 and cerium(IV). Denoting by
and cerium(IV). Denoting by ![a = [Ce (IV)]](/img/revistas/cleiej/v14n1/1a0756x.png) ,
, ![b = [HBrO2 ]](/img/revistas/cleiej/v14n1/1a0757x.png) and
and ![c = [Br- ]](/img/revistas/cleiej/v14n1/1a0758x.png) , we obtain a very stiff system of three partial differential equations:
, we obtain a very stiff system of three partial differential equations:
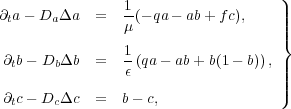 | (13) |
with diffusion coefficients 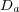 ,
, 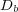 and
and 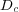 , and some real positive parameters
, and some real positive parameters 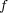 , small
, small  , and small
, and small  ,
, 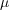 , such that
, such that 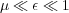 .
.
The dynamical system associated with this system models reactive excitable media with a large time scale spectrum (see [18] for more details). Moreover, the spatial configuration with addition of diffusion generates propagating wavefronts with steep spatial gradients. Hence, this model presents all the difficulties associated with a stiff multi-scale configuration. Even though the system structure allows an eventual discrimination of slow and fast variables, and thus other numerical strategies as partitioning methods might be considered [19], in this work we are not interested in performing such decomposition in order to remain consistent with more complex models for which such decomposition becomes complicated, as it was discussed in the Introduction. The advantages of applying a splitting strategy to these models have already been studied and presented in [20]. In what follows, we will briefly consider a 1D case of (13) in order to illustrate the errors of splitting schemes for stiff problems, then 2D and 3D configurations will be implemented.
In this part, we perform a short illustrating study of the behavior of splitting schemes when dealing with stiff problems as it was explained in  2.2. In the BZ model, stiffness is given by fast time scales as well as steep spatial gradients; we consider then a 1D configuration of problem (13) with homogeneous Neumann boundary conditions and the following parameters, taken from [18]:
2.2. In the BZ model, stiffness is given by fast time scales as well as steep spatial gradients; we consider then a 1D configuration of problem (13) with homogeneous Neumann boundary conditions and the following parameters, taken from [18]: 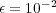 ,
, 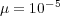 ,
, 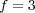 and
and 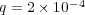 , with diffusion coefficients
, with diffusion coefficients 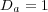 ,
, 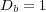 and
and 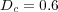 , for a space region of
, for a space region of ![[0,80]](/img/revistas/cleiej/v14n1/1a0776x.png) . A uniform mesh of
. A uniform mesh of 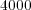 points is considered while exact solution
points is considered while exact solution  is approximated by a reference or quasi-exact solution of coupled reaction-diffusion problem (13) performed by Radau5 with very fine tolerances. Splitting schemes consider Radau5 and ROCK4 as resolution methods for reaction and diffusion problems as it was presented in
is approximated by a reference or quasi-exact solution of coupled reaction-diffusion problem (13) performed by Radau5 with very fine tolerances. Splitting schemes consider Radau5 and ROCK4 as resolution methods for reaction and diffusion problems as it was presented in  2.2.
2.2.


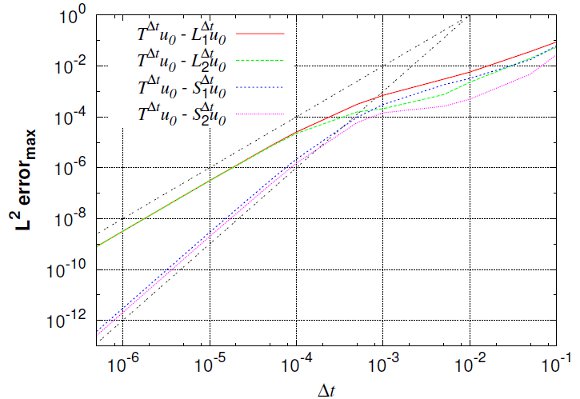
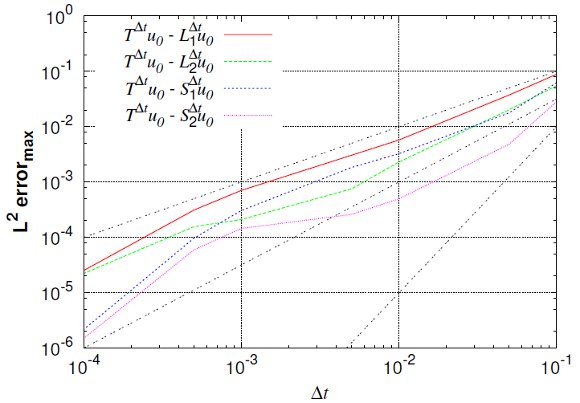
 and
and 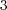 are depicted (left), and slopes
are depicted (left), and slopes 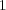 ,
, 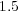 and
and 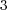 in the zoomed loss order region (right)
in the zoomed loss order region (right)
Figure 1 shows that both Lie and Strang schemes have asymptoticly local order 2 and 3 for small time steps. Nevertheless, for larger time steps, previous studies in [6] and [8] describe better the numerical behavior of these schemes. For 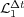 , order
, order  drops to
drops to 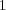 as predicted by (7); whereas for
as predicted by (7); whereas for 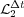 , we see the influence of spatial gradients as predicted by (11) and thus, order
, we see the influence of spatial gradients as predicted by (11) and thus, order 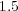 is recovered after some transition phase. Same conclusions are drawn for Strang schemes, order of
is recovered after some transition phase. Same conclusions are drawn for Strang schemes, order of 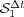 drops from
drops from 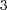 to
to 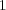 according to (8), while for
according to (8), while for 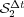 , we see the influence of steep spatial gradients that alter the order
, we see the influence of steep spatial gradients that alter the order 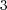 given by (10). Maximum
given by (10). Maximum 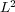 error considers the maximum value between computed normalized local errors for
error considers the maximum value between computed normalized local errors for  ,
,  and
and  variables; in these numerical tests, it corresponds to variable
variables; in these numerical tests, it corresponds to variable  . Finally, in all cases the reaction ending schemes show better behaviors for larger splitting time steps, according to [6]. In particular,
. Finally, in all cases the reaction ending schemes show better behaviors for larger splitting time steps, according to [6]. In particular, 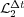 behaves even better than
behaves even better than 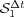 , whereas
, whereas 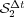 is the best alternative for all time steps.
is the best alternative for all time steps.
We consider now the 2D application of problem (13) with homogeneous Neumann boundary conditions and the following parameters, taken from a preliminary study [20]: 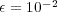 ,
, 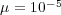 ,
, 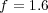 and
and 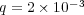 , with diffusion coefficients
, with diffusion coefficients 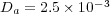 ,
, 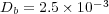 and
and 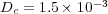 . The phenomenon is studied over a time domain of
. The phenomenon is studied over a time domain of ![[0,4]](/img/revistas/cleiej/v14n1/1a07112x.png) and a space region of
and a space region of ![[0,1]× [0,1]](/img/revistas/cleiej/v14n1/1a07113x.png) .
.
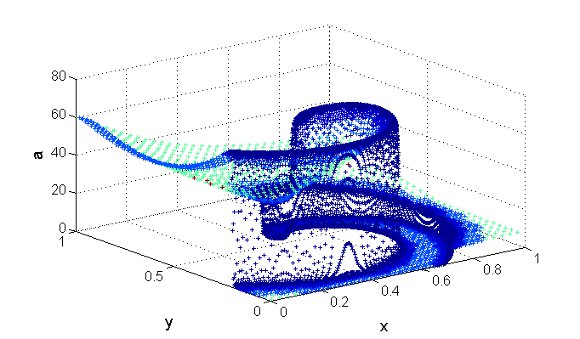
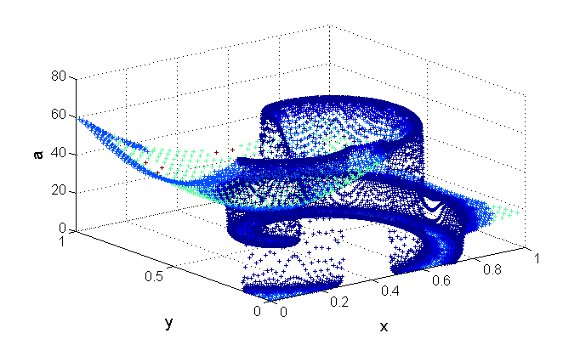
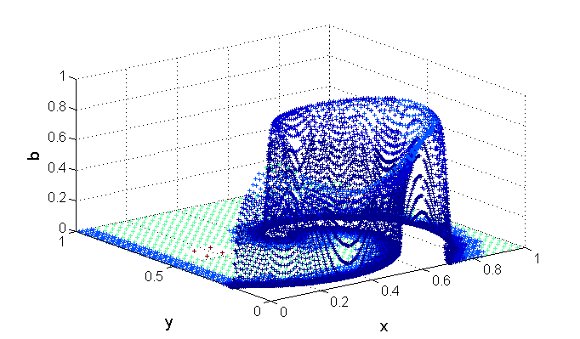
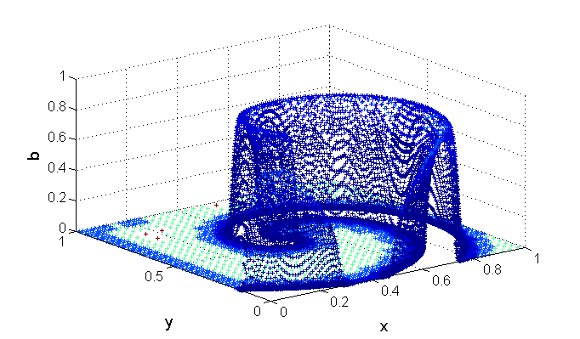
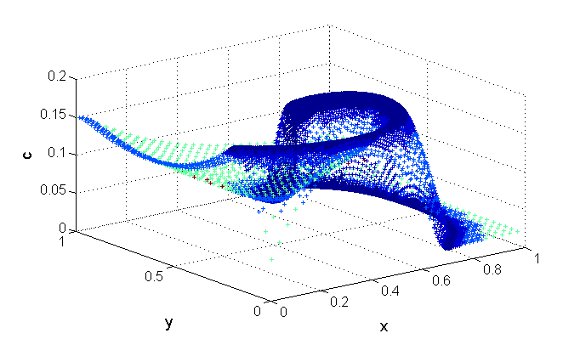
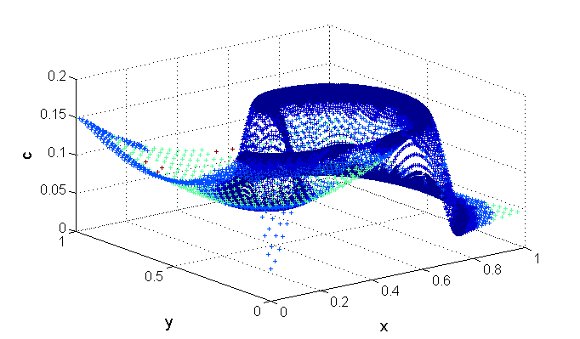
 at
at  (left) and
(left) and  (right). Variable
(right). Variable  (top),
(top),  (center) and
(center) and  (bottom), where the colors represent the grid levels. Finest grid:
(bottom), where the colors represent the grid levels. Finest grid: 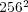
The reference or quasi-exact solution obtained with ROCK4 considers the coupled reaction-diffusion problem on a uniform mesh of 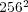 . The main limitation to perform such computation with Radau5 comes from its important memory requirements. Let us consider an application of the proposed MR/Splitting numerical strategy with
. The main limitation to perform such computation with Radau5 comes from its important memory requirements. Let us consider an application of the proposed MR/Splitting numerical strategy with  nested dyadic grids with
nested dyadic grids with 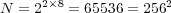 cells on the finest grid
cells on the finest grid 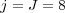 . The time integration method uses the RDR Strang
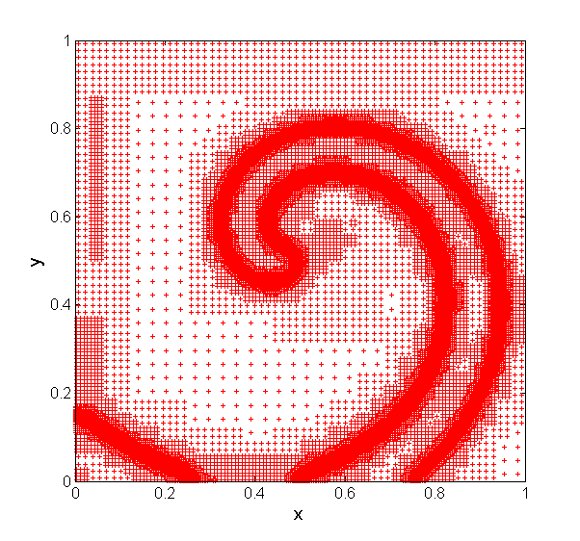
. The time integration method uses the RDR Strang 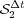 scheme with Radau5 for the time integration of the reaction term and ROCK4 for the diffusive part. The spiral waves simulated can be seen into Figure 2, where colors represent the grid levels at
scheme with Radau5 for the time integration of the reaction term and ROCK4 for the diffusive part. The spiral waves simulated can be seen into Figure 2, where colors represent the grid levels at 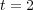 , when the wave is fully developed, and at
, when the wave is fully developed, and at  , after a complete rotation period: the adapted grids are tightened around the stiff regions and clearly propagate along the waves.
, after a complete rotation period: the adapted grids are tightened around the stiff regions and clearly propagate along the waves.
The splitting time step is set by the desired level of accuracy in the resolution of the wave speed, the wave profile, both, or any other parameter, depending on the problem and considering that each subsystem if perfectly resolved. It is thus only depending on the global phenomenon we want to describe and therefore, on the degree of decoupling we can achieve between the various subsystems within a prescribed error tolerance. For instance, in this particular application, we have chosen a splitting time step 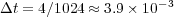 that guarantees a resolution of the wave speed with relative error lower than
that guarantees a resolution of the wave speed with relative error lower than 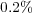 and normalized
and normalized 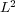 -error
-error 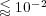 for all variables, comparing the splitting resolution with the quasi-exact reference one. For these propagating waves problems, a fixed splitting time step is more than reasonable to precisely describe the global coupling of the split phenomena.
for all variables, comparing the splitting resolution with the quasi-exact reference one. For these propagating waves problems, a fixed splitting time step is more than reasonable to precisely describe the global coupling of the split phenomena.
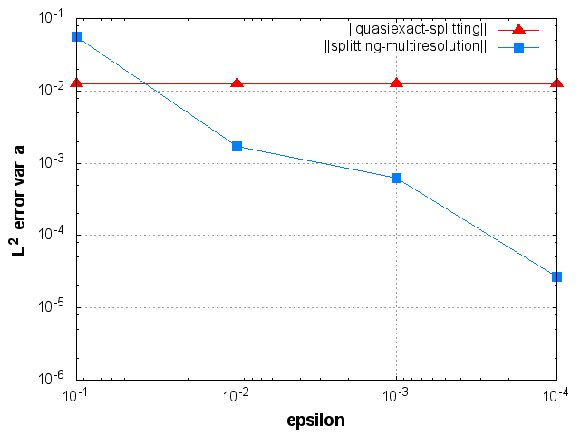
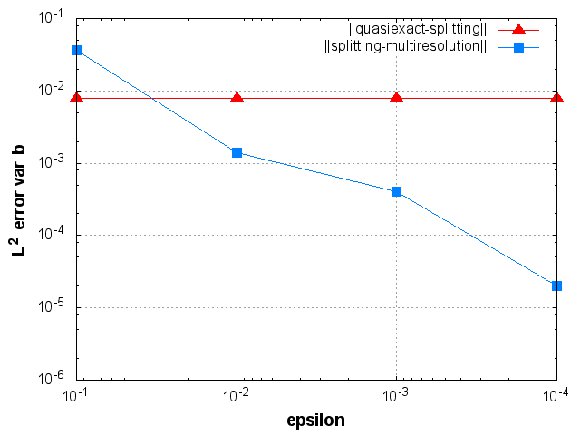
Considering now the 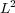 -error of the MR/Splitting results,
-error of the MR/Splitting results, 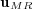 , with respect to the reference quasi-exact solution,
, with respect to the reference quasi-exact solution, 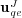 , we decompose it into two parts, the error coming from the splitting process and that of the multiresolution decomposition:
, we decompose it into two parts, the error coming from the splitting process and that of the multiresolution decomposition:
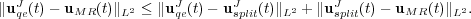 | (14) |
Therefore, we also consider the splitting solution 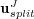 obtained without grid adaptation on the uniform finest grid
obtained without grid adaptation on the uniform finest grid 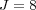 . Figure 3 shows these errors for variables
. Figure 3 shows these errors for variables  ,
,  and
and  , and for different threshold values
, and for different threshold values  at final time
at final time 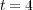 . The splitting error
. The splitting error 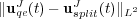 is computed on the finest grid and does not depend on the grid adaptation process: it is fixed by the splitting time step
is computed on the finest grid and does not depend on the grid adaptation process: it is fixed by the splitting time step 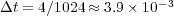 . The error coming from the multiresolution process is given by
. The error coming from the multiresolution process is given by 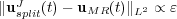 [11, 16], considering that both solutions use the same time integration strategy. In this case, these error estimates show that for
[11, 16], considering that both solutions use the same time integration strategy. In this case, these error estimates show that for 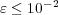 , the multiresolution errors become negligible compared to the operator splitting ones.
, the multiresolution errors become negligible compared to the operator splitting ones.
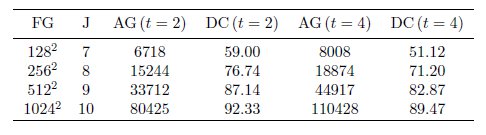
Nevertheless, this numerical strategy becomes really interesting on behalf of more accurate simulations of phenomena requiring very fine spatial resolution, for which standard strategies are simply unfeasible with conventional computing resources. Therefore, we study now the same problem but with finer spatial discretizations on the finest grid at 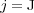 . Table 1 summarizes these results for the threshold value
. Table 1 summarizes these results for the threshold value 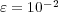 . The data compression (
. The data compression (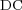 ) is defined as one minus the ratio between the number of cells on the adapted grid (
) is defined as one minus the ratio between the number of cells on the adapted grid (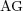 ) and those on the finest uniform grid (
) and those on the finest uniform grid (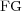 ), expressing the whole as a percentage:
), expressing the whole as a percentage:
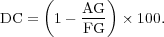 | (15) |
Data compression increases with the number of levels as the space scales present in the problem are better discriminated by finer spatial resolutions.
 ) and number of cells on the adapted grid (
) and number of cells on the adapted grid (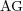 ) for
) for 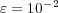 and different finest grids (
and different finest grids (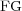 ) and levels of refinement (
) and levels of refinement (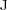 )
) 
In order to take into account the memory requirements of each resolution strategy for a fine spatial resolution of 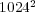 , we estimate the array size of the working space needed by Radau5 and ROCK4:
, we estimate the array size of the working space needed by Radau5 and ROCK4:
where 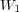 and
and 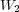 are the number of unknowns solved by Radau5 and ROCK4. In the case of an uniform mesh, the total number of unknowns is
are the number of unknowns solved by Radau5 and ROCK4. In the case of an uniform mesh, the total number of unknowns is 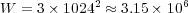 and thus, the global size
and thus, the global size 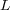 required for each solver is:
required for each solver is:
- Quasi-exact:
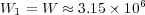 and
and 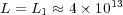 .
. - Splitting:
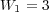 ,
, 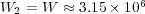 and
and 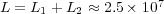 .
. - MR/Splitting with
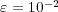 :
: 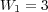 ,
, 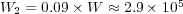 and
and 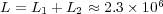 ; with average data compression of
; with average data compression of 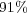 .
.
Considering a standard platform on which each double precision value is represented by 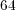 bits, each solver shall require
bits, each solver shall require 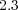 Pb,
Pb, 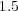 Gb and
Gb and 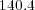 Mb.
Mb.
Therefore, on the one hand, it is hopeless trying to solve problem (13) with the quasi-exact strategy for these very fine discretizations, at least with standard computing resources. For instance, for these 2D simulations we have used an Intel(R) Core(TM)2 processor of 2 GHz with memory capacity of 2 GB. And on the other hand, also a splitting strategy becomes more difficult to implement since the diffusion term is solved considering the entire spatial domain at once. A major advantage of the proposed numerical strategy is the possibility of representing results in a highly compressed way. As an example, Figure 4 shows the adapted grids obtained for the 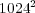 configuration with
configuration with 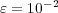 .
.
We consider problem (13), now in a 3D configuration with the same parameters considered in the 2D case for a time domain of ![[0,2]](/img/revistas/cleiej/v14n1/1a07205x.png) and in a space region of
and in a space region of ![[0,1]× [0,1]× [0,1]](/img/revistas/cleiej/v14n1/1a07206x.png) . The main goal of this part is to illustrate the feasibility of performing large simulation domains with standard computing resources; therefore, let us consider
. The main goal of this part is to illustrate the feasibility of performing large simulation domains with standard computing resources; therefore, let us consider  nested dyadic grids with
nested dyadic grids with 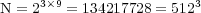 cells on the finest grid
cells on the finest grid 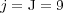 . For these 3D implementations, we used an AMD-Shanghai processor of 2.7 GHz with memory capacity of 32 GB. Then, with a threshold value of
. For these 3D implementations, we used an AMD-Shanghai processor of 2.7 GHz with memory capacity of 32 GB. Then, with a threshold value of 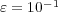 and a splitting time step
and a splitting time step 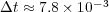 , the implementation of the proposed numerical strategy features data compressions that goes from
, the implementation of the proposed numerical strategy features data compressions that goes from 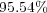 for the initial condition,
for the initial condition, 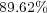 at
at  when the scroll waves are fully developed and
when the scroll waves are fully developed and 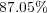 at final time
at final time  .
.
For this configuration, smaller threshold values yield larger simulation domains which are not longer feasible with the considered computing resource and the current state of development of the code. Figure 5 shows the evolution of the finest grid of the adapted grid during the period of study. We distinguish clearly the development of the scroll wave where colors represent the values of variable  : the finest regions correspond to the neighborhood of the wavefront.
: the finest regions correspond to the neighborhood of the wavefront.
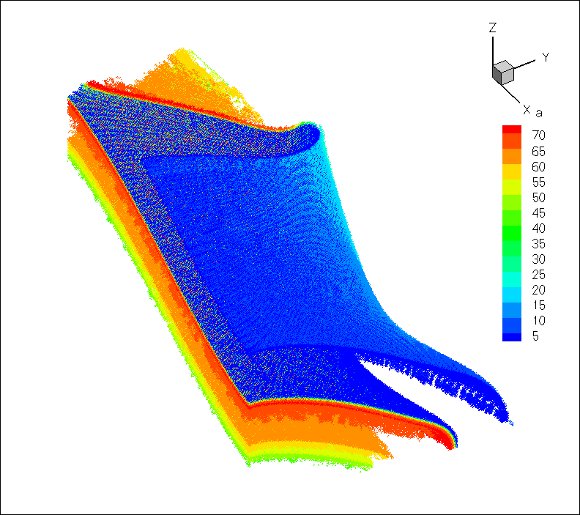
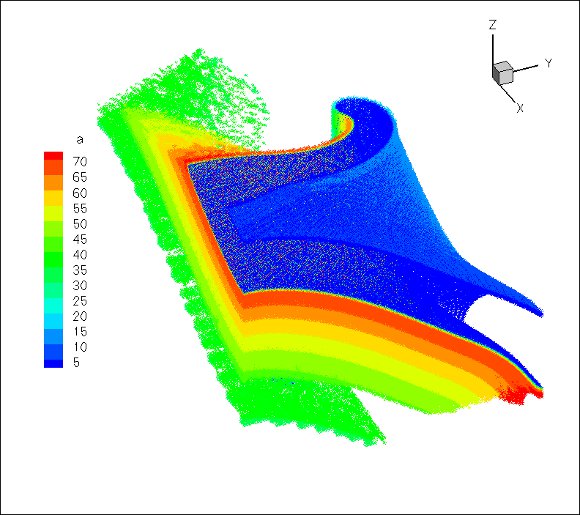
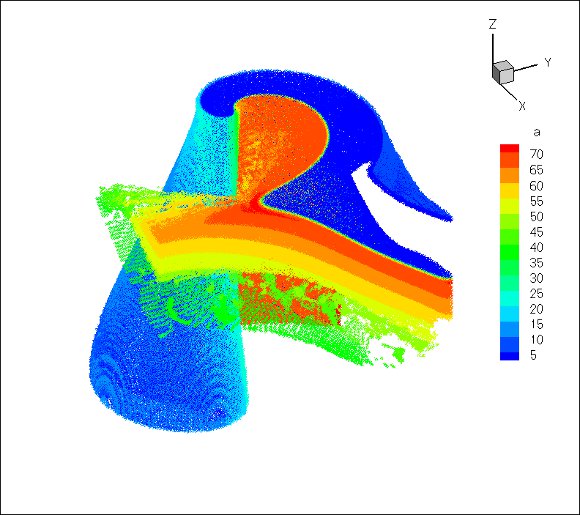
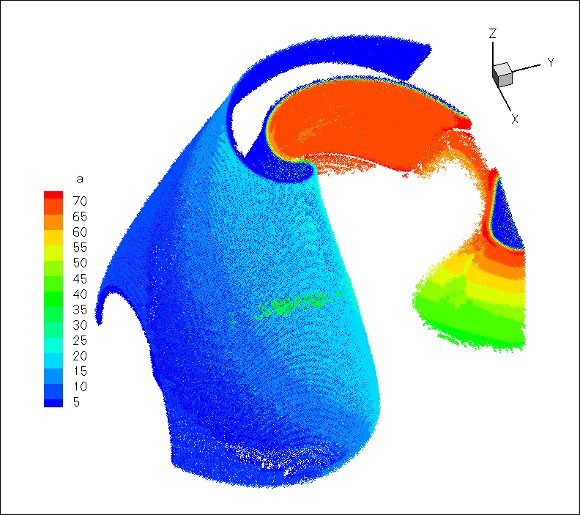
 (top left),
(top left),  (top right),
(top right), 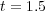 (bottom left) and
(bottom left) and  (bottom right).
(bottom right). 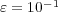 , where colors represent values of variable
, where colors represent values of variable  . Finest grid:
. Finest grid: 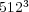
Performing the same comparison concerning memory requirements, the total number of unknowns for this case is 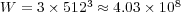 and the global size of
and the global size of 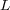 required by each solver is:
required by each solver is:
- Quasi-exact:
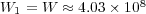 and
and 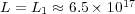 .
. - Splitting:
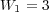 ,
, 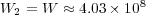 and
and 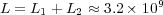 .
. - MR/Splitting with
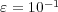 :
: 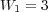 ,
, 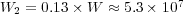 and
and 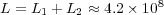 ; with a data compression of
; with a data compression of 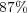 .
.
Therefore, each solver shall require at least 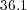 Eb,
Eb, 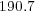 Gb and
Gb and 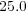 Gb of memory capacity.
Gb of memory capacity.
The present work proposes a simple and solid numerical strategy that couples adaptive multiresolution techniques with a new operator splitting strategy for multi-scale reactions waves modeled by stiff reaction-diffusion systems. The splitting time step is chosen on the sole basis of the structure of the continuous system and its decoupling capabilities, but not related to any stability requirement of the numerical methods involved in order to integrate each subsystem, even if strong stiffness is present. The technique considers, on the one hand, dedicated high order time integration methods to properly solve the entire spectrum of temporal scales of both the reaction and the diffusion part; and on the other hand, an adaptive multiresolution technique to represent and treat more accurately local spatial gradients associated with the wave front. The global accuracy of the simulation is mainly settled by the splitting time step which is evaluated based on theoretical and numerical results in the context of self-similar propagating waves. The resulting highly compressed data representations as well as the accurate and feasible resolution of these stiff phenomena prove that large computational domains previously out of reach can be successfully simulated with conventional computing resources.
We have focused our attention on reaction-diffusion systems in order to settle the foundations for simulation of more complex phenomena with fully convection-reaction-diffusion systems or more detailed models. In particular, we search to extend this strategy to multi-scale problems in combustion domain, where other numerical techniques have already been proposed (see for instance [21, 22]) and where there is a continuous research of new and more efficient methods. Therefore, an important amount of work is still in progress concerning on the one hand, programming features such as data structures, optimized routines and parallelization strategies. And on the other hand, numerical analysis of theoretical aspects, which may surely allow the introduction of dynamical error estimators and even adaptive splitting time steps for more general multi-scale phenomena [23, 24]; these are particular topics of our current research.
This research was supported by a fundamental project grant from ANR (French National Research Agency - ANR Blancs) Séchelles (project leader S. Descombes) and by a CNRS PEPS Maths-ST2I project MIPAC (project leader V. Louvet). M. Duarte has a Ph.D. grant from Mathematics (INSMI) and Engineering (INSIS) Institutes of CNRS and supported by INCA project (National Initiative for Advanced Combustion).
[1] Y. D’Angelo. Analyse et Simulation Numérique de Phénomènes liés à la Combustion Supersonique. PhD thesis, Ecole Nationale des Ponts et Chaussées, 1994.
[2] J. G. Verwer, B. P. Sommeijer, and W. Hundsdorfer. RKC time-stepping for advection-diffusion-reaction problems. J. Comput. Phys., 201(1):61–79, 2004.
[3] L. F. Shampine, B. P. Sommeijer, and J. G. Verwer. IRKC: An IMEX solver for stiff diffusion-reaction PDEs. J. Comput. Appl. Math., 196(2):485–497, 2006.
[4] J. G. Verwer and B. Sportisse. Note on operator splitting in a stiff linear case. Rep. MAS-R9830, 1998.
[5] B. Sportisse. An analysis of operator splitting techniques in the stiff case. J. Comput. Phys., 161(1):140–168, 2000.
[6] S. Descombes and M. Massot. Operator splitting for nonlinear reaction-diffusion systems with an entropic structure: Singular perturbation and order reduction. Numer. Math., 97(4):667–698, 2004.
[7] S. Descombes, T. Dumont, V. Louvet, M. Massot, F. Laurent, and J. Beaulaurier. Operator splitting techniques for multi-scale reacting waves and application to Low Mach number flames with complex chemistry: Theoretical and numerical aspects. In preparation, 2011.
[8] S. Descombes, T. Dumont, V. Louvet, and M. Massot. On the local and global errors of splitting approximations of reaction-diffusion equations with high spatial gradients. Int. J. of Computer Mathematics, 84(6):749–765, 2007.
[9] E. Hairer and G. Wanner. Solving ordinary differential equations II. Springer-Verlag, Berlin, second edition, 1996. Stiff and differential-algebraic problems.
[10] A. Abdulle. Fourth order Chebyshev methods with recurrence relation. SIAM J. Sci. Comput., 23:2041–2054, 2002.
[11] A. Harten. Multiresolution algorithms for the numerical solution of hyperbolic conservation laws. Comm. Pure and Applied Math., 48:1305–1342, 1995.
[12] A. Cohen. Wavelet methods in numerical analysis, volume 7. Elsevier, Amsterdam, 2000.
[13] S. Müller. Adaptive multiscale schemes for conservation laws, volume 27. Springer-Verlag, Heidelberg, 2003.
[14] G. Strang. On the construction and comparison of difference schemes. SIAM J. Numer. Anal., 5:506–517, 1968.
[15] T. Dumont, M. Duarte, S. Descombes, M.A. Dronne, M. Massot, and V. Louvet. Simulation of human ischemic stroke in realistic 3D geometry: A numerical strategy. Submitted to Bulletin of Math. Biology, available on HAL (http://hal.archives-ouvertes.fr/hal-00546223), 2010.
[16] A. Cohen, S.M. Kaber, S. Müller, and M. Postel. Fully adaptive multiresolution finite volume schemes for conservation laws. Math. of Comp., 72:183–225, 2003.
[17] I.R. Epstein and J.A. Pojman. An Introduction to Nonlinear Chemical Dynamics. Oxford University Press, 1998. Oscillations, Waves, Patterns and Chaos.
[18] P. Gray and S. K. Scott. Chemical oscillations and instabilites. Oxford University Press, 1994.
[19] W. Heineken and G. Warnecke. Partitioning methods for reaction-diffusion problems. Applied Numerical Mathematics, 56(7):981–1000, 2006.
[20] S. Descombes, T. Dumont, and M. Massot. Operator splitting for stiff nonlinear reaction-diffusion systems: Order reduction and application to spiral waves. In Patterns and waves, pages 386–482. AkademPrint, St. Petersburg, 2003.
[21] M. S. Day and J. B. Bell. Numerical simulation of laminar reacting flows with complex chemistry. Combust. Theory Modelling, 4:535–556, 2000.
[22] H. N. Najm and O. M. Knio. Modeling Low Mach number reacting flow with detailed chemistry and transport. Journal of Scientific Computing, 25(1/2):263–287, 2005.
[23] S. Descombes, M. Duarte, T. Dumont, V. Louvet, and M. Massot. Adaptive time splitting method for multi-scale evolutionary PDEs. Confluentes Mathematici (to appear), available on HAL (http://hal.archives-ouvertes.fr/hal-00587036), 2011.
[24] M. Duarte, Z. Bonaventura, M. Massot, A. Bourdon, S. Descombes, and T. Dumont. A new numerical strategy with space-time adaptivity and error control for multi-scale gas discharge simulations. Submitted to J. of Comp. Physics, available on HAL (http://hal.archives-ouvertes.fr/hal-00573043), 2011.












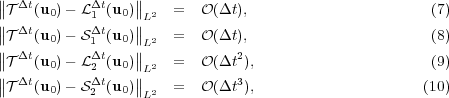
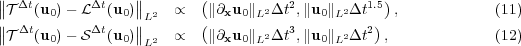
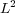 errors at
errors at  . Variable
. Variable  (top left),
(top left),  (top right) and
(top right) and  (bottom). Finest grid:
(bottom). Finest grid: 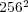
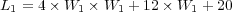 (from
(from 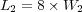 (from
(from 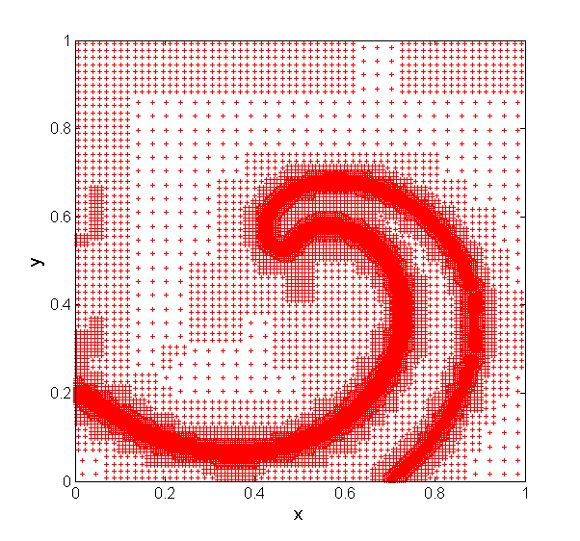
 (left) and
(left) and  (right),
(right),  . Finest grid:
. Finest grid: