Servicios Personalizados
Revista
Articulo
Links relacionados
Compartir
Ciencias Psicológicas
versión On-line ISSN 1688-4221
Cienc. Psicol. vol.15 no.1 Montevideo jun. 2021 Epub 01-Jun-2021
https://doi.org/10.22235/cp.v15i1.2170
Original Articles
Attitude towards mathematics of fifth grade primary school students and self-efficacy of teachers
1 Universitat Rovira i Virgili, España jaimerodrigo.segarra@urv.cat
In this research work, the attitude towards mathematics of 194 fifth grade students is studied. Additionally, the arithmetic mean between teachers' beliefs about mathematics teaching and students' attitudes is studied. The Mathematics Attitude Scale (MAS) is used to measure students' attitudes. The Mathematics Teaching Efficacy Belief Instrument (Mtebi) is used to measure the teachers' efficacy beliefs. The results indicate that students have a favorable level of attitude towards mathematics. The confidence factor has higher scores. The study of means indicates that students with a higher attitude have mathematics teachers with greater teachers' self-efficacy in teaching mathematics. Teachers should consider attitude as an important factor in student cognitive development.
Keywords: attitude; self-efficacy; mathematics; primary education
En este trabajo se estudia la actitud hacia las matemáticas de 194 estudiantes de quinto grado. Adicionalmente, se estudia las medias aritméticas entre las creencias de la enseñanza de las matemáticas de los profesores y la actitud de los estudiantes. Se utiliza la Escala de Actitud hacia las Matemáticas (EAM) para medir la actitud de los estudiantes. El Instrumento de Creencias de Eficacia en la Enseñanza de Matemáticas (Mtebi, por su sigla en inglés) se utiliza para medir las creencias de eficacia de los profesores. Los resultados indican que los estudiantes tienen una actitud positiva hacia las matemáticas. El factor confianza tiene puntuaciones más altas. El estudio de las medias indica que los estudiantes con mayor actitud positiva tienen profesores de matemáticas con mayor autoeficacia de la enseñanza de las matemáticas. Los profesores deben considerar a la actitud como un factor importante en el desarrollo cognitivo del estudiante.
Palabras clave: actitud; autoeficacia; matemáticas; educación primaria
Nesta investigação se estuda a atitude em relação à matemática de 194 alunos do quinto ano. Adicionalmente, são estudadas as médias aritméticas entre as crenças do ensino de matemática dos professores e a atitude dos alunos. A Escala de Atitude em relação à Matemática (EAM) é usada para medir a atitude dos alunos. O Instrumento de Crenças de Eficácia do Ensino de Matemática (Mtebi, por sua sigla em inglês) é usado para medir as crenças de eficácia dos professores. Os resultados indicam que os alunos apresentam uma atitude positiva em relação à matemática. O fator confiança tem pontuações mais altas. O estudo das médias indica que os alunos com atitude mais positiva possuem professores de matemática com maior autoeficácia no ensino de matemática. Os professores devem considerar a atitude como um fator importante no desenvolvimento cognitivo do aluno.
Palavras-chave: atitude; autoeficácia; matemática; educação primária
Learning math became a challenge for most of the students. Lack of motivation or learning difficulty causes many students to say “I am not good at math” before they even try to solve math problems. This general problem is considered a matter of attitudes towards mathematics rather than the lack of skills (Colomeischi & Colomeischi, 2015). Bausela (2018) also indicated that a large number of schoolchildren experience difficulties in mathematics.
Some researchers emphasized the importance of studying students' attitude towards mathematics (e.g., Aiken, 1970; Auzmendi, 1992; Hourigan & Leavy, 2019; Ursini & Sánchez, 2008). It is recognized that the role of motivation and emotions is crucial for learning (Kim, Park & Cozart, 2014). When students lack motivation, their learning process rarely begins, and when students feel desperate, their learning process is easily interrupted (Bandura, 1986; Schunk, 1991).
Besides, Aiken (1970) indicated that attitude is a disposition or tendency learned by an individual to respond positively or negatively to some object, situation, concept or another person. Neale (1969) also defined attitude towards mathematics as an aggregate measure of the likes or dislikes of mathematics, a tendency to participate in or avoid mathematical activities, the belief that one is good or bad at mathematics, and the belief that mathematics math is useful or useless.
Several researchers indicated that students should have a positive attitude towards mathematics, since it influences their academic performance in mathematics (e.g., Bazán, Espinosa & Farro, 2001; Figueroa et al., 2012; Salaya, 2006). However, some researchers showed that students at all levels of education often have negative attitudes towards mathematics (e.g., Boaler, 1997; Michaluk, Stoiko, Stewart, & Stewart, 2018). However, it is important that students have positive attitudes towards mathematics, since attitudes affect their academic performance and behavior (Cueto, Andrade & León, 2003).
Moreover, in the belief construct, Bandura (1977) indicated that the belief that people have are their own abilities to carry out appropriate behaviors, in a way that allows them to successfully achieve a goal. A person's self-efficacy can influence the effort they make in a given situation and how long they persist in a given task (Goddard, Hoy, & Woolfolk, 2004). Expectations determine how much effort people will expend and how long they will persist to face obstacles and aversive experiences. The stronger the perceived self-efficacy, the more active the efforts will be.
Taking into account Bandura's theory (1977; 1997), studies of teachers' efficacy beliefs have been based on two separate dimensions (Hassan & Hassan, 2012). The first dimension, teaching self-efficacy, represents a teacher's belief in their abilities and capabilities to be an effective teacher. The second dimension, the expectation of teaching outcomes, is a teacher's belief that effective teaching can achieve good student learning, regardless of external factors such as family environment, family background, and the influence of parents (Swars, Hart, Smith, Smith and Tolar, 2007).
Several researchers have studied the attitude towards mathematics of students (e.g., Recber, Isiksal, & Koç, 2018; Shahid & Ullah, 2008). Besides, other researchers studied the influence of teachers' beliefs on students' attitudes (e.g., Chang, 2015).
Nicolaidou and Philippou (2003) studied the relationships between students' attitudes towards mathematics, self-efficacy beliefs, and problem solving (academic achievement). In a sample of 238 fifth-grade students, the authors found that there is a significant relationship between attitudes and academic achievement; and a stronger relationship between efficacy and academic achievement. Attitudes and efficacy were also correlated and both predicted academic achievement in problem solving. However, efficacy was a more powerful predictor than attitudes.
Shahid and Ullah (2008) with a sample of 685 tenth-year high school students applied the mathematical attitude scale of Fennema and Sherman (1976). The authors indicated that the success of students in mathematics depends on the attitude towards mathematics. They also indicated that attitude influences students' participation rate in math class.
Mohamed and Waheed (2011) studied the attitude towards mathematics. A total of 200 high school students were administered a questionnaire to find out their attitudes towards mathematics, the students answered questions about their personal confidence in mathematics and the perceived usefulness of mathematics. The authors founded that attitude is a factor that influences students' academic achievement in mathematics. Additionally, the results show that students have a positive attitude towards mathematics.
Chang (2015) examined the relationships between the efficacy beliefs of fifth grade teachers with the self-efficacy and mathematical performance of their students. Using a sample of 1,244 students and 58 teachers, the authors found that the efficacy beliefs of mathematics teachers have a significant influence on students' self-efficacy and academic achievement in mathematics.
Attitude towards mathematics is a construct that plays an important role in mathematics education (Zan & Di Martino, 2007). Besides, Charalambous, Philippou and Kyriakides (2008) emphasized the importance of studying the construct of beliefs about the efficacy of mathematics teaching since it is related to the academic performance of students. In this context, this research focuses on the study of the attitude towards mathematics of fifth grade students in Primary Education. Additionally, the means between the attitude towards mathematics of fifth grade students and the belief in the self-efficacy of mathematics teaching held by mathematics teachers are studied. Unlike other studies, this paper will study five factors of the attitude of mathematics and the beliefs of the efficacy of teaching mathematics.
We defined three questions to fulfill the purpose of the investigation:
-What is the level of the attitude towards mathematics of the fifth-grade students of primary education?
-Are there significant differences between the five factors of the attitude towards mathematics of students in the fifth grade of primary education?
-Is there a correspondence between the high means of the mathematics teaching efficacy belief and the attitude towards mathematics of the fifth-grade students?
Method
Participants
The participants in this study corresponded to fifth-grade students from five primary education in the city of Tarragona, Spain, in the academic period 2019-2020. Participation was voluntary and anonymous. The sample of this study corresponds to n = 194. The students are in the fifth grade (approximately 9 to 11 years old). Besides, there is a sample of grade level teachers (classroom) to whom the test was applied, specifically there are 8 teachers (mathematics) of the 5th grade of primary education.
Instruments
For this research, we used two instruments: 1) the Attitude towards Mathematics Scale (AMS) by Auzmendi (1992) was applied to fifth grade students; 2) the Mathematics Teaching Efficacy Belief Instrument (Mtebi) for teachers (Enochs, Smith & Huinker, 2000), was applied to mathematics teachers.
The Attitude towards Mathematics Scale (AMS) allows a comprehensive analysis of the attitude towards mathematics for students, collecting the most significant factors for its study (Auzmendi, 1992). The AMS consists of 25 items on a five-point Likert scale that measures from one (totally disagree) to five (totally agree). As in the Mtebi, the third element of the Likert scale, which was in the original version of the AMS, was eliminated. The AMS establishes five factors: liking (4, 9, 14 and 24), anxiety (2, 3, 7, 8, 12, 13, 17, 18 and 22), motivation (5, 10 and 25), utility (1, 6, 15, 16, 19 and 21) and confidence (11, 20 and 23). Ten of the items on the AMS have an inverse score (2, 5, 7, 10, 12, 15, 16, 17, 22 and 25). Responses to these items should be inverted before being added to the total AMS score. To obtain the partial result for each factor, the scores obtained in the corresponding items are added.
The Stebi (adapted Mtebi) has two forms: for teachers in training and for teachers in service (Enochs & Riggs, 1990). In this research, the Mtebi was adapted for in-service teachers, the questions were reformulated in the present tense. Several researchers used the MTEBI in in-service teachers (e.g., Liu, Jack, & Chiu, 2007; Segarra & Julià, 2020; Swars, Daane & Giesen, 2006; Takunyaci, & Takunyaci, 2014). The Mtebi consists of 21 questions on a five-point Likert scale that measures from one (totally disagree) to five (totally agree). As in (Liu et al., 2007; Segarra & Julià, 2020), the third element of the Likert scale, which was in the original version of MTEBI, was removed to encourage teachers to indicate a level of certainty. The MTEBI is made up of two subscales. The first is the Personal Mathematics Teaching Efficacy or Teaching Self-Efficacy (PMTE) subscale, which is made up of 13 items (2, 3, 5, 6, 8, 11, 15, 16, 17, 18, 19, 20 and 21). The other subscale is the Mathematics Instructional Outcome Expectation (MTOE), which is made up of 8 items (1, 4, 7, 9, 10, 12, 13, and 14). Eight of the PMTE items have an inverse score (3, 6, 8, 15, 17, 18, 19 and 21). Responses for these items should be reversed before being added to the total PMTE score.
Procedure
The two instruments Mtebi and AMS were delivered to the directors of each educational institution. Subsequently, the principal was in charge of passing the mathematics teaching effectiveness beliefs test (Mtebi) to the mathematics teachers in each classroom, in this test the teachers had 20 minutes to answer the 21 questions. The attitude towards mathematics test (AMS) was delivered to each classroom tutor, so that after the respective authorization of the legal representatives, the test could be applied. They had 40 minutes to answer the 25 questions. For the application of the AMS, the respective accompaniment to the tutors was carried out in order to guarantee the control of the application of the instrument.
Data analysis
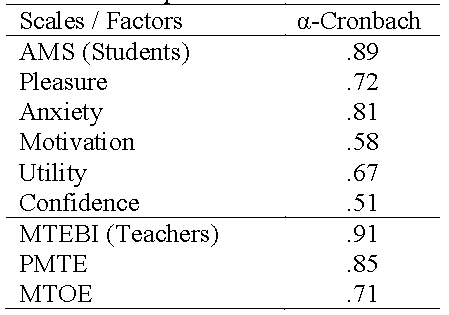
This research is a quantitative study. To determine the reliability of the results obtained, the internal consistency of the scales was analyzed with Cronbach's alpha test (Cronbach, 1951). Table 1 shows the Cronbach's alpha coefficients of the AMS and its five factors (liking, anxiety, motivation, usefulness and confidence). In addition, Table 1 shows the Cronbach's alpha coefficients for the Mtebi and its two subscales (PMTE and MOTE). George and Mallery (2003) provided the following general rules for Cronbach's alpha (α> 0.9 - Excellent; α> 0.8 - Good; α> 0.7 - Fair; α> 0.6 - Questionable; α> 0.5 - Poor; and α <0.5 - Unacceptable). In the case of the motivation and confidence factors, the Cronbach's alpha value is bad, this fact is caused because these two factors are less differentiated and specific (Auzmendi, 1992). In addition, it must be considered that both scales are composed of three items and that the internal consistency found through the Cronbach's α method tends to be lower if the number of items in an instrument is reduced (Auzmendi, 1992). It is important to note that Cronbach's alpha for the total AMS is good and for the total Mtebi it is excellent.
All descriptive and inferential statistics calculations were performed using the R programming language. Graphics were generated in R Studio and Microsoft Excel.
Results
Question 1. What is the level of the attitude towards mathematics of the fifth grade students of Primary Education?
This section studies the results of the AMS and each of the five factors. To measure the AMS and its factors, it is essential that when assigning the numerical scores to the answers, it is taken into account whether the statement is in a positive or negative sense. Table 2 shows the criteria used to classify these variables as positive and negative. To perform the criteria in Table 2, the reference by Ursini and Sánchez (2019) was analyzed.
The results indicate that the arithmetic mean of the attitude towards mathematics is 3.07. Considering the values in Table 2, we can affirm that the attitude towards mathematics is positive in 86 % of the fifth-grade students of primary education. However, 14 % of the participants have a negative attitude towards mathematics. Next, the arithmetic mean scores of each of the AMS factors are studied.
Pleasure factor. Table 3 shows the scores of the arithmetic means and standard deviations obtained in the four questions of the pleasure factor. In this factor, students obtain a mean score of 2.64 (SD = .77). 54 % of students have a positive liking for mathematics. However, it must be considered that a large percentage have negative liking towards mathematics (46 %). The arithmetic mean score obtained in this factor is lower than the arithmetic mean scores obtained in the AMS (2.64 <3.07). Note that the highest score is question 14 with a mean of 2.96. On the other hand, question 9 obtains the lowest score of the mean of 2.22.
Anxiety factor. Table 4 shows the arithmetic mean scores and standard deviations obtained for each anxiety factor question. In this factor, students obtain a mean score of 3.08 (SD = .63). The value of the mean score corresponding to the anxiety factor is higher than the arithmetic mean score for the attitude towards mathematics (3.08 > 3.07). In this factor, it should be taken into account that the scale is coded so that the higher the score, the lower the anxiety (Flores & Auzmendi, 2015). Considering the mean and the type of coding of this scale, it can be said that the students have a low level of anxiety. It is important to highlight that question 18 has a lower score with an arithmetic mean of 2.82; question 22 has a higher score (M = 3.27).
Utility factor. Table 5 shows the arithmetic mean scores corresponding to each of the utility factor questions. The mean score for this factor is 3.01 (SD = .58). The value of the mean score of this factor is lower than the arithmetic mean score of the AMS (3.01 <3.07). Considering Table 2, we can affirm that the students responded in a positive sense about the utility. In this factor, the highest score (M = 3.40) was obtained in question 6 and the lowest score (M = 2.52) in question 19. Table 5 shows that, in all the questions, the students give an answer in positive sense.
Motivation factor. Table 6 shows the arithmetic mean scores and the standard deviations of the scores given for the motivation factor questions, with a mean score of 3.18 (SD = 0.70). The arithmetic mean score of this factor is higher than the arithmetic mean score of the AMS (3.18 > 3.07). 79 % of students responded positively to the motivational factor questions. In this factor, the highest score of the arithmetic mean is in question 25, followed by question 5, and the question with the lowest score is 10. Table 6 shows that, in all the questions, the students give a positive answer.
Confidence factor. Table 7 shows the values of the arithmetic mean scores corresponding to the questions of the confidence factor. The average score obtained by the students in this is 3.44 (SD = .55). The value of the score of the mean of this factor is higher than the score of the arithmetic mean of the AMS (3.44 > 3.07). Besides, 79 % of the students answered the questions of this factor in a positive sense. Question 23 has the highest score, followed by question 11. Finally, there is question 20 with a lower arithmetic mean score. Table 7 shows that, in the three questions, the students give an answer in the positive sense.
Question 2. Are there significant differences between the five factors in fifth-grade students' attitude toward mathematics?
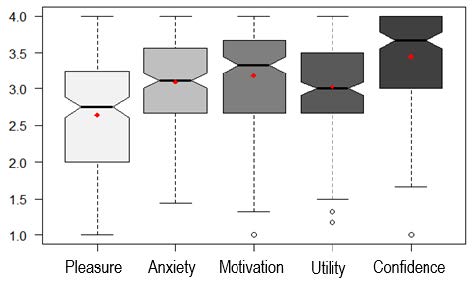
To carry out the study, the total score of the questions for each factor obtained by each participant was calculated (the total score is averaged by the number of items rated by the participant). To study the distribution of the scores, Figure 1 shows the arithmetic mean scores of the five factors corresponding to fifth grade students. Specifically, the boxplot allows you to identify the quartiles, the median (represented by horizontal lines in thinner regions), and the mean (denoted by dots).
Figure 1 shows that the range of values of the liking factor is clearly wider than the other four groups. Specifically, the minimum value of the liking factor is the smallest (1). In the case of the anxiety factor, the number of small values is below 1.5. In the case of the motivation, utility and trust factors, there are outliers lower than 1.5. Additionally, it shows that the pleasure factor has a lower score in the arithmetic mean.
Moreover, to verify if the differences between arithmetic means are statistically significant. Compliance with the normality hypothesis conditions (Shapiro-Wilk) and homoscedasticity (Bartlett) (p-value> .05) is verified. According to the data conditions, the Anova test is applied. The Anova result indicates that there are significant differences between the arithmetic means of the five groups (F = 41.89, p = 1.66 × 10-32). Subsequently, a post-hoc analysis is applied to study the significant differences between each pair of groups. Specifically, Tukey's HSD test (honestly significant difference) is applied. Table 8 shows the p-values, which allow us to conclude that the difference between the calculated arithmetic mean scores is statistically significant between most pairs of the AMS factors. Among the even factors with no significant differences are: anxiety and motivation (p = .68); anxiety and utility (p = .73); and, finally, motivation and utility (p = .079).
Question 3. Is there a correspondence between the high means of the mathematics teaching efficacy belief and the attitude towards mathematics of the fifth-grade students?
Table 9 shows the arithmetic means and standard deviations of the scores obtained by the fifth-grade teachers. Considering the values in Table 2, the teachers give an affirmation in the positive sense to the questions of the PMTE and MTOE subscale.
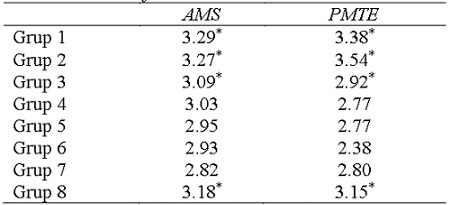
Table 10 shows the arithmetic means of the scores obtained by the fifth-grade teachers of primary education in the self-efficacy of mathematics teaching (PMTE). In addition, Table 10 shows the arithmetic means of the scores obtained by the fifth-grade students in the attitude towards mathematics. Specifically, Table 10 shows the means of the eight groups studied.
To determine which groups of students and teachers obtain different scores in attitude and self-efficacy, respectively, the t-Student test and Anova are applied. On the other hand, to determine which groups have higher scores, Tukey's HSD test is applied. Therefore, it can be said that the teachers of group 1, 2, 3 and 8 have a significantly higher mean (p <.05) than the other groups in the PMTE. Similarly, students in groups 1, 2, 3 and 8 have a significantly higher mean (p <.05) than the other groups in attitude towards mathematics. It can be verified that the groups coincide, the students with greater attitude have teachers with greater self-efficacy.
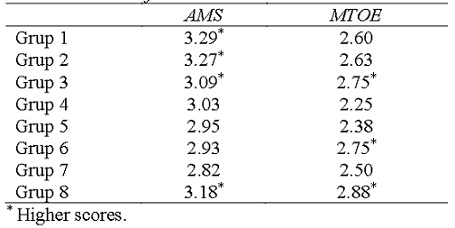
Table 11 shows the arithmetic means of the scores obtained by the mathematics teachers of the fifth grade of primary education in the expectation of results (MTOE). In addition, Table 11 shows the arithmetic means of the scores obtained by the fifth grade students in the attitude towards mathematics.
To determine which groups of students and teachers obtain different scores, the Student's t test and Anova are applied. In addition, to determine which groups have higher scores, Tukey's HSD test is applied. Therefore, it can be said that the teachers of group 3, 6 and 8 have a significantly higher mean (p <.05) than the other groups in the MTOE. Besides, students in group 1, 2, 3 and 8 have a significantly higher mean (p <.05) than the other groups in attitude towards mathematics. It can be verified that, unlike in the PMTE, the groups do not coincide. Therefore, it cannot be said that students with a higher attitude have teachers with a higher expectation of results.
Discussion
The purpose of this research was to study the attitude towards mathematics of fifth grade students of primary education. Additionally, the arithmetic means between the attitude towards mathematics of the students and the mathematics teaching efficacy belief of the fifth-grade mathematics teachers was studied.
To answer the first research question, the arithmetic mean scores of each question of the AMS factors for the group of participants were studied. The results indicated that students have a positive attitude towards mathematics. We agree with Tezer and Karasel (2010) who determined that one must have positive attitudes towards mathematics in order to have a good academic performance. Moreover, analyzing each of the factors, the students have a positive liking for mathematics. The results indicated that in the questions of the factor Pleasure they obtain lower scores than the other factors. The lowest score is on question 9 (I have fun talking to others about math). It is important that a high level is obtained in the pleasure factor since people who come to enjoy mathematics increase their intrinsic motivation and improve their learning (Ma & Kishor, 1997). In this study it can be said that the participants have a low level of anxiety. Anxiety is a facilitating variable of academic performance since moderate levels of it will produce, in the student body, a state of alertness or attention that will improve their performance (García, Martínez & Inglés, 2013). Students were found to be positively motivated towards mathematics. We agree, with the research by Flores and Auzmendi (2018), the participants obtain high scores in motivation. Also, in the utility factor it can be said that the students in all the questions respond in a positive sense. Finally, also, in the confidence factor, scores are obtained in a positive sense. This factor is important since mistrust in the use of mathematical concepts and procedures in solving mathematical situations for life, prevents good academic performance (Cardoso et al., 2012).
In the second research question, it was determined that students obtain higher scores in the confidence factor compared to the other factors. Besides, it is evident that in the pleasure factor, students obtain the lowest mean. Additionally, it was determined that there were no significant differences between the anxiety, utility and motivation factors, but it could be determined that these factors obtained higher mean scores than in the pleasure factor and lower mean scores than in the trust factor. It is important to point out that it is necessary to implement methodological strategies, in order to increase the pleasure towards mathematics.
In the last research question, it was determined that the groups of students that obtain a higher arithmetic mean in attitude towards mathematics have mathematics teachers with greater self-efficacy in teaching mathematics. That is, the self-efficacy of teachers influences the attitude towards mathematics of students. Besides, this relationship is not observed in the results expectation subscale (MTOE). In addition, it should be considered that teacher self-efficacy plays an important role in promoting students' academic achievement and their development of self-efficacy in the classroom, teachers should make efforts to establish a positive and collaborative work environment and learning in the service that promotes mathematics and education (Chang, 2015). Considering these important aspects of the self-efficacy of mathematics teaching, several authors have indicated the importance of providing better teacher preparation programs to develop their self-efficacy (e.g., Incikabi, 2013; Sancar, 2013).
Therefore, it would be very useful to include an assessment of students' attitude towards mathematics at the beginning of an academic period. Ideally, you should provide students with activities and experiences to improve the factors that score the lowest. Therefore, the educational authorities must consider as an important aspect the self-efficacy of the teaching of the teachers since this subscale influences the attitude of the students. It is evident that a low self-efficacy of the teacher can negatively influence the attitude of students, and this in turn, influences their academic performance.
Future research will study the relationship between fifth grade students' attitude towards mathematics and academic achievement; the self-efficacy of teachers and the academic achievement of students; teachers 'self-efficacy, students' attitude and academic achievement (to study the best predictor of academic achievement).
REFERENCES
Aiken, L. (1970). Attitudes towards mathematics. Review of Educational Research, 40, 551-596. doi: 10.3102/00346543040004551 [ Links ]
Auzmendi, E. (1992). Las actitudes hacia la matemática-estadística en las enseñanzas media y universitaria. En Características y medición. España: Mensajero. [ Links ]
Bandura, A. (1977). Self-efficacy: Toward a unifying theory of behavioral change. Psychological review, 84(2), 191-215. doi: 10.1037/0033-295X.84.2.191 [ Links ]
Bandura, A. (1986). Social foundations of thought and action: A social cognitivetheory. Englewood Cliffs: Prentice Hall. [ Links ]
Bandura, A. (1997). Self-efficacy: The exercise of control. New York: W. H. [ Links ]
Bausela, E. (2018). PISA 2012: Ansiedad y Bajo Rendimiento en Competencia Matemática. Revista Iberoamericana de Diagnóstico y Evaluación-e Avaliação Psicológica, 1(46), 161-173. doi: 10.21865/RIDEP46.1.12 [ Links ]
Bazán, J., Espinosa, G., & Farro, C. (2001). Rendimiento y actitudes hacia la Matemática en el sistema escolar peruano. Documento de Trabajo Nº 3, Programa MECEP (Medición de la Calidad Educativa Peruana). Lima: Ministerio de Educación. [ Links ]
Boaler, J. (1997). Setting, social class and survival of the quickest. British educational research journal, 23(5), 575-595. doi: 10.1080/0141192970230503 [ Links ]
Cardoso, E., Vanegas, E., & Cerecedo, M. (2012). Diagnóstico sobre las actitudes hacia las matemáticas del estudiantado que inicia sus estudios en tres posgrados en administración de empresas. Revista Electronica EDUCARE, 16(2), 237-253. doi: 10.15359/ree.16-2.15 [ Links ]
Chang, Y. (2015). Examining Relationships among Elementary Mathematics Teachers’ Efficacy and Their Students’ Mathematics Self-efficacy and Achievement. Eurasia Journal of Mathematics, Science and Technology Education, 11(6), 1307-1320. doi: 10.12973/eurasia.2015.1387a [ Links ]
Charalambous, C., Philippou, G., & Kyriakides, L. (2008). Tracing the development of preservice teachers’ efficacy beliefs in teaching mathematics during fieldwork. Educational Studies in Mathematics, 67(2), 125-142. [ Links ]
Colomeischi, A., & Colomeischi, T. (2015). The students ‘emotional life and their attitude toward mathematics learning. Procedia-Social and Behavioral Sciences, 180, 744-750. doi: 10.1016/j.sbspro.2015.02.192 [ Links ]
Cronbach, L. (1951). Coefficient alpha and the internal structure of tests. Psychometrika, 16, 1-16. [ Links ]
Cueto, S., Andrade, F. & León, J. (2003). Las actitudes de los estudiantes peruanos hacia la lectura, la escritura, la matemática y las lenguas indígenas. Documento de Trabajo Nº 44. Lima: GRADE. [ Links ]
Enochs, L., & Riggs, I. (1990). Further development of an elementary science teaching efficacy belief instrument: A preservice elementary scale. School Science and Mathematics, 90, 695-706. doi: 10.1111/j.1949-8594.1990.tb12048.x [ Links ]
Enochs, L., Smith, P., & Huinker, D. (2000). Establishing factorial validity of the mathematics teaching efficacy beliefs instrument. School Science and Mathematics, 100(4), 194-202. doi: 10.1111/j.1949-8594.2000.tb17256.x [ Links ]
Fennema, E., & Sherman, J. (1976). Fennema-Sherman mathematics attitudes scales: Instruments designed to measure attitudes toward the learning of mathematics by females and males. Journal for research in Mathematics Education, 7(5), 324-326. [ Links ]
Figueroa, S., Perez, A., Baccelli, S., Prieto, G., Moler, E., & Argentina, P. (2012). Actitudes hacia la estadística en estudiantes de ingeniería. Premisa, 52, 37-49. [ Links ]
Flores, W., & Auzmendi, E. (2018). Actitudes hacia las matemáticas en la enseñanza universitaria y su relación con las variables género y etnia. Profesorado, Revista de Currículum y Formación del Profesorado, 22(3), 231-251. doi: 10.30827/profesorado.v22i3.8000 [ Links ]
García, J., Martínez, M., & Inglés, C. (2013). ¿Cómo se relaciona la ansiedad escolar con el rendimiento académico? Revista Iberoamericana de Psicología y Salud, 4(1), 63-76. [ Links ]
George, D., & Mallery, P. (2003). SPSS for Windows step by step: A simple guide and reference. 11.0 update (4° ed.). Boston: Allyn & Bacon. [ Links ]
Goddard, R., Hoy, W., & Woolfolk, A. (2004). Collective efficacy beliefs: Theory developments, empirical evidence, and future directions. Educational researcher, 33(3), 3-13. doi: 10.3102/0013189X033003003 [ Links ]
Hassan, A. & Hassan, T. (2012). Science teaching self-efficacy and outcome expectancy beliefs of secondary school teachers in UAE. International Journal for Research in Education, 32, 1-22. [ Links ]
Hourigan, M., & Leavy, A. M. (2019). The influence of entry route to teaching on Irish pre-service primary teachers’ attitudes towards mathematics. Journal of Further and Higher Education, 43(7), 869-883. doi: 10.1080/0309877X.2017.1420148 [ Links ]
Incikabi, L. (2013). Teacher candidates’efficacy beliefs in mathematics: Play-generated curriculum instruction. Eurasia Journal of Mathematics, Science, & Technology Education, 9(2), 167-176. doi: 10.12973/eurasia.2013.927a [ Links ]
Kim, C., Park, S. W., & Cozart, J. (2014). Affective and motivational factors of learning in online mathematics courses. British Journal of Educational Technology, 45(1), 171-185. doi: 10.1111/j.1467-8535.2012.01382.x [ Links ]
Liu, C., Jack, B., & Chiu, H. (2007). Taiwan elementary teachers’ views of science teaching self-efficacy and outcome expectations. International Journal of Science and Mathematics Education, 6(1), 19-35. doi: 10.1007/s10763-006-9065-4 [ Links ]
Ma, X., & Kishor, N. (1997). Assessing the Relationship Between Attitude Toward Mathematics and Achievement in Mathematics: A Meta-Analysis. Journal for research in Mathematics Education, 28(1), 26-47. doi: 10.2307/749662 [ Links ]
Michaluk, L., Stoiko, R., Stewart, G., & Stewart, J. (2018). Beliefs and Attitudes about Science and Mathematics in Pre-Service Elementary Teachers, STEM, and Non STEM Majors in Undergraduate Physics Courses. Journal of Science Education and Technology, 27(2), 99-113. [ Links ]
Mohamed, L. & Waheed, H. (2011). Secondary students’ attitude towards mathematics in a selected school of Maldives. International Journal of humanities and social science, 1(15), 277-281. [ Links ]
Neale, D. (1969). The role of attitudes in learning mathematics. The Arithmetic Teacher, 16(8), 631-640. [ Links ]
Nicolaidou, M., & Philippou, G. (2003). Attitudes towards mathematics, self-efficacy and achievement in problem solving. En M. A. Mariotti (Ed.), European Research in Mathematics Education III (pp.1-11). Italy: University of Pisa. [ Links ]
Recber, S., Isiksal, M., & Koç, Y. (2018). Investigating self-efficacy, anxiety, attitudes and mathematics achievement regarding gender and school type. Annals of Psychology, 34(1), 41-51. doi: 10.6018/analesps.34.1.229571 [ Links ]
Salaya, A. (2006). La actitud hacia las matemáticas y el rendimiento académico. Revista Memorias, 7(1), 53-62. [ Links ]
Sancar, H. (2013). Effects of video-supported expertise-based training (XBT) on preservice science teachers’self-efficacy beliefs. Eurasia Journal of Mathematics, Science, & Technology Education, 9(2), 131-141. doi: 10.12973/eurasia.2013.924a [ Links ]
Schunk, D. H. (1991). Self-efficacy and academic motivation. Educational psychologist, 26(3-4), 207-231. doi: 10.1080/00461520.1991.9653133 [ Links ]
Segarra, J., & Julià, C. (2020). Mathematics Teaching Self-Efficacy and Outcome Expectancy of Pre-Service and In-Service Primary Education Teachers. Acta Scientiae, 22(6). doi: 10.17648/acta.scientiae.6049 [ Links ]
Shahid, F. & Ullah, S. (2008). Students' attitude towards mathematics. Pakistan Economic and Social Review, 46(1), 75-83. [ Links ]
Swars, S., Daane, C., & Giesen, J. (2006). Mathematics anxiety and mathematics teacher efficacy: What is the relationship in elementary preservice teachers? School Science and Mathematics, 106(7), 306-315. doi: 10.1111/j.1949-8594.2006.tb17921.x [ Links ]
Swars, S., Hart, L., Smith, S., Smith, M., & Tolar, T. (2007). A longitudinal study of elementary pre-service teachers' mathematics beliefs and content knowledge. School Science and Mathematics, 107(8), 325-335. doi: 10.1111/j.1949-8594.2007.tb17797.x [ Links ]
Takunyaci, M., & Takunyaci, M. (2014). Preschool teachers’ mathematics teaching efficacy belief. Procedia-Social and Behavioral Sciences, 152, 673-678. doi: 10.1016/j.sbspro.2014.09.261 [ Links ]
Tezer, M., & Karasel, N. (2010). Attitudes of primary school 2nd and 3rd grade students towards mathematics course. Procedia-Social and Behavioral Sciences, 2(2), 5808-5812. doi: 10.1016/j.sbspro.2010.03.947 [ Links ]
Ursini, S. & Sánchez, J. (2019). Actitudes hacia las matemáticas. Qué son. Cómo se miden. Cómo se evalúan. Cómo se modifican. Ciudad de México, México: UNAM, FES Zaragoza. [ Links ]
Ursini, S., & Sánchez, G. (2008). Gender, technology and attitude towards mathematics: a comparative longitudinal study with Mexican students. ZDM, 40(4), 559-577. [ Links ]
Zan, R., & Di Martino, P. (2007). Attitude toward mathematics: Overcoming the positive/negative dichotomy. The Montana Mathematics Enthusiast, 3(1), 157-168. [ Links ]
Correspondencia: Jaime Segarra. Universitat Rovira i Virgili, Spain. E-mail: jaimerodrigo.segarra@urv.cat
How to cite: Segarra, J. & Julià, C. (2021). Actitud hacia las matemáticas de los estudiantes de quinto grado de educación primaria y autoeficacia de los profesores. Ciencias Psicológicas, 15(1), e-2170. doi: https://doi.org/10.22235/cp.v15i1.2170
Authors' participation: a) Concepción y diseño del trabajo; b) Adquisición de datos; c) Análisis e interpretación de datos; d) Redacción del manuscrito; e) revisión crítica del manuscrito. J. S. has contributed in a, b, c, d, e; C. J. has contributed in a, c, d.
Received: May 18, 2020; Accepted: March 03, 2021










 texto en
texto en