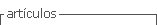EFECTOS GENERALES DE LAS VARIABLES ACTITUD Y ANSIEDAD

SOBRE EL RENDIMIENTO EN MATEMÁTICAS EN ALUMNOS DE

EDUCACIÓN SECUNDARIA OBLIGATORIA.

IMPLICACIONES PARA LA PRÁCTICA EDUCATIVA

 

 

ATTITUDE AND ANXIETY TOWARDS MATHEMATICS AND STUDENT ACHIEVEMENT IN SECONDARY EDUCATION. IMPLICATIONS FOR EDUCATIONAL PRACTICE

 

María Dorinda Mato Vázquez

Universidad de A Coruña, España

Jesús Miguel Muñoz Cantero

Universidad de A Coruña, España

 

Resumen: Los factores que influyen en el aprendizaje matemático son muy variados. Sin embargo, las actitudes son consideradas una de las variables que ejercen una influencia mayor en los resultados académicos de los estudiantes.

Este artículo presenta una investigación sobre los efectos de las variables actitud y ansiedad en el rendimiento matemático de alumnos de Educación Secundaria Obligatoria. Para ello se aplica un cuestionario de actitud y otro de ansiedad a una muestra de 1220 alumnos de Educación Secundaria Obligatoria. Se analizan las asociaciones e influencias de las variables (ansiedad y actitud) respecto al rendimiento mediante la correlación de Pearson y el procedimiento de regresión múltiple.

Son tres las conclusiones fundamentales: 1) La actitud tiene una correlación positiva con las calificaciones 2) Por el contrario, la ansiedad y el rendimiento tienen una correlación inversa y 3) Actitud y ansiedad correlacionan de forma negativa.

Palabras clave: Actitud, ansiedad, factores, rendimiento, matemáticas.

 

Abstract: Diverse factors affect the mathematical apprenticeship. However, attitudes are considered one of the most influential variables in student academic outcomes.

This paper presents an investigation on the effects of attitude and anxiety on mathematical achievement among secondary education students. Attitude and anxiety were assessed through two different scales in a sample of 1220 students. Data collected were analyzed using Pearson correlation and multiple regression analysis.

The authors came to three fundamental conclusions: 1) Attitude showed a positive correlation with grades 2) Anxiety and performance were inversely correlated and 3) Attitude and anxiety were negatively correlated.

Keywords: Attitude, anxiety, factors, performance, mathematics.

 

 

INTRODUCCIÓN

La matemática es considerada una asignatura fundamental en el currículum escolar, pese a ello, estudios recientes muestran que, en España, los rendimientos matemáticos son claramente insuficientes (U.M.C., 2005). Muchos alumnos encuentran las matemáticas difíciles y aburridas y les generan ansiedad e inseguridad.

 

Es conocido que altos niveles de ansiedad reducen la eficiencia en el aprendizaje, pues disminuyen la atención, concentración y retención, con el consecuente deterioro en el rendimiento escolar (Zubeidat, et al, 2007). Una forma usual de evitar esa ansiedad es prescindir de las asignaturas y carreras científicas (Ferrari & Scher, 2002; Onwuegbuzie, 2004; Scher & Osterman, 2002; Van Eerde, 2003).

 

¿Cuál es la razón para que esta asignatura sea una de las menos atrayentes para los estudiantes? ¿Cómo se puede motivar a los alumnos en las clases de matemáticas?

¿Qué papel puede jugar el profesor en el interés hacia la asignatura? ¿Existe relación entre las actitudes y calificaciones matemáticas? ¿Qué grado de ansiedad sufren los alumnos ante los exámenes de matemáticas?

 

Se aprende mejor aquello que produce agrado (Auzmendi, 1992). Igualmente, las experiencias previas ofrecen una fuerte influencia en el aprendizaje y las actitudes pueden provocar efectos negativos y ansiedad. Todo ello hace que la realización de las tareas matemáticas tienda a ser mala (Ashcraft, 2002). En cualquier caso, se sabe que los alumnos van tomando conciencia de sus capacidades, motivación o frustración hacia las matemáticas desde los primeros años y que, la ansiedad es mayor conformen avanzan los cursos (Opt’Eynde, DeCorte & Verschaffel, 2006; Broc Cavero, 2006).

 

La incidencia de las actitudes en el rendimiento de las matemáticas en los estudiantes de Educación Primaria (Ramírez, 2005), y en Educación Secundaria (Akey, 2006) ha confirmado que estas variables tienen una correlación positiva. Es más, muchos estudiantes no tienen problemas en otras materias y sin embargo se ponen nerviosos en las clases y sienten fuerte ansiedad ante los exámenes de matemáticas (Vigil-Colet, Lorenzo-Seva & Condon, 2008). Por tanto, es necesario promover la implicación de los profesores en el logro de habilidades matemáticas que favorezcan la mejora de las actitudes y la prevención de la ansiedad. Sin embargo, no todos los educadores están concienciados para valorarlas, pues, aunque se asume su importancia desde un punto de vista teórico, en la práctica, integrar los factores afectivos en los centros de enseñanza está por lograr (Gómez Chacón, 2000).

 

La preocupación por el estudio de los procesos de aprendizaje no es nueva. No obstante, esta cuestión adquiere un renovado interés en los últimos años, dando lugar a numerosos trabajos (Barca, Peralbo, & Brenilla, 2004; Bermejo, 2005; Carbonero & Navarro 2006).

 

Los datos aportados por este estudio permiten reflexionar sobre la importancia de las relaciones afectivas en el proceso de aprendizaje matemático.

 

FUNDAMENTACIÓN TEÓRICA

 

Desde hace décadas hay cierto consenso en admitir que los factores afectivos (actitudes, creencias y emociones) tienen una influencia destacable en el aprendizaje de las matemáticas (Zan, Brown, Evans & Hannula 2006). Más en concreto, las actitudes constituyen uno de los factores más importantes y más ampliamente estudiados (Guerrero, Blanco & Gil, 2006).

 

Vygostky (1991) planteó que uno de los principales defectos de la psicología tradicional fue la separación entre los aspectos intelectuales y los afectivos. Para Gargallo, et al. (2007) las actitudes son una predisposición aprendida, relativamente duradera, a evaluar de determinado modo a un objeto, persona, grupo, suceso o situación. Esta evaluación se hace a partir de las creencias disponibles en torno a los mismos, y produce actuaciones favorables o no sobre ese objeto, persona, grupo, suceso o situación, de manera consecuente con dicha evaluación.

 

Así, las actitudes expresan algún grado de aprobación o desaprobación para actuar sobre el objeto de la actitud (U.M.C., 2001). Por ejemplo, un estudiante ante las matemáticas (objeto de actitud) puede mostrar una actitud favorable cuando afirma que le gustan las clases, hace sus tareas, cree que es importante o muestra interés por leer libros de matemáticas.

 

Las actitudes tienen un carácter multidimensional que integra componentes cognitivo, afectivo-evaluativo y conductuales. Para la mayoría de los autores el componente afectivo-evaluativo es el elemento esencial de la actitud (Estrada, Batanero & Fortuny, 2003; Gil, Blanco & Guerrero, 2005). Es por esto que un profesor no debe centrarse únicamente en conseguir que los alumnos aprendan conocimientos (componente cognitivo), sino que mejorar las actitudes y descubrir el placer matemático es, al menos, tan importante. Asimismo, en la interacción que el profesor y el alumno establecen en la escuela, los factores afectivos de ambos ejercen influencia decisiva (Bazán, et al, 2006).

 

En esta línea de investigación basada en la relación entre actitudes y rendimiento académico, Aparicio y Bazán (2006), señalaron que un mayor incremento de conocimientos produce un cambio favorable en las actitudes.

Igualmente, cuando se planifica un cambio en las actitudes, lo que se hace es una serie de tareas (actividades) encaminadas hacia un cambio en la predisposición de pensar (cognitivo) respecto del objeto, mediante sentimientos más positivos (afectividad).

 

Otros estudios han revelado que el desarrollo de actitudes positivas es importante para el conocimiento de la asignatura, para la autoeficacia, y para evitar la ansiedad y la frustración (Relich & Way, 1994).

 

La relación entre las actitudes, la ansiedad y el rendimiento académico en Matemáticas ha sido revisada en diversas investigaciones, comprobando que las actitudes negativas correlacionan con un bajo rendimiento (Aliaga & Pecho, 2000) y con niveles altos de ansiedad (Magalhães, 2007).

 

También los procesos de socialización escolar son factores determinantes de ansiedad. La experiencia de fracasos reiterados, las interacciones punitivas con los adultos, la crítica mordaz en el aula o la ausencia de apoyo de los profesores, contribuyen a la instauración de una percepción amenazadora de las tareas escolares. En estas circunstancias la motivación de los alumnos se dirige únicamente a evitar el fracaso en la asignatura, en detrimento del interés por aprender (Rosario, Costa, Mourao, González-Pienda y Núñez, 2007). La motivación de los estudiantes es importante porque favorece patrones cognitivos cualitativamente diferentes y contribuye al desarrollo de la autorregulación (Suárez Riveiro, Anaya Nieto y Fernández Suárez, 2005).

 

Un estudiante ansioso está excesivamente preocupado por su progreso en clase, por no entender lo que su profesor está explicando o lo que éste espera de él (Kazelskis, 2000); teme salir a la pizarra, se angustia antes y durante los exámenes (Cassady, 2002) y, se inquieta cuando tiene que realizar operaciones aritméticas con un límite de tiempo o ante tareas complejas (Dutke & Stöber, 2001).

 

Para Onwuegbuzie (2003) la ansiedad hacia las matemáticas no es sólo un factor que causa una mala realización matemática en una persona ansiosa. Tampoco es el factor que interviene cuando hay una mala actitud hacia la asignatura. En muchas ocasiones, se convierte en un fenómeno intenso que provoca emociones poderosas de evitación en cursos posteriores (Hancock, 2001).

 

Sin embargo, González Ordi y Tobal (2001), se preguntan si el alumno ansioso tiene un mal rendimiento porque está demasiado preocupado o, por el contrario, está preocupado porque no consigue un buen rendimiento y no sabe cómo mejorarlo. Probablemente ninguna de las dos hipótesis es válida para todos los casos. La ansiedad en función de la situación puede ser el desencadenante de un mal rendimiento, ser consecuencia de él o ejercer ambos roles al mismo tiempo.

 

También se debe considerar el hecho de que el profesor pueda presentar manifestaciones negativas o positivas de acuerdo con sus experiencias en el pasado. Las dificultades, tanto en el aprendizaje como en la enseñanza, pueden estar relacionadas con esas actitudes. A este respecto, las investigaciones de Hofflich, Hughes y Kendall (2006) sugieren que existe una relación entre actitudes, creencias del profesor y rendimiento, y entre las actitudes, las creencias y el rendimiento de sus alumnos. Así, por ejemplo, si un alumno llega a clase con una mala predisposición ante la Matemática, la solución de factores externos no ayudará en mucho a su rendimiento si antes no se intenta mejorar su disposición hacia el aprendizaje y sus actitudes frente a la asignatura.

 

Pero también hay investigaciones que no han encontrado asociación entre las actitudes, la ansiedad y el rendimiento en Matemáticas (Cueto, Andrade & León, 2003). Sin embargo, aunque algunos resultados discrepan, la mayoría de los investigadores hallaron correlaciones significativas (Tárraga, 2008).

 

OBJETIVOS

 

Los objetivos prioritarios de este estudio son dos:

Analizar la incidencia de las variables actitud y ansiedad en el rendimiento académico en matemáticas de los alumnos de ESO.

Analizar cómo ambas variables se ven influenciadas entre sí.

 

MÉTODO

Muestra

La muestra está constituida por un total de 1220 alumnos (586 chicos y 634 chicas) de 1º a 4º curso de Educación Secundaria Obligatoria pertenecientes a diferentes colegios públicos y concertados, elegidos al azar, de la ciudad de A Coruña. La edad media de los alumnos de la muestra es de 13´5 años.

 

El hecho de centrarnos en este grupo de edad viene determinada por considerar que es en la ESO cuando los alumnos muestran una clara actitud (positiva o negativa) hacia las matemáticas y manifiestan más ansiedad ante ellas. No en vano los estudios al respecto, reconocen que el 68% de los estudiantes de los 12 a los 16 años que van a clase de matemáticas experimentan altos niveles de ansiedad (Norwood, 1994). Éste es un porcentaje alto si consideramos que esta asignatura es obligatoria para todos los alumnos hasta terminar la Educación Secundaria.

 

La distribución muestral queda reflejada en la Tabla 1.

 

 

 Procedimiento

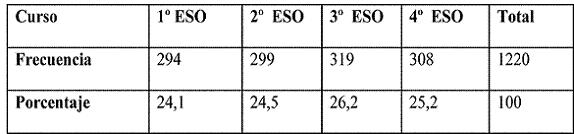
Se utilizan dos cuestionarios, uno para evaluar las actitudes y otro para la ansiedad elaborados por Mato (2006). Ambos adoptan el formato de las escalas tipo Likert, con cinco opciones de respuesta, que van desde “muy en desacuerdo” hasta “muy de acuerdo”. La aplicación se realizó con la ayuda de los profesores de los distintos grupos.

 

El “Cuestionario de Actitud” tiene una fiabilidad α de Cronbach de .9706 y consta de 19 ítems repartidos en dos factores: “actitud del profesor percibida por los alumnos” “agrado y utilidad de las matemáticas en el futuro”.

 

El primer factor comprende 11 ítems y describe la percepción que tienen los estudiantes sobre las actitudes de su profesor de matemáticas. Hace referencia al trato que tiene el profesor con sus alumnos, cómo los anima, si las clases son participativas, etc.

 

El segundo factor comprende 8 ítems y describe la satisfacción que siente el estudiante hacia el estudio de las matemáticas y la confianza que tiene en sí mismo. Informa además del valor que el estudiante da a las matemáticas de cara al futuro.

 

El “Cuestionario de ansiedad” tiene una fiabilidad de 0,9504 y consta de 24 ítems repartidos en 5 factores: “ansiedad ante la evaluación de matemáticas”, “ansiedad ante la temporalidad”, “ansiedad ante la comprensión de problemas”, “ansiedad frente a los números y operaciones matemáticas” y “ansiedad ante situaciones matemáticas de la vida real”.

 

El primer factor comprende 11 ítems y se refiere al sentimiento de ansiedad y temor que el alumno manifiesta al ser evaluado.

 

El segundo factor comprende 4 ítems y explica la ansiedad que sienten los alumnos ante el tiempo que le queda para hacer un examen o para llevar los ejercicios hechos para clase.

 

El tercer factor comprende 3 ítems y se refiere a si el alumno siente temor ante la comprensión de los problemas de matemáticas.

 

El cuarto factor comprende 3 ítems y describe la ansiedad que el alumno manifiesta al hacer ejercicios, operaciones y, en general, al trabajar con números.

 

Por último, el quinto factor comprende 3 ítems y describe a la ansiedad que siente el alumno al tener que enfrentarse a las matemáticas en la vida real.

 

La aplicación se realizó a 1220 alumnos de ESO (586 chicos y 634 chicas), pertenecientes a siete centros (dos aulas de cada nivel escolar) resultando un total de 56 grupos. Los centros cubren las características propias de la población: dos colegios públicos del centro y dos de la periferia de la ciudad, un centro de enseñanza privada y dos centros de enseñanza concertada. La razón de optar por uno o dos centros de enseñanza privada, pública o concertada es para respetar la proporción de centros y de alumnos de cada tipo que hay en la ciudad, para que la investigación resulte lo más representativa posible.

 

La puesta en contacto con los colegios se hace en un primer momento telefónicamente con cada uno de los directores de los centros. Posteriormente hay una entrevista en la que participan el director del departamento de orientación, el orientador y el investigador, en la cual se le explican los motivos de la investigación y de qué consta la misma. Se pide que sea el orientador del centro el que aplique los cuestionarios, de forma colectiva, solicitando que no estuviera presente en el aula el profesor de matemáticas durante la aplicación de las pruebas con el fin de no mediatizar las respuestas de los alumnos (algunas ítems se refieren a las relaciones entre el profesor y el alumno). Por lo tanto, los cuestionarios se aplican en cada centro por personal diferente, pero que previamente es preparado y entrenado, a fin de evitar que personas desconocidas para los alumnos les causaran alguna intranquilidad.

 

Para cumplimentar los cuestionarios se ofrecieron a los alumnos las siguientes instrucciones:

·      Lo que vamos a realizar a continuación nada tiene que ver con la escuela, es decir, los resultados de lo que hagáis no lo verán vuestros profesores y podéis estar tranquilos porque no forma parte de la evaluación académica. Además los datos sólo los verá el investigador.

·         Es importante que seáis sinceros en vuestras contestaciones, que tengáis una actitud positiva y que estéis concentrados en lo que hacéis.

·         Si hay algún alumno que no desee realizar las pruebas puede optar libremente por ello.

·     También es importante que no dejéis ninguna pregunta en blanco, hay que contestar todas las cuestiones. Si alguno/a no está seguro, debe pensar un poco y responder lo que más se acerque a lo que piensa. Si después de comenzar surgen algunas dudas permaneced en vuestra silla y levantad el brazo, nosotros iremos hasta allí y resolveremos en voz baja la duda, es decir si no sabéis contestarla nos aclaráis el motivo. ¡Podéis comenzar!.

 

No se impuso limitación de tiempo; sin embargo, los alumnos tardaron en completar los cuestionarios entre 30 y 45 minutos en todos los grupos. Para evitar que aquellos estudiantes que no estaban interesados en dichos cuestionarios influyeran negativamente en los que sí lo estaban, convenimos que nadie saliera del aula hasta que todos hubiesen acabado. Los que iban finalizando podían dedicarse a cualquier otra tarea de su interés, lo que favoreció que los cuestionarios no fueran contestados apresuradamente, influidos por los que habían concluido antes.

 

Elegimos también el horario lectivo para evitar esa desgana manifiesta que generalmente se tiene a contestar encuestas, de esta forma intercambiábamos contenidos de otras asignaturas por cuestionarios.

 

Los cuestionarios se recogieron una vez que observamos que todos los alumnos habían finalizado.

 

Resultados

 

Se utilizó un análisis de varianza (ANOVA) parSe utilizó un análisis de varianza (ANOVA) para contrastar la existencia de diferencias significativas entre las variables actitud y ansiedad respecto al rendimiento de los alumnos en matemáticas al finalizar el curso anterior (suspenso, aprobado, bien, notable, sobresaliente). La calificación correspondiente es la obtenida por los sujetos mediante pruebas orales, escritas, trabajos en grupo, cuadernos, actitud en clase…

 

Para conocer los efectos generales y específicos de las variables sobre el rendimiento se utilizó la correlación de Pearson y la regresión múltiple.

 

Para ello se planteó la ecuación que maximiza la predicción de la variable rendimiento determinando el mayor agregado ponderado de las variables predictoras, actitud y ansiedad (Gardner, 2001). El método utilizado es el de pasos sucesivos.

 

Análisis de la relación entre actitud, ansiedad y rendimiento en matemáticas.

Los resultados del análisis de varianza indican que las diferencias en las puntuaciones obtenidas en valores de ansiedad total y de actitud, a nivel general, son significativas con valores de ,003 y ,000 respectivamente (Tabla 2). En el caso de la variable ansiedad, estas diferencias no aparecen tomando por separado los factores “ansiedad ante la temporalidad”, “ansiedad ante la comprensión de problemas” y “ansiedad ante situaciones de la vida real” en función de las calificaciones de los estudiantes. Sin embargo, estas diferencias sí se dan en los factores “ansiedad ante la evaluación” y “ansiedad frente a los números y las operaciones matemáticas”.

 

Tabla 2. ANOVA. Actitud-ansiedad-rendimiento

 

 

En el caso de la variable actitud hay diferencias significativas respecto a la calificación de los estudiantes en cuanto a los factores “actitud del profesor percibida por el alumno” y “agrado y utilidad de las matemáticas”.

 

De las comparaciones entre los grupos, a fin de detectar a cuál de ellos se deben las diferencias, se observaron diferencias de ansiedad entre aquellos sujetos con un rendimiento de suspenso y notable respecto a la “ansiedad total”; más concretamente, ante el factor “ansiedad ante la evaluación”. No existían diferencias entre las otras categorías del rendimiento.

 

De igual modo, respecto a la variable actitud, se observaron diferencias significativas en todas las categorías de rendimiento respecto a la actitud general.

 

Por el contrario, no existen diferencias de rendimiento respecto al factor “actitud del profesor percibida por el alumno” cuando se cruzan las calificaciones superiores (bien, notable y sobresaliente). Sí se observó que existían diferencias significativas en cuanto al factor “agrado y utilidad de las matemáticas” respecto a todas las categorías del rendimiento.

 

En la variable ansiedad, dado que las diferencias no son significativas, todas las categorías de la variable “rendimiento” forman un grupo.

 

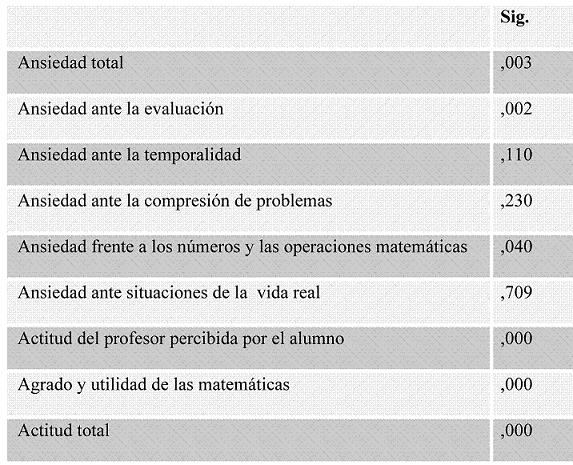
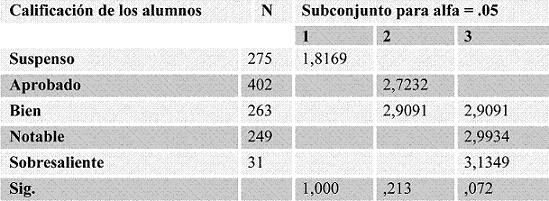
Algo similar ocurre referente a la variable actitud, en el factor “actitud del profesor percibida por el alumno”, en el que la categoría “suspenso” forma un grupo, las categorías “aprobado” y “bien” forman otro y, las categorías “bien”, “notable” y “sobresaliente”, un tercero (Tabla 3). En el caso del factor “agrado y utilidad de las matemáticas” cada una de las categorías forma un grupo (Tabla 4).

 

Tabla 3. Actitud del profesor percibida por el alumno-rendimiento

 

 

Tabla 4. Agrado y utilidad de las matemáticas-rendimiento

 

 

Efectos generales de la variables actitud y ansiedad sobre el rendimiento.

 

Para analizar las asociaciones e influencias entre las variables utilizadas se utilizó la correlación de Pearson entre las tres variables y los factores en que se descomponen.

 

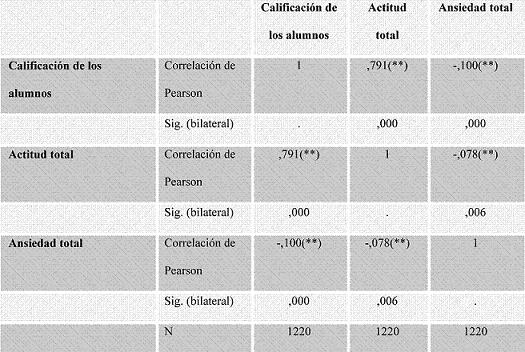
Los resultados que se exponen en la Tabla 5 muestran la existencia de correlaciones significativas entre ellas. Se observó que la actitud y la calificación de los alumnos tiene una correlación positiva y relativamente alta y significativa (,791); es decir que a medida que la actitud es más positiva los sujetos obtienen mayores calificaciones.

 

Tabla 5. Correlaciones actitud-ansiedad-rendimiento

 

** La correlación es significativa al nivel 0,01 (bilateral).

No ocurre lo mismo con la ansiedad y el rendimiento, donde se produce una relación inversa, es decir, a medida que la ansiedad aumenta el rendimiento disminuye.

 

La actitud correlaciona así mismo de manera negativa con la ansiedad, lo que implica que a medida que la actitud es menor (-,078) la ansiedad es mayor (en términos generales) siendo significativas a ,005 y ,001.

 

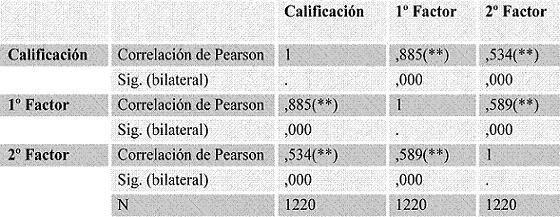
Posteriormente se ha analizado la correlación de las calificaciones obtenidas por los sujetos en matemáticas con los factores de actitud. Los resultados muestran valores positivos y significativos en todos los casos, de forma que las calificaciones aumentan cuando es mayor el “agrado y la utilidad de las matemáticas” y la “actitud del profesor percibida por el alumno”.

 

Estos valores se consideran altos, pues se obtienen correlaciones de ,885 entre la calificación y la utilidad de las matemáticas y de ,534 entre la calificación y “la actitud del profesor percibida por el alumno” (Tabla 6).

 

Tabla 6. Correlaciones calificaciones-factores de actitud

 

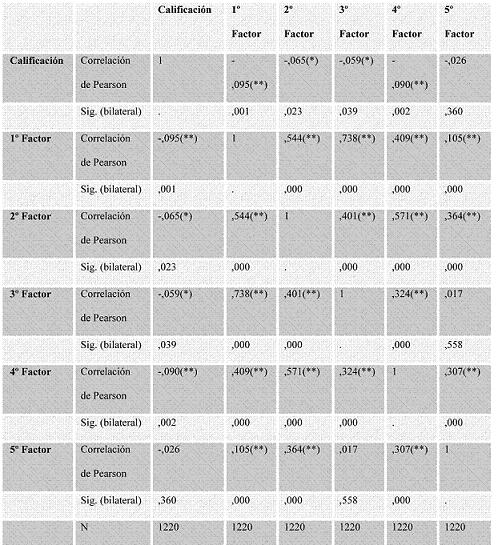
Así mismo, existe una correlación negativa (significativa al 0.01), entre cada uno de los factores de la ansiedad y la calificación obtenida en matemáticas, para la “ansiedad ante la evaluación” y “ansiedad frente a los números y las operaciones matemáticas” y al 0,05 en los factores referidos a “ansiedad ante la temporalidad” y “ansiedad ante la comprensión de problemas”. El único valor cuya correlación no es significativa es ante el factor “ansiedad ante situaciones de la vida real (-,026).

 

El signo (negativo) de los valores indica que a mayor ansiedad el rendimiento disminuye.

 

En lo que concierne a la relación existente entre los diferentes factores de la ansiedad existe una correlación significativa entre todos con la única excepción entre los factores “ansiedad ante la comprensión de problemas” y “ansiedad ante situaciones de la vida real” con un valor de ,017 (Tabla 7).

 

Tabla 7. Correlaciones calificaciones-factores de ansiedad

 

** La correlación es significativa al nivel 0,01 (bilateral).

* La correlación es significante al nivel 0,05 (bilateral).

Posteriormente, se realizó un análisis de regresión múltiple con el fin de detectar la proporción de la variable “rendimiento en matemáticas” (medida por la calificación que obtuvieron los sujetos) que es explicada por los factores referidos a la actitud. La ecuación de regresión obtenida y sus coeficientes ayudaron a determinar el poder predictivo de las variables independientes (actitud y ansiedad) sobre la dependiente (calificación obtenida en matemáticas).

 

Aunque los factores de ansiedad muestran correlaciones muy bajas se incorporan al análisis de correlación múltiple. La interpretación se realizó a través del coeficiente de determinación (R2). Para ello se introdujo en el programa estadístico SPSS como variable dependiente el rendimiento de los sujetos y como variables independientes la actitud y ansiedad.

 

La Tabla 8 muestra los dos modelos generados por el sistema donde las variables introducidas han sido los dos factores referidos a la actitud. La probabilidad asociada a F es la que por defecto da el sistema (0,05).

 

Tabla 8. Variables introducidas/eliminadas (b)

 

A: Todas las variables solicitadas introducidas.

B: Variable dependiente: Calificación que obtuviste en matemáticas en el curso pasado.

 

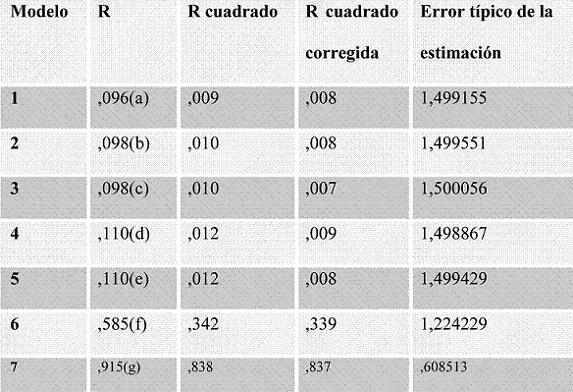
En la Tabla 9, figuran los coeficientes de correlación múltiple y los coeficientes de determinación (corregido y no corregido) para cada uno de los dos modelos.

 

No obstante, no existen grandes diferencias entre ambos parámetros.

 

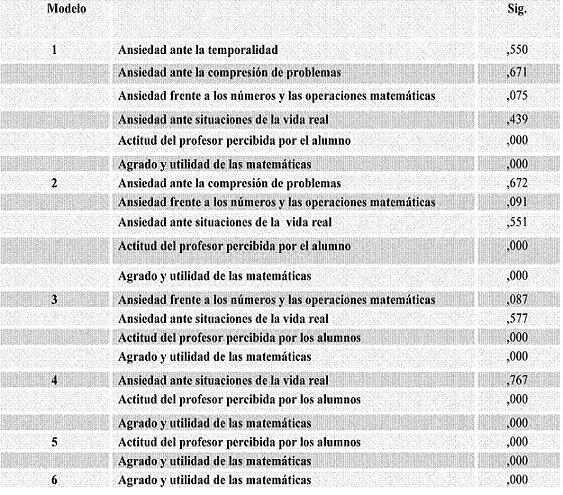
El valor de R cuadrado muestra que la proporción de la variable dependiente explicada por el modelo es bastante baja hasta la incorporación de las variables referidas a la actitud (actitud del profesor percibida por el alumno y agrado y utilidad de las matemáticas) aumentando de ,012 a ,342 cuando se incorpora “actitud del profesor percibida por el alumno” y ,838 cuando el factor a incorporar es el referido a “agrado y utilidad de las matemáticas”. La diferencia entre el quinto modelo (que incorpora solo aquellas variables referidas a la ansiedad) y el sexto modelo es de ,330 y de éste sobre el séptimo de ,496. (Tabla 9).

 

Tabla 9. Resumen del modelo

A: Variables predictoras: (Constante), ansiedad ante la evaluación.

B: Variables predictoras: (Constante), ansiedad ante la evaluación, ansiedad ante la temporalidad.

C: Variables predictoras: (Constante), ansiedad ante la evaluación, ansiedad ante la temporalidad, ansiedad ante la compresión de problemas.

D: Variables predictoras: (Constante), ansiedad ante la evaluación, ansiedad ante la temporalidad, ansiedad ante la compresión de problemas, ansiedad frente a los números y las operaciones matemáticas.

E: Variables predictoras: (Constante), ansiedad ante la evaluación, ansiedad ante la temporalidad, ansiedad ante la compresión de problemas, ansiedad frente a los números y las operaciones matemáticas, ansiedad ante situaciones de la vida real.

F: Variables predictoras: (Constante), ansiedad ante la evaluación, ansiedad ante la temporalidad, ansiedad ante la compresión de problemas, ansiedad frente a los números y las operaciones matemáticas, ansiedad ante situaciones de la vida real, actitud del profesor percibida por el alumno.

G: Variables predictoras: (Constante), ansiedad ante la evaluación, ansiedad ante la temporalidad, ansiedad ante la compresión de problemas, ansiedad frente a los números y las operaciones matemáticas, ansiedad ante situaciones de la vida real, actitud del profesor percibida por el alumno, agrado y utilidad de las matemáticas.

 

Las entradas de los coeficientes se han realizado paso a paso con sus correspondientes ecuaciones de regresión simple o múltiple.

Destaca que el único valor significativo de los referidos a la variable ansiedad es el de “ansiedad ante la evaluación”, siendo de ,001 en el primer modelo y de ,012 en el segundo, donde su unión con la “ansiedad ante la temporalidad” coproduce esas diferencias.

 

Otros valores significativos son los referidos a la incorporación de los factores referidos a la variable actitud (“actitud del profesor percibida

por los alumnos” y “agrado y utilidad de las matemáticas”) obteniéndose valores significativos en los modelos 6 y 7 establecidos (valor de significación de ,000 en ambos casos).

 

También aparecieron valores negativos en los coeficientes Beta para los factores referidos a la ansiedad. Esto indica una influencia negativa sobre el rendimiento en las matemáticas, actuando como factor predictor negativo (solamente el factor referido a “ansiedad ante la comprensión de problemas” presenta valores positivos, aunque muy bajos para comportarse como factor predictor ,032). (Tabla 10).

 

A: Variable dependiente: Calificación que obtuviste en matemáticas en el curso pasado.

Por último se halló el coeficiente de regresión estandarizado. Los valores más altos se encontraron en las variables referidas a los factores de actitud.

 

El factor referido a “agrado y utilidad de las matemáticas” es el que mejor predice la variable dependiente. Los valores altos de colinealidad entre las variables mostraron que la combinación de las variables independientes, especialmente de los valores referidos a la actitud, influyen mucho para explicar la variable dependiente.

 

Solamente el valor referido a “ansiedad ante la comprensión de problemas” presentó valores más bajos que el resto (,456). (Tabla 11).

 

Tabla 11. Variables excluidas (g)

 

A: Variables predictoras en el modelo: (Constante), ansiedad ante la evaluación.

B: Variables predictoras en el modelo: (Constante), ansiedad ante la evaluación, ansiedad ante la temporalidad.

C: Variables predictoras en el modelo: (Constante), ansiedad ante la evaluación, ansiedad ante la temporalidad, ansiedad ante la compresión de problemas.

D: Variables predictoras en el modelo: (Constante), ansiedad ante la evaluación, ansiedad ante la temporalidad, ansiedad ante la compresión de problemas, ansiedad frente a los números y las operaciones matemáticas.

E: Variables predictoras en el modelo: (Constante), ansiedad ante la evaluación, ansiedad ante la temporalidad, alos números y las operaciones matemáticas, ansiedad ante situaciones de la vida real.

F: Variables predictoras en el modelo: (Constante), ansiedad ante la evaluación, ansiedad ante la temporalidad, ansiedad ante la compresión de problemas, ansiedad frente a los números y las operaciones matemáticas, ansiedad ante situaciones de la vida real, actitud del profesor percibida por el alumno.

G: Variable dependiente: Calificación que obtuviste en matemáticas en el curso pasado.

 

Estas coincidencias nos estimulan a proponer la implementación de metodologías de enseñanza que eviten la desmotivación por el aprendizaje, el fracaso en la resolución de problemas, las reacciones negativas ante los problemas que se le presentan en la vida cotidiana y el pánico a la hora de ser evaluados en matemáticas.

 

Las aportaciones también permiten reflexionar sobre la necesidad de mejorar la interacción entre el profesor y el alumno con el fin de desarrollar buenas actitudes hacia el aprendizaje matemático (Ramírez, 2005, Akey, 2006, Bazán, et al., 2006; Broc Cavero, 2006; Fierro-Hernández, 2006; Gargallo, et al, 2007).

 

Sin embargo, queremos llamar la atención sobre la falta de estudios acerca de la correlación entre cada uno de los factores de actitud y el rendimiento, los factores de ansiedad y rendimiento y la correlación actitud-ansiedad-rendimiento.

 

Es cierto que no es sólo cuestión de actitudes y de ansiedad, sería necesario profundizar en las características que acompañan a los grupos de estudiantes para completar su perfil, nivel de estrategias que utilizan, enfoques de aprendizaje, autoconcepto, variables sociofamiliares, etc. Ello desborda los límites de este trabajo y es tarea a abordar en futuras investigaciones que permitan hacer los patrones de intervención más completos. Sin embargo se tiene claro que la reducción de la ansiedad y la mejora de las actitudes hacia las matemáticas, se constituye como un objetivo relevante pues los aspectos afectivos positivos no sólo ayudan a explicar el rendimiento de los alumnos, sino que también son por sí mismos un resultado importante de la educación.

 

REFERENCIAS

Aliaga, J. y Pecho J. (2000). Evaluación de la actitud hacia la Matemática en estudiantes secundarios. Revista Paradigmas, 1(1-2), 61-78.

Aparicio, A. y Bazán, J. L. (2006). Actitudes hacia la estadística en profesores de nivel primario. En González, M., Bazán, J., Sánchez, R. (Editores). Coloquios de Matemática Educativa. Reportes de Investigación. Serie C, 18, Parte 2, 125-131. PUCP.

Akey, T. (2006). School context, student attitudes and behaviour, and academic achievement: An exploratory analysis. Informe de investigación. Recuperado en 2006, en http://www.eric.ed.gov/ERICDocs/data/ericdocs2/content_storage_

Ashcraft, M. H. (2002). Math Anxiety: Personal, Educational, and Cognitive Consequences. Current Directions in Psychological Sciences, 11, 5, 181-185. AUZMENDI, E. (1992). Las actitudes hacia la matemática-estadística en las enseñanzas medias y universitaria. Características y medición. Bilbao. Mensajero.

Barca, A., Peralbo, M. y Brenilla, J. C. (2004). Atribuciones causales y enfoques de aprendizaje. La escala Siacepa. Psicothema, 16 (1), 94 – 103.

Bazán, J. L. y Aparicio A. S. (2006). Las actitudes hacia la Matemática-Estadística dentro de un modelo de aprendizaje. Revista Semestral del Departamento de Educación, XV, 28, 1-12.

Bermejo, V. (2005). Microgénesis y cambio cognitivo: adquisición del cardinal numérico. Psicothema, 17(4), 559-562.

Broc Cavero, M. A. (2006) Motivación y rendimiento académico en alumnos de Educación Secundaria Obligatoria y Bachillerato LOGSE. Revista de Educación 340, 379-414.

Carbonero, M. A. y Navarro, J.C. (2006). Entrenamiento de alumnos de Educación superior en estrategias de aprendizaje en Matemáticas. Psicothema,18(3), 348-352.

Cassady, J. (2002). Cognitive Test Anxiety and Academic Performance. Contemporary Educational Psychology, 27(2), 270-295.

Cueto, S., Andrade, F. y León, J. (2003). Las actitudes de los estudiantes peruanos hacia la lectura, la escritura, la matemática y las lenguas indígenas. Lima. GRADE, 2003. 75 P. (Documento de Trabajo, 44).

Dutke, S. y Stöber, J. (2001). Test anxiety, working memory and cognitive performance: Supportive effects of sequential demands. Cognition & Emotion, 15(3), 381-389.

Estrada, A., Batanero, C. y Fortuny, J. M. (2003). Actitudes y Estadistica en profesores en formación y en ejercicio. En: Edicions de la Universitat de Lleida Actas del 27 Congreso Nacional de Estadística e Investigación Operativa. Universidad de Lleida. CD ROM.

Ferrari, J., y Scher, S. (2002). Toward an understanding of academic and non academic tasks procrastinated by students: The use of daily logs. Psychology in the Schools, 37(4), 359-366.

Fierro-Hernández, C. (2006). Valoración del impacto de un programa de educación en valores en el último curso de Educación Secundaria obligatoria. Revista de Educación, 339, 455-466.

Gardner, R. C. (2001). Psychological Statistics Using SPSS for Windows. Upper Saddle River, NJ: Prentice Hall. [Trad. Esp. (2003): Estadística para Pssicología usando SPSS para Windows. Naucalpan de Juárez, Edo. De México: Pearson Education/ Prentice Hall].

Gargallo, B., Pérez, C., Sánchez, F., Serra, B., Ros,I. (2007). Actitudes ante el aprendizaje y rendimiento académico en los estudiantes universitarios. Revista Iberoamericana de Educación, 42/1. OEI.

Gil, N., Blanco, L. y Guerrero, E. (2005). El dominio afectivo en el aprendizaje de las matemáticas. Una revisión de de sus descriptores básicos. Unión Revista Iberoamericana de Educación Matemática. 2, 15-32.

Gómez Chacón, I. M. (2000). Matemática emocional. Los afectos en el aprendizaje matemático. Madrid. Narcea. González Ordi, H. y Tobal, J. J. (2001). La sugestionabilidad como variable moduladora en la imaginación de escenas ansiógenas. Ansiedad y Estrés, 7 (1), 89-110.

Guerrero, E. Blanco, L. y Gil, N. (2006). El papel de la afectividad en la resolución de problemas matemáticos. Revista de Educación, 340, 551-569

Hancock, D. (2001). Effects of Test Anxiety and Evaluative Threat on Students’ Achievement and Motivation. Journal of Educational Research, 94 (5), 284-90.

Hofflich, A., Hughes, A., y Kendall, P. (2006). Somatic complaints and childhood anxiety disorders. International Journal of Clinical and Health Psychology, 6, 229-242. KAZELSKIS, R. (2000). Mathematics Anxiety and Test Anxiety: Separate constructs? Journal of Experimental Education, v. 68 (2), 137-146.

Magalhaes, A. (2007). Ansiedade face aos Testes, Género e Rendimento Académico: um estudo no Ensino Básico. Tese de mestrado, Faculdade de Psicologia e Ciências da Educação, Universidade do Minho.

Mato, M. D. (2006). Diseño y validación de dos cuestionarios para evaluar las actitudes y la ansiedad hacia las matemáticas en alumnos de Educación Secundaria Obligatoria. Tesis inédita. Universidad de La Coruña.

Norwood, K. S. (1994). The Effect of Instructional Approach on Mathematics Anxiety and Achievement. School Science and Mathematics, 94, 248-254.

Onwuegbuzie, A. J. (2003). Modeling statistics achievement among graduate students. Educational and Psychological measurement, 63 (6), 1020-1038.

Onwuegbuzie, A. J. (2004). Academic procrastination and statistics anxiety. Assessment & Evaluation in Higher Education, 29(1), 3-19.

Opt’eynde, Decorte, E. y Verschaffel, L. (2006). Accepting emotional complexity:a socio-constructivist perspective on the role of emotions in the mathematics classroom. Educational Studies in Mathematics, 63, 193-207.

Ramírez, M. J. (2005). Actitudes hacia las matemáticas y rendimiento académico entre estudiantes de octavo básico. Estudios pedagógicos, 31 (1), 97-112.

Relich, J.. y Way, J. (1994). Measuring pre-Service Teachers Attitudes to Mathematics: Further Developments of a Questionnaire. In Da Ponte, J. P. y Matos, J. F. Proceedings of the Eighteenth International Conference for the psychology of Mathematics Education, 4, 105-112. Lisbon. Portugal.

Rosario, P., Costa, M., Mourao, R., Núñez, J.C., González-Pienda, J.A., y Valle, A. (2007). Procastination, SRL and Math achievement. Academic Exchange Quarterly, 11(4), 23-28.

Schier, S., y Osterman, N. (2002). Procrastination, conscientiousness, anxiety, and goals: Exploring the measurement and correlates of procrastination among school-aged children. Psychology in the Schools, 39(4), 385-398.

Suárez Riveiro, J. M., Anaya Nieto, D. y Fernández Suárez, A. P. (2005). Sobre la determinación motivacional del aprendizaje autorregulado. Revista de Educación, 338, 295-308.

Tárraga, R. (2008). Relación entre rendimiento en solución de problemas y factores afectivo-motivacionales en alumnos con y sin dificultades del aprendizaje. Apuntes de Psicología, 2008, 26, 1, 143-148.

U.M.C. (Unidad de Medición de Calidad Educativa). Fundamentación de la Evaluación de Actitudes en la Evaluación Nacional del 2001. Ministerio de Educación de Perú. Recuperado de (www.minedu.gob.pe/umc/2001/doctec/evanac2001_fundamentacion.pdf)

U.M.C. (Unidad de Medición de Calidad Educativa) (2005). Evaluación del rendimiento estudiantil 2004. Lima. Ministerio de Educación.

Van Eerde, W. (2003). A meta-analytically derived nomological network of procrastination. Personality and Individual Differences, 35, 1401- 1418.

Vigil-Colet, A., Lorenzo-Seva, U., y Condon, L. (2008). Development and validation of the statistical anxiety scale. Psicothema, 20(1), 174-186.

Vygotsky, L. S. (1991). A Formação Social da Mente. São Paulo. Martins Fontes.

Zan, R., Brown, L., Evans, J. y Hannula, M.S. (2006). Affect in mathematics education: an introduction. Educational Studies in Mathematics, 63, 113-121.

Zubeidat, I., Fernández-Parra, A., Sierra, C., Salinas, J.M. (2007). Comorbilidad de la ansiedad social específica y generalizada en adolescentes españoles. Psicothema, 19(4), 654-660.