1 Introduction

General-purpose multicore architectures and graphics processor units (GPUs) dominate today’s landscape of high performance computing (HPC), offering unprecedented levels of raw performance when aggregated to build the systems of the Top500 list [ 1]. While the performance-power trade-off of HPC platforms has also enjoyed considerable advances in the past few years [ 2] —mostly due to the deployment of heterogeneous platforms equipped with hardware accelerators (e.g., NVIDIA and AMD graphics processors, Intel Xeon Phi) or the adoption of low-power multicore processors (IBM PowerPC A2, ARM chips, etc.)— much remains to be done from the perspective of energy efficiency. In particular, power consumption has been identified as a key challenge that will have to be confronted to render Exascale systems feasible by 2020 [ 3,  4,  5]. Even if the current progress pace of the performance-power ratio can be maintained (a factor of about 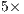in the last 5 years [ 2]), the ambitious goal of yielding a sustained ExaFLOPS (i.e., floating-point arithmetic operations, or flops, per second) for 20–40 MWatts by the end of this decade will be clearly exceeded.

In recent years, a number of HPC prototypes have proposed the use of low-power technology, initially designed for mobile appliances like smart phones and tablets, to deliver high MFLOPS/Watt rates [ 6,  7]. Following this trend, in this paper we investigate the performance, power and energy consumption of two low-power architectures, concretely an Intel Atom and a hybrid system composed of a multicore ARM processor and an NVIDIA 96-core GPU, and a general-purpose multicore processor, using as a workhorse matrix inversion via Gauss-Jordan elimination (GJE) [ 8]. While this operation is key for the solution of important matrix equations arising in control theory via the matrix sign function [ 9,  10], the relevance of this study carries beyond the inversion operation/method or these specific applications. In particular, a blocked implementation of matrix inversion via GJE casts the bulk of the computations in terms of the matrix-matrix product, so that its performance as well as power dissipation and energy consumption are representative for many other dense linear algebra operations such as, e.g., the solution of linear systems, linear-least squares problems, eigenvalue computations, etc.

The rest of the paper is structured as follows. In Section 2 we briefly review matrix inversion via the GJE method and an applications of this particular operation. Specifically, we introduce the sign function, which plays an important role for the resolution of several scientific problems arising in control theory. Next, in Section 3, we describe the specific implementation of the GJE method on the two low-power architectures selected for our study: i) an Intel Atom processor not much different, from the programming point of view, from a mainstream multicore processor like the Intel Xeon or the AMD Opteron; and ii) a hybrid board with ARM+NVIDIA technology that can be viewed as a low-power version of the heterogeneous platforms equipped with hardware accelerators that populate the first positions of the Top500 list. Finally, Sections 4 and 5 contain, respectively, the experimental evaluation and a few concluding remarks resulting from this investigation.

2 Matrix Inversion via GJE and its Applications to Control Theory

The traditional approache to compute a matrix inverse is based on the LU factorization and consist of the following three steps:

1. Compute the LU factorization 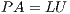, where 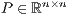is a permutation matrix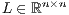, and and 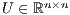are, respectively, unit lower and upper triangular factors [ 11].
2. Invert the triangular factor .
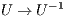3. Solve the system 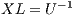for .
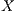4. Undo the permutations .

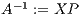An alternative approach to compute a matrix inverse is the GJE, an appealing method for matrix inversion in current architecture, becauase it presents a computational cost and numerical properties analogous to those of traditional approaches  [ 8] but superior performance on a variety of parallel architectures, including clusters [ 12], general-purpose multicore processors and GPUs [ 9].

Figure 1 shows a blocked version of the GJE algorithm for matrix inversion using the FLAME notation. There stands for the number of rows of matrix 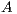 while, for details on the notation, we refer the reader to [ 13,  14]. A description of the unblocked version of GJE, called from inside the blocked routine, can be found in [ 12]; for simplicity, we do not include the application of pivoting during the factorization, but details can be found there as well. Given a square (nonsingular) matrix of size 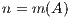, the cost of matrix inversion using this algorithm is 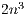flops, performing the inversion in-place so that, upon completion, the entries of 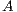are overwritten with those of its inverse.

Figure 1: Blocked algorithm for matrix inversion via GJE without pivoting.

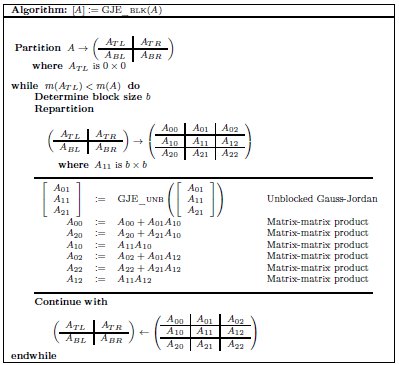
Our primary interest for the GJE matrix inversion method is twofold. First, most of the computations of the blocked algorithm are matrix-matrix products (see Figure 1). Therefore, the conclusions from our power–energy–performance evaluation can be extended to many other dense linear algebra kernels such as the solution of linear systems via the LU and Cholesky factorizations, and least-squares computations using the QR factorization [ 11], among others.

Additionally, explicit matrix inversion is required during the computation of the sign function of a matrix 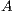using the Newton iteration method [ 10], which we describe brief in the next sub-section.

2.1 Matrix sign function

Consider a matrix 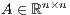with no eigenvalues on the imaginary axis, and let

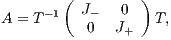(1)

be its Jordan decomposition, where the eigenvalues of 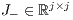and 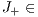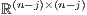have negative and positive real parts [ 11] respectively.

The matrix sign function of 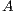is then defined as

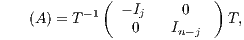(2)

where 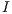denotes the identity matrix of the order indicated by the subscript. The matrix sign function is a useful numerical tool for the solution of control theory problems (model reduction, optimal control) [ 15], and the bottleneck computation in many lattice quantum chromodynamics computations [ 16] and dense linear algebra computations (block diagonalization, eigenspectrum separation) [ 11,  17]. Large-scale problems as those arising, e.g., in control theory often involve matrices of dimension  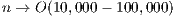[ 18].

There are simple iterative schemes for the computation of the sign function. Among these, the Newton iteration, given by

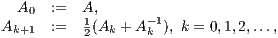(3)

is specially appealing for its simplicity, efficiency, parallel performance, and asymptotic quadratic convergence [ 17,  19,  20]. However, even if 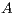is sparse, 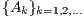are in general full dense matrices and, thus, the scheme in (3) roughly requires 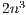floating-point arithmetic operations (flops) per iteration.

3 High Performance Implementation of GJE on Multicore and Manycore Architectures

As previously stated, the GJE algorithm for matrix inversion casts the bulk of the computations in terms of matrix-matrix products; see Figure 1. In particular, provided that the block size 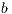is chosen there as 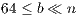, the computational cost of the factorization of the “current” panel , performed inside the routine GJE_UNB, is negligible compared with that of the update of the remaining matrix blocks following that operation.

Therefore, the key to attaining high performance with GJE algorithm primarily relies on using a highly tuned implementation of the matrix-matrix product and, under certain conditions on parallel architectures, the reduction of the serial bottleneck that the factorization of represents applying, e.g., a look-ahead strategy [ 21].

Fortunately, there exist nowadays highly efficient routines for the matrix-matrix multiplication, embedded into mathematical libraries such as Intel MKL, AMD ACML, IBM ESSL, or NVIDIA CUBLAS; but also as part of independent development efforts like GotoBLAS2 [ 22] or OpenBLAS [ 23]. Therefore, for the implementation of GJE in the Atom processor (as well as for the Intel Xeon processor that will be used for reference in the experimental evaluation), we simply leverage the matrix-matrix product kernel sgemm in a recent version of Intel MKL.

Let us consider next the hybrid SECO development kit [ 24], which combines a quad-core NVIDIA Tegra3/ARM Cortex A9 processor and an NVIDIA Quadro 1000M GPU with 96 cores, both processors in single board (see Figure 2).

The properties of the GJE algorithm and the hybrid nature of the target platform ask for an implementation that harnesses the concurrency of the operation while paying special attention to diminish the negative impact of communications between the memory address spaces of the Cortex A9 processor and the Quadro GPU. In a previous work we introduced a CPU-GPU implementation of the GJE algorithm for matrix inversion [ 9], and demonstrated the benefits of mapping each operation to the most convenient device: multicore processor or manycore accelerator. In this work we apply a similar approach to obtain a tuned implementation of the GJE algorithm for the SECO platform. The highly parallel matrix-matrix products are computed in the GPU. On the other hand, the panel factorizations performed with the unblocked algorithm GJE_UNB, which consist of fine grain operations, are computed in the multicore CPU. This algorithm is summarized in Figure 3 (note that, for simplicity, pivoting is ommitted in the figure, though partial column pivoting is performed in all our implementations). The block size is tuned for the architecture and also for each problem dimension.

Additionally, we include a look-ahead technique that allows to overlap the factorization in step 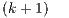with part of the updates performed during iteration 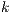, and also keeps a low communication overhead.

Finally, the parallelism intrinsic to the linear algebra operations that appear in algorithms GJE_BLK and GJE_UNB are exploited using parallel implementations of the BLAS. In particular, we employ kernels from libraries CUBLAS and reference BLAS (parallelized with OpenMP directives), for the Quadro GPU and the ARM processor respectively.

Figure 3: Blocked algorithm for matrix inversion via GJE without pivoting in the SECO platform.

4 Evaluation

This section is divided into three parts. First, we introduce the target platforms. This is followed by a description of the power measurement system. Finally, the results obtained are presented and analyzed.

4.1 Hardware platforms

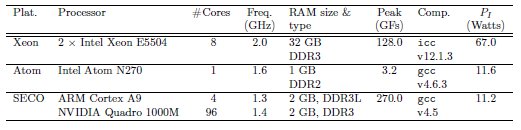
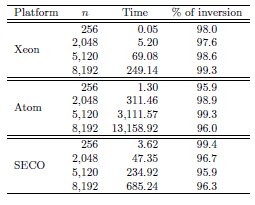
We evaluate the matrix inversion routines on three target hardware platforms: a state-of-the-art server equipped with two multicore Intel Xeon (“Nehalem”) processors, an Intel Atom-based laptop, and a hybrid ARM+NVIDIA board from SECO. Details about the hardware and the compilers employed in each platform can be found in Table 1.

The inversion routines for the Xeon and Atom processors heavily rely on the matrix-matrix product kernel in Intel MKL (versions 10.3 and 11.0, respectively). The hybrid implementation for the SECO platform makes intensive use of the kernels in CUBLAS (version 5.0) and the legacy implementation of BLAS (available at http://www.netlib.org/). parallelized with OpenMP. (We note, however, that the amount of computation that is performed in the cores of the Cortex A9 processor is small, and mostly based on BLAS-1 and BLAS-2 operations, so that we do not expect significant differences if a tuned version of BLAS was used for this architecture.)

The codes were compiled with the -O3 optimization flag and all the computations were performed using single precision arithmetic.

---

Table 1: Architectures employed in the experimental evaluation and the average power dissipation while idle ()

---

4.2 Power measurement

In order to measure power, we connected a WATTSUP?PRO wattmeter (accuracy of 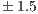% and a rate of 1 sample/sec.) to the power line from the electric socket to the power supply unit (PSU), collecting the results on a separate server. All tests were executed for a minimum of 1 minute, after a warm up period of 2 minutes.

Since some of the platforms where the processors are embedded contain other devices —e.g., disks, network interface cards, and on the Atom laptop even the LCD display— on each platform we calculated the average power while idle for 1 minute, 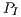, and then used this value to calculate the net energy, corresponding to the consumption after subtracting 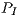from the power samples. We expect this measure allows a fair comparison between the architectures, as in this manner we only evaluate the energy that is necessary to do the actual work.

4.3 Experimental evaluation

The experimental evaluation is performed in two stages. First, we analyze the performance and power-energy consumption of the GJE for matrix inversion algorithm. Next, we study the impact of Gauss-Jordan inversion method on the resolution of matrix sign function.

4.3.1 Matrix inversion

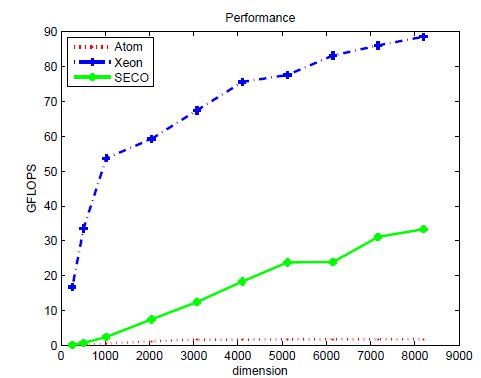
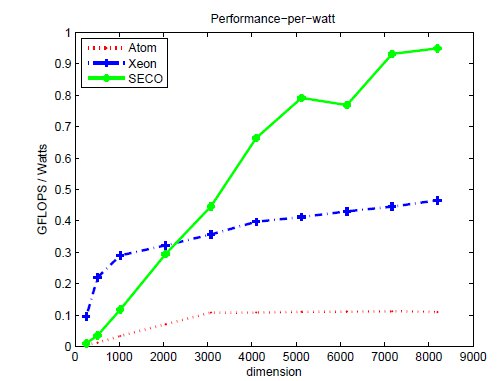
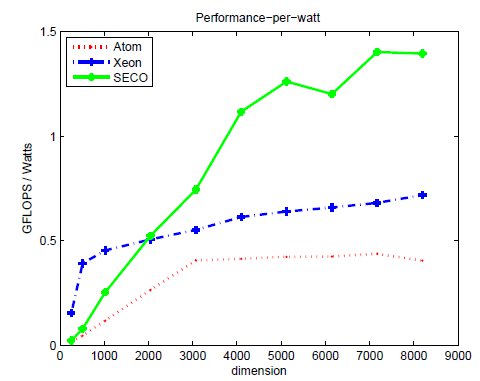
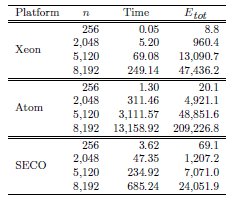
Tables 2, 3 and 4 collect the results obtained from the execution of the different implementations of the GJE matrix inversion algorithm on the three target platforms, for problems of dimension 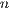varying from 256 to 8,192. The same information is refined and collected graphically, in terms of GFLOPS and GFLOPS/Watt, in Figures 4, 5 and 6.

The results characterize the different performance-power-energy balance of the platforms: The Intel Xeon is considerably faster than the Intel Atom, in factors that range from more than 255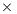 for the smaller problem dimensions, to about 50.8 for the larger ones; but the power dissipated by the Atom architecture is, depending on the problem size, 9.8 to 12.4 lower than that of the Intel Xeon architecture. The outcome of the combination of these two factors is that, from the perspective of total energy, the Intel Atom spends between 4.25 and 22.0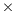 more energy than the Intel Xeon to compute the inverse; but the excess is only between 1.77 and 8.46 if we consider net energy. On the other hand, the SECO board presents quite an interesting balance. While being clearly slower than the Intel Xeon (especially for the smaller problems), this platform also shows a remarkable advantage from the point of view of energy efficiency. Thus, when the problem size is larger than 2,048, the ratios for the total and net energy of these two platforms are, respectively, up to 2.04 and 1.94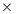 in favor of the SECO system.

---

Table 2: Time (in sec.); GFLOPS; average and maximum power consumption (Pavg and Pmax, respectively, in Watts); and total and net energy (Etot and Enet, respectively, in Joules) in Xeon

---

---

Table 3: Time (in sec.); GFLOPS; average and maximum power consumption (Pavg and Pmax, respectively, in Watts); and total and net energy (Etot and Enet, respectively, in Joules) in Atom

---

---

Table 4: Time (in sec.); GFLOPS; average and maximum power consumption (Pavg and Pmax, respectively, in Watts); and total and net energy (Etot and Enet, respectively, in Joules) in SECO

---

4.3.2 Matrix sign function

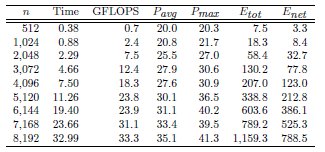
We next evaluate the performance and power-energy consumption to solve the matrix sign function (see Section 2.1) using the three target platforms, i.e. Xeon, Atom and SECO. Concretely, Table 5 presents the runtime to obtain the matrix sign function (in seconds) for four different problem dimensions, 256, 2,048, 5,120 and 8,192. Additionally, we discriminate the execution time related to the matrix inversions including the associated percentage in the overall process time. The time required for different problem dimensions can be easily infered from the results showed in the previous subsection and the data in Table 5. As the input matrices were randomly generated, and do not correspond to a real problem, the number of steps of the algorithm to reach the solution was fixed to 20 iterations.

---

Table 5: Time (in sec.) and percentage of matrix inversion runtime to calculate the matrix sign function

---

The time evaluation summarized in Table 5 shows the close relation between the computational complexity of the matrix sign function algorithm and the matrix inversion kernel. Thus, the time required by the computation of the matrix inverses represents at least the 95% of the computational time of the overall process. This allows to easily compute a rough approximation of the energy consumption from the data obtained during the matrix inversion kernels evaluation. In particular, Table 6 summarizes the total runtime (in seconds) and the energy consumption (in Joules) for the computation of the matrix sign function on the three platforms and four different dimension cases (256, 2,048, 5,120 and 8,192).

---

Table 6: Time (in sec.) and total energy (Etot, in Joules) to calculate the matrix sign function

---

The highest energy consumption is required by Atom. Despite its low average power consumption, the large computational time leads to the worst results in terms of energy for this platform. Thus, the energy consumed by the Xeon is 4 lower for the largest problem tackled. On the other hand the lowest energy consumption is obtained for SECO, which requires 2 and 8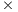 less energy than Xeon and Atom respectively. This is explained by the favorable performance-power ratio of the SECO platform.

5 Concluding Remarks and Future Directions

We have investigated the trade-off between performance and power-energy of three architectures using as a benchmark the matrix sign function, a useful mathematical tool in some numerical methods. In particular, the evaluation includes two low-power architectures and a conventional general-purpose multicore processor.

Our experimental evaluation is divided in two stages. First, the main computational kernel in the sign function algorithm, the general matrix inversion, is evaluated. Then, the complete sign function algorithm is assessed.

The use of blocked routines for GJE matrix inversion shows that, for dense linear algebra operations that are rich in matrix-matrix products, the race-to-idle strategy (i.e, execute the task as fast as possible, even if there is a high power dissipation associated with that) is crucial to attain both high throughput and performance-per-watt rates on general-purpose processor architectures, favoring power-hungry complex designs like the Intel Xeon processor over the Intel Atom counterpart. However, the experimentation also shows that a hybrid architecture that combines a low-power multicore processor and a limited GPU can offer competitive performance compared with that of the Intel Xeon platform, while being clearly superior from the perspective of energy efficiency.

The results obtained during the evaluation of the matrix sign function reinforce the conclussions extracted from the previous analisys.

Future research lines resulting from this experience will include:

• Evaluate in detail the power-energy consumption of each stage of the GJE method for general matrix inversion.
• Analyze the impact of other optimization techniques on memory-bounded dense linear algebra operations, and the adoption of dynamic frequency-voltage scaling (DVFS) and dynamic concurrency throttling (DCT) for certain stages of the algorithm.
• Extend our study to other high performance platforms, e.g. Kepler GPUs connected to high end multi-core CPU and extend the evaluation to other low-power processors with a large number of cores, such as ARM Cortex A15 processors.

Acknowledgments

The researcher from UJI was supported by the CICYT project TIN2011-23283 of the Ministerio de Economía y Competitividad, FEDER, and the EU Project FP7 318793 “EXA2GREEN”. P. Ezzatti acknowledges support from Agencia Nacional de Investigación e Innovación (ANII) and Programa de Desarrollo de las Ciencias Básicas (PEDECIBA), Uruguay. The authors gratefully acknowledge Juan Pablo Silva and Germán León for their technical support with SECO hardware platform.

References