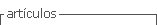Antecedentes y fundamentación teórica
Las estrategias de aprendizaje se valoran como herramientas clave en los procesos de enseñanza-aprendizaje en todas las áreas de conocimiento. Los estudios pioneros relacionaron estas estrategias con el procesamiento cognitivo de la información, lo que permitió la construcción de modelos que ayudaran a comprender el funcionamiento de la cognición humana (Badia, Álvarez, Carretero, Liesa y Becerril, 2012).
Las estrategias se pueden considerar operaciones realizadas por el pensamiento cuando tiene que enfrentarse a la tarea del aprendizaje. En consecuencia, no son meras técnicas de estudio ya que tienen un carácter intencional e implican un plan de acción, mientras que las técnicas son mecánicas y rutinarias (Beltrán, 2003).
El empleo de estrategias de aprendizaje conlleva la puesta en marcha de un aprendizaje estratégico y autónomo basado en el concepto de aprender a aprender y puesto en valor por la Unión Europea (European Commission, 2006). Consecuentemente el meta-aprendizaje es el nexo de unión entre las estrategias de aprendizaje y la autorregulación (Thoutenhoofd y Pirrie, 2015). Es así que en ciertas investigaciones los términos de aprendizaje autorregulado y de estrategias de aprendizaje se emplean indistintamente (Dinsmore, Alexander y Loughlin, 2008). Las similitudes son claras si se define a la autorregulación del aprendizaje como los procesos individuales mediante los cuales el alumnado activa, orienta y mantiene sus pensamientos, afectos y acciones hacia la consecución de objetivos de aprendizaje (Monereo y Badia, 2013).
La implicación educativa de las estrategias de aprendizaje se relaciona con variables psicoinstruccionales como la motivación escolar (Gil-Jaurena, 2012) y el autoconcepto (Núñez-Pérez et al., 1998).
Se han estudiado diversos enfoques y líneas de investigación sobre estrategias de aprendizaje. No obstante, en cuanto a sus implicaciones en el aprendizaje la mayoría coincide en la importancia de fomentar entre el alumnado la formación y desarrollo de estrategias cognitivas, metacognitivas, de autorregulación personal, motivacional y de aprendizaje cooperativo con el fin de incrementar su rendimiento escolar (Pintrich, 1995).
El hecho de que las estrategias de aprendizaje pueden ser un motor de aprendizaje da especial importancia a su clasificación. Quizá sea esta la razón por la que no existe un consenso sobre su configuración dimensional, a lo que habría que añadir su carácter multifacético que hace de las estrategias un constructo difuso en ocasiones.
Con el objetivo de definir las múltiples categorías en las que las estrategias se agrupan, se destacan tres características estrechamente unidas a la conducta humana: el poder, el decidir y el querer (Beltrán, 2003). El poder se asocia con las estrategias cognitivas o de procesamiento de la información, el decidir está vinculado con las estrategias metacognitivas, mientras que el querer se manifiesta en las estrategias afectivo-motivacionales y de apoyo.
Las estrategias en el aprendizaje de las matemáticas
El objetivo mayoritario de las investigaciones sobre estrategias de aprendizaje se ha focalizado en el análisis de la variación del rendimiento académico en función del empleo de las mismas, hecho que se produce en cualquier área o ciclo educativo (Ahmed, van der Werf, Kuyper y Minnaert, 2013; Murayama, Pekrum, Lichtenfeld y vom Hofe, 2013).
Respecto a las relaciones entre las estrategias y el rendimiento en matemáticas, un estudio sobre los resultados del Informe PISA 2003 relata que el empleo de la estrategia de elaboración se incrementa a medida que el nivel de rendimiento aumenta (Thiessen y Blasius, 2008). Asimismo, se ponen en duda las dimensiones establecidas al comprobarse que, al menos en el área de las estrategias de aprendizaje de las matemáticas, el número de dimensiones analizadas varía de una a tres en diversos países en función del nivel de rendimiento en matemáticas.
Un estudio análogo ofrece datos del Informe PISA 2000 (Chiu, Wing-Yin y McBride-Chang, 2007) e informa lo siguiente:
1) El empleo de la estrategia de repetición está relacionado negativamente con el rendimiento en matemáticas, coincidiendo este resultado con las conclusiones obtenidas por otra investigación (Czuchry y Dansereau, 1998) en el sentido de que memorizar constituye una estrategia ineficaz para el aprendizaje de nociones nuevas.
2) La estrategia de elaboración no tiene vinculación con el rendimiento. Este resultado no concuerda con otros estudios realizados anteriormente que relacionan directamente ambas variables, probablemente porque el cuestionario no diferencia adecuadamente entre estrategias de repetición y de elaboración.
3) El uso de estrategias metacognitivas se correlaciona positivamente con el rendimiento en matemáticas.
Otro hilo conductor de investigación que concierne al aprendizaje de las matemáticas y a sus estrategias de aprendizaje se refiere a la intervención en el aula mediante la enseñanza del empleo de dichas estrategias, poniendo el foco en la influencia de la instrucción metacognitiva (Kramarski y Mevarech, 2003; Zamani y Mir, 2011). En cuanto a las estrategias cognitivas, según un estudio realizado con alumnado del último curso de educación primaria (Perels, Dignath y Schmitz, 2009) el entrenamiento en el uso de estrategias de aprendizaje en la clase de matemáticas brinda resultados satisfactorios. Dichos datos se complementan con otro estudio que analiza alumnado de 2.º de la ESO (en el estado español, Educación Secundaria Obligatoria). Se comprueba la mejora de las competencias a través de la formación fuera de la escuela combinando la autorregulación y la resolución de problemas matemáticos (Perels, Gürtler y Schmitz, 2005).
Son escasas las investigaciones referidas a las variaciones del empleo de estrategias de aprendizaje entre sexos. Se informa sobre un uso más asiduo de las mismas por parte de las alumnas (Cleary y Chen, 2009; IE, 2010; Inglés, Martínez-González y García-Fernández, 2013). Por lo mencionado hasta el momento se puede deducir que las estrategias de aprendizaje tienen repercusión en el aula de matemáticas, lo que hace necesaria una correcta medida de su empleo y de su evolución. El objetivo de esta investigación consiste en analizar las diferencias de sexo en el empleo de estrategias en matemáticas por parte de alumnado perteneciente a la Educación Secundaria Obligatoria (ESO).
Método
La investigación previa apunta a la siguiente categorización de las estrategias: estrategias cognitivas, estrategias metacognitivas, estrategias de gestión de los recursos y estrategias motivacionales y afectivas. En este estudio se analizan las tres primeras focalizadas en el aprendizaje de las matemáticas.
Muestra
Participan 631 estudiantes de tres cursos de Educación Secundaria Obligatoria (ESO): 2.º (13-14 años, 32%), 3.º (14-15 años, 37%) y 4.º (15-16 años, 31%) de los cuales 336 (53.3%) eran mujeres y 295 (46.7%) varones. Por motivos de errores u omisiones en las respuestas a los cuestionarios la muestra final quedó reducida a 565 sujetos. La recolección de datos se ha realizado en 8 centros educativos que pertenecen a la Comunidad Autónoma Vasca, integrantes tanto de la red pública (5) como de la red privada concertada (3). Tras contactar con varios centros finalmente se seleccionan aquellos que responden positivamente a la oferta de participación, por lo que se trata de una muestra de conveniencia.
En la Tabla 1 se expone la distribución de la muestra en función del curso académico y del sexo.
Instrumentos
Para la medida de las estrategias de aprendizaje del alumnado se han propuesto 25 ítems (ver anexo). El cuestionario se basa en una versión para enseñanza secundaria del MSLQ (Motivated Strategies for Learning Questionnaire) (Pintrich, Smith, Garcia y McKeachie, 1991, 1993) adaptada por Berger y Karabenick (2011) para ajustarse al estudio de las matemáticas
La versión original en lengua inglesa ofrece una consistencia interna del cuestionario con valores entre .58 y .86 en la ro de Raykov (Berger y Karabenick, 2011) en una investigación realizada con 306 sujetos del curso equivalente a 3.º de la ESO (9.º grado). Asimismo, las propiedades psicométricas confirmaron una estructura hexafactorial ofreciendo el análisis factorial confirmatorio un índice CFI de .88 (los valores óptimos deben estar en el intervalo entre .90 y 1.00). Esta distribución, de 33 ítems en total, está compuesta por tres escalas de medida para las estrategias cognitivas (repetición, organización y elaboración), una escala para medir las estrategias metacognitivas y dos escalas contextuales (el manejo del tiempo-espacio de estudio y los recursos de ayuda). No obstante, el cuestionario empleado en este estudio (Gasco-Txabarri, Ros y Goñi, 2017) se ajusta a una estructura heptafactorial formada por las mismas escalas del original pero dividiendo la escala de estrategias metacognitivas en dos: planificación y seguimiento-regulación. Asimismo los autores proponen la revisión/reformulación/eliminación de 8 de sus ítems. En consecuencia, esta investigación suprime los ítems indicados formando un total de 25.
Los ítems fueron elaborados en base a una escala Likert de cinco puntos. A continuación se concreta la configuración de la citada versión castellana (tres dimensiones divididas en escalas):
Estrategias cognitivas
Repetición (3 ítems). Se miden las estrategias para aprender por repetición. Por ejemplo: “Para estudiar matemáticas repito varias veces las fórmulas o definiciones con el fin de memorizarlas”.
Organización (2 ítems). Se tienen en cuenta las maneras de gestionar los aprendizajes matemáticos. Por ejemplo: “Estudio matemáticas haciendo diagramas, cuadros o tablas para organizar lo que he aprendido”.
Elaboración (2 ítems). Por una parte se mide cómo se relaciona el aprendizaje en matemáticas con otras materias y por otra la transformación de los conceptos matemáticos para una mejor comprensión personal. Por ejemplo: “Cuando estudio matemáticas intento relacionar lo nuevo con lo que ya sé”.
Estrategias metacognitivas
Se distribuyen de la siguiente forma: la planificación y el seguimiento-regulación.
Planificación (5 ítems). Se recopila información sobre cómo se planifican los estudios. Por ejemplo: “Antes de empezar a estudiar matemáticas planeo qué y cómo voy a hacerlo”.
Seguimiento (4 ítems). Contiene ítems relativos a la conciencia, conocimiento y control que tiene el educando sobre su propia cognición. Por ejemplo: “Cuando estudio matemáticas llevo un control de lo que he aprendido”.
Regulación (3 ítems). Se refiere a la habilidad para controlar el esfuerzo y la atención frente a las distracciones o ante tareas difíciles. Por ejemplo: “Si tengo dificultades para resolver un problema, intento otras formas para resolverlo”.
Estrategias contextuales y de gestión de recursos
Recursos de ayuda (3 ítems). Mide a quién o a qué se recurre en caso de dificultad en el aprendizaje. Por ejemplo:”Si no entiendo algo en matemáticas pido ayuda a otros estudiantes”.
Entorno de estudio-tiempo de estudio (3 ítems). Se refiere a las costumbres de estudio en cuanto a espacio y horario. Por ejemplo: ”Estudio matemáticas en un entorno en el que puedo concentrarme”.
Procedimiento
Para comenzar con la recolección de datos se solicita una cita con la dirección de cada centro elegido. Posteriormente se expone tanto la naturaleza de la investigación como las pruebas propuestas al profesorado de matemáticas de 2.º, 3.º y 4.º grados de la ESO.
Se está presente en el momento de la administración de la prueba. Previo al comienzo de la misma se les advierte que la prueba es anónima y que los datos personales que se requieren son, exclusivamente, la fecha de nacimiento y el sexo. Asimismo se informa que los resultados obtenidos no influirán en la calificación escolar.
En promedio la prueba tiene una duración de entre 10 y 15 minutos.
Análisis de datos
Se realiza el análisis factorial exploratorio que permite comprobar la pertenencia de cada ítem a su escala correspondiente. Seguidamente se mide la consistencia interna de las escalas mediante el α de Cronbach.
Para analizar las diferencias entre sexos se implementa la prueba no paramétrica para dos muestras independientes U de Mann-Whitney. La razón de la elección de dicho test no paramétrico es que los datos recogidos no cumplen los criterios ni de normalidad ni de homocedasticidad. Para estimar la magnitud de las diferencias se ha calculado el tamaño del efecto (effect size), denotado por el parámetro r. La interpretación del coeficiente es la siguiente: r=.10, tamaño del efecto débil; r=.30, tamaño del efecto moderado, y a partir de r=.50, tamaño del efecto fuerte (r toma valores entre 0 y 1) (Field, 2009).
El análisis de dichos datos se ha efectuado empleando el software estadístico PASW Statistics 18.
Resultados
Los resultados obtenidos en la presente investigación se clasifican en dos apartados: el análisis factorial exploratorio de las escalas del cuestionario y el análisis de las diferencias en función del sexo.
Análisis factorial exploratorio
Se procede a realizar el análisis factorial exploratorio. Las correlaciones entre las escalas son positivas aunque algunas no lo suficientemente altas (r<.40), por lo que se decide efectuar el análisis de componentes principales con rotación equamax. El índice KMO=.96 es suficiente y la prueba de esfericidad de Bartlett muestra que la relación entre escalas es significativa. Los siete factores explican el 71.74 % de la varianza. Los datos se presentan en la Tabla 2.
Tabla 2: Análisis factorial exploratorio

R: Repetición; O: Organización; El: Elaboración; Pl: Planificación; Se: Seguimiento; Re: Regulación; En: Entorno-tiempo de estudio; Ay: Recursos de ayuda
Los resultados del análisis factorial exploratorio revelan una estructura de siete escalas o factores: tres estrategias cognitivas (repetición, organización y elaboración), dos metacognitivas (planificación y seguimiento-regulación) y dos contextuales y de gestión de recursos (entorno-tiempo de estudio y recursos de ayuda).
La consistencia interna de las escalas, medida empleando el α de Cronbach, resulta aceptable. Todas ellas presentan fiabilidades suficientes, iguales o superiores a .70: repetición (α=.71), organización (α=.73), elaboración (α=.80), planificación (α=.86), seguimiento-regulación (α=.92), entorno-tiempo de estudio (α=.70) y recursos de ayuda (α=.70).
Diferencias en función del sexo
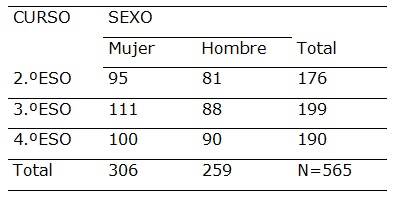
En la Tabla 3 se presentan los resultados asociados a las diferencias en el empleo de estrategias entre alumnas y alumnos en el aprendizaje de las matemáticas. Para ello se implementa el test U de Mann-Whitney:
Según estos datos existen diferencias estadísticamente significativas en el uso de estrategias de aprendizaje en la organización y los recursos de ayuda asociados al género. Las mujeres obtienen puntuaciones superiores a los hombres en dichas escalas lo que significa que las alumnas tienen tendencia a gestionar mejor los saberes matemáticos y a pedir ayuda en mayor medida que los varones. En todo caso el tamaño del efecto de la diferencia hallada es débil (r=.10).
En lo que respecta a la ausencia de diferencias, estos resultados indican un empleo similar de alumnos y alumnas en las demás estrategias:
La repetición o memorización;
La estrategia cognitiva de elaboración que mide cómo se relaciona el saber matemático con otras materias además de la transformación que se realiza de los conceptos matemáticos para una mejor comprensión de los mismos;
La planificación y el seguimiento-regulación, ambas estrategias metacognitivas que miden la preparación, el control y el conocimiento que tiene el alumnado sobre su propia cognición, y;
El entorno de estudio que evalúa el ambiente elegido para estudiar.
Discusión y conclusiones
Los resultados obtenidos con respecto de las diferencias en el empleo de las estrategias de aprendizaje en función del género arrojan datos significativos. Las estrategias de recursos de ayuda y de organización son las únicas que presentan variaciones estadísticamente significativas en favor de las mujeres, a pesar de que la relevancia sea débil (r=.10).
Por una parte, estos datos son coherentes con el supuesto de que las mujeres solicitan más ayuda que los varones en caso de dificultad en el aprendizaje de las matemáticas. De hecho, Cleary y Chen (2009) constatan un mayor requerimiento de ayuda en la materia de matemáticas por parte de las chicas en la transición del último curso de Educación Primaria al primero de Secundaria. Núñez et al. (1998) llegan a la misma conclusión en ciclos educativos muy similares. Asimismo, ciertas investigaciones en la etapa universitaria confirman un resultado similar (Virtanen y Nevgi, 2010).
Por otra parte, un mayor empleo de la organización se asocia a la acción de llevar un mayor orden en el aprendizaje matemático mediante subrayados o esquemas. Para Schiefele (1991) representa una estrategia superficial de procesamiento, mientras que Linnenbrinck y Pintrich (2003)la consideran una estrategia de orden superior.
No se han hallado diferencias en la metacognición a favor de las alumnas, en consonancia con las evidencias aportadas por Núñez et al. (1998). Este hecho supone que las alumnas y alumnos de 2.º, 3.º y 4.º de la ESO presentan un nivel semejante de gestión de su conocimiento matemático en el momento de planificar su aprendizaje, autoevaluarse y regular las dificultades en las que se ven inmersos. Dicha paridad no concuerda con otras investigaciones cotejadas al respecto. Zimmerman y Martínez-Pons (1990) relatan un mayor empleo por parte de las mujeres de estrategias metacognitivas de planificación y control sobre el propio aprendizaje. En este caso, los cursos examinados corresponden a 5.º de primaria, 2.º de la ESO y 1.º de bachillerato y se obtienen en un contexto en el que se evalúa la competencia matemática. Inglés et al. (2013) lo confirman en todo el ciclo de la ESO. En este mismo sentido Rodríguez (2005) informa que las alumnas de la ESO utilizan en mayor medida estrategias cognitivas y metacognitivas de estudio vinculándolas a un aprendizaje significativo y autorregulado.
Análogamente, Bidjerano (2005) verifica una mayor planificación del aprendizaje y autocontrol por parte de las alumnas en educación secundaria, ambas estrategias estrechamente relacionadas con la metacognición. Asimismo, encuentra diferencias en la misma dirección en las estrategias cognitivas de repetición y elaboración. El informe PISA 2009 (IE, 2010) analiza el empleo de tres estrategias de aprendizaje en alumnado de 4.º de la ESO por géneros. Se concluye que son las alumnas las que emplean en mayor medida las estrategias de control tanto en el Estado Español como en la mayoría de los países restantes estudiados. El control o seguimiento forma parte de una de las tres categorías medidas en la metacognición en el presente estudio. No se encuentran diferencias en las estrategias cognitivas de repetición y elaboración. Dicho informe resulta especialmente relevante dada la magnitud de la muestra, a pesar de que ofrezca información de un solo curso.
Por lo expuesto hasta el momento se podría afirmar que las estrategias de aprendizaje en la enseñanza-aprendizaje de las matemáticas han sido investigadas y en ciertos casos aplicadas en el aula con el fin de mejorar el rendimiento del alumnado. No obstante, los resultados comparativos entre cursos y géneros son escasos e, incluso, en ocasiones, contradictorios. Se requiere, por tanto, profundizar en el estudio del empleo de las estrategias de aprendizaje y en su incidencia en la mejora de las competencias matemáticas en educación secundaria, más allá del rendimiento. Estudios futuros de las posibles diferencias según el género darían información sobre la igualdad o la ausencia de ellas en las aulas. Las escasas diferencias encontradas en esta investigación parecen indicar una buena dirección en este sentido.
Conviene mencionar las limitaciones del estudio. La propia aplicación del cuestionario quizá distorsione parcialmente los resultados obtenidos. Los datos concernientes al empleo de estrategias de aprendizaje han sido recopilados mediante autoinforme, con los consiguientes riesgos que esto supone para la credibilidad de aquellos. Asimismo, el hecho de que la muestra sea de conveniencia puede sesgar el sentido de los resultados. De igual manera, se estima importante replicar el cuestionario para así poder implementarlo en una muestra más extensa. Esta réplica podría ayudar a apuntalar la consistencia de las escalas además de contribuir a certificar la idoneidad de su validez en el sistema educativo estatal o internacional.
En un futuro podrían plantearse entrevistas personales y/u observación de acciones concretas en el aula con el fin de conocer más estrechamente la influencia de las estrategias de aprendizaje. Como complemento al diagnóstico sería interesante estudiar las incipientes líneas de investigación abiertas en lo que respecta al entrenamiento de estrategias en el aula para después aplicarlas en las clases de matemáticas.