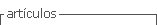Introducción

Desde su nacimiento, la Didáctica de la Matemática (DM) ha sido interpretada, con una visión clásica, como aquella que proporciona las estrategias de enseñanza para las matemáticas, con referentes de actuación para que profesores puedan aplicar en sus aulas y con estrategias de aprendizaje para facilitar al alumno la adquisición del contenido matemático. Desde hace un par de décadas, investigadores como ^{Gascón (1998}), ^{Rico y Sierra (2000}) y ^{Godino (2010}) señalan que la disciplina suele confundirse con una formación pedagógica generalista sin atribuirle un contenido específico basado en el dominio del propio campo disciplinar. Se le reduce a “capítulos” o enfoques particulares y a meros conocimientos técnicos, que pertenecen al ámbito de la didáctica general, pedagogía o a la psicología de la educación, además de concebir a la didáctica y a la matemática como elementos disjuntos y no como una unidad con carácter propio.

Es importante mencionar que esta visión sobre la DM prevalece fuertemente en el ámbito escolar y se amplía a las didácticas específicas (didáctica del álgebra, didáctica del cálculo, etcétera), en las que se supone que el aprendizaje depende solo del grado en que el profesor domina el arte de enseñar y, al mismo tiempo, de la voluntad y la capacidad de los alumnos para dejarse moldear por el artista (^{Gascón, 1998}).

Aunque internacionalmente la disciplina es actualmente reconocida y situada como orientadora de los procesos de aprendizaje y de enseñanza de las matemáticas, así como de sus agentes intervinientes (profesor, alumno, institución, currículo), en México aún perdura la visión clásica. Estudios evidencian que, en el contexto mexicano, la investigación y la formación del profesorado (inicial y continua), así como el desarrollo profesional docente no tienen aristas comunes, por lo que el conocimiento del profesor respecto a su práctica educativa no está consolidado (^{Parada, Figueras y Pluvinage, 2009}; ^{Dolores, 2013}). Esto ha imposibilitado la apreciación de la disciplina como elemento orientador, no solo para el profesorado y su formación, sino para la actuación docente, así como para el diseño y selección de tareas y actividades.

De esta manera, e independientemente de la diversidad de teorías y propuestas metodológicas que han surgido desde la DM, este artículo se propone considerar el diseño de tareas profesionales articuladas desde la investigación como una ruta de aprendizaje durante la formación de profesores. Así nos aproximamos a abordar la cuestión: ¿qué tipo de tareas profesionales precisan plantearse durante la formación del profesorado para llevar a cabo su práctica educativa? Esta pregunta ha surgido de reflexiones previas surgidas del considerar la influencia de las tareas en la formación de los profesores en otros estudios (ver ^{Aké, 2019}; ^{López-Mojica y Aké 2019}; ^{Graciano y Aké, 2017}).

Bajo esta premisa, en el siguiente apartado se contextualiza la realidad de la formación de profesores de matemáticas en México. A continuación, se mencionan algunos aportes teóricos realizados desde la investigación para la formación docente. Más adelante, se toma una postura específica para el planteamiento de las tareas profesionales, se describe el diseño de las tareas y una propuesta de implementación para el aula. En el penúltimo apartado se desarrollan las tareas profesionales, utilizando como ejemplo la enseñanza de los productos notables, y se concluye con el planteo de algunas consideraciones finales.

La formación de profesores de matemáticas en México

La formación didáctica (y matemática) del profesorado que atiende a los estudiantes de primaria (6-12 años), de secundaria (13-15 años) y de bachillerato (16-18 años) es uno de los ámbitos de actuación de la educación matemática con más variedad de problemas y, por tanto, con mayor potencialidad para la investigación y para el desarrollo y consolidación de la Didáctica de la Matemática (^{Rico, Sierra y Castro, 2002}). De hecho, la formación del profesorado en esta disciplina es uno de los campos de estudio más amplios de la DM. Sin embargo, pese a los avances en las investigaciones sobre el conocimiento que debiera tener el profesor (Hill, ^{Ball y Schilling, 2008}; ^{Godino, 2009}; ^{Dolores, García-González, Hernández-Sánchez y Sosa, 2013}) aún no está esclarecida la naturaleza del tipo de formación de aquellos que desean ejercer la docencia en matemáticas. Por ejemplo, en el contexto europeo, para que los profesores de matemáticas puedan desempeñarse como tales se sugiere la existencia de una doble formación: la científica -recibida en las facultades y por tanto de especialización en una materia de estudio- y, luego de esta, la especializada, que se trata de un curso breve de carácter pedagógico que ofrecen las facultades de Educación (^{Vega-Gil, 2005}).

En México, la formación de profesores de matemáticas es compleja, tal como lo expone ^{Dolores et al. (2013}) en su obra Matemática Educativa: La formación de profesores, en la que exhiben el distanciamiento que existe entre la formación propuesta en los currículos oficiales y la que se sugiere desde la investigación, considerando el punto de vista teórico y metodológico.

En dicha obra se identifican dos panoramas que caracterizan la realidad formativa del docente de matemáticas. El primer panorama indica que existe una pluralidad formativa. Al respecto ^{Dolores y Hernández-Sánchez (2013}) señalan que la formación de profesores para preescolar, primaria y secundaria es atendida por la Escuela Normal para Maestros. Por otro lado, la demanda de profesores de matemáticas para el bachillerato ha sido cubierta por profesionales egresados de las universidades o centros de educación superior, no necesariamente formados como profesores de matemáticas. Más bien son ingenieros, matemáticos, contadores, actuarios u otros profesionales que se hacen profesores de matemáticas en la práctica. Así, los maestros de preescolar y de primaria tienen una formación generalista como licenciados e imparten diversas áreas del conocimiento incluyendo el aspecto matemático. Los profesores de secundaria tienen líneas terminales de formación, es decir, obtienen una licenciatura de maestro en educación secundaria especializado en matemáticas. El trabajo del docente de matemáticas para el bachillerato, a diferencia del contexto normalista, no cuenta con una formación profesional específica.

El segundo panorama es el hecho de que contar con una formación adicional a los estudios de licenciatura es opcional en el caso de ejercer la docencia. Esto ha motivado que diferentes universidades del país oferten carreras universitarias tendientes a la formación de profesores, denominadas como licenciaturas en enseñanza de las matemáticas, educación matemática o matemática educativa, entre otras (^{Dolores, 2013}; ^{Dolores y Hernández-Sánchez, 2013}). En este sentido, se han identificado tensiones entre los aspectos puramente matemáticos y los aspectos didácticos y pedagógicos a considerar en dicha formación, sobre todo de quienes deben estar a cargo de esta formación (formadores de profesores).

Ambos panoramas reflejan premisas diferentes respecto a los requerimientos para la formación del profesor de matemáticas. En este marco, ^{Rico y Sierra (2000}) plantean cuestiones como: ¿qué componentes básicos constituyen el necesario conocimiento disciplinar y didáctico para un profesor de matemáticas?, ¿cuántos y qué campos de las matemáticas debe conocer un profesor?, ¿cómo se estructura el conocimiento curricular del profesor en formación?, ¿cómo puede mejorarse el conocimiento profesional del profesor en activo?, ¿cómo promover el trabajo en equipo para la planificación y el diseño?, ¿qué destrezas son necesarias para la gestión de un aula de matemáticas?, ¿cómo adquiere formación práctica el profesor de matemáticas? Son cuestiones que aún están abiertas, pero desde la Didáctica de la Matemática es posible establecer pautas de actuación para abordarlas, sin esperar la producción de situaciones didácticas modélicas que el profesor debe imitar (^{Godino, 2010}), sino más bien proporcionarle las herramientas para propiciar la construcción del conocimiento matemático en el aula.

Ante la gran brecha entre la investigación y la docencia -dada porque los docentes son ajenos a las investigaciones que tratan sobre ellos mismos, sus concepciones y representaciones, sus modos de acción y de decisión, sus conocimientos y competencias (^{Artigue, 2004})- se plantea como alternativa que la DM sirva como orientadora para guiar y establecer no solo un currículo para la formación de profesores de matemáticas, sino también una fuente de información para que profesores en formación y en activo mejoren su práctica docente y se reduzca así la mencionada brecha. Por tal motivo, es importante que el profesorado de matemáticas identifique a la disciplina como aquella que puede aportar conocimientos sobre su propia formación, sobre los errores y dificultades de los estudiantes y su tratamiento en el aula, el desarrollo histórico de la matemática, la diferencia entre la matemática de los matemáticos, la matemática escolar y la actividad matemática escolar de los estudiantes. Tal como menciona Artigue (2004):

La investigación (en Didáctica de la Matemática) puede y debe ayudarnos a pensar, ayudarnos a desconfiar de las soluciones ingenuas y tentadoras, ayudarnos para tener en cuenta la medida de la complejidad de los problemas que debemos administrar, proponernos senderos, a la vez ambiciosos y realistas, para abordarlos, ayudarnos a acompañar las acciones y a evaluar sus efectos (p. 26).

Interpretarla de esta manera puede ayudar a modificar la formación docente de la siguiente manera (^{Brousseau, 1990},¹⁹⁹¹):

Se precisa establecer sinergias que permitan la incidencia de esta disciplina, tanto para formar a los profesionales de la enseñanza de las matemáticas como para orientar la práctica docente en el aula. Es en este sentido que se postulan a las tareas profesionales como un punto de inflexión para conectar los resultados de las investigaciones con la docencia, a través de la formación de profesores.

La formación de profesores de matemáticas a través de los modelos de conocimiento

Uno de los aportes a la formación docente en matemáticas desde las investigaciones son los modelos de conocimiento del profesor. Estos modelos reconocen que el conocimiento matemático y didáctico requerido para la enseñanza de las matemáticas es de tipo específico (^{Ponte y Chapman, 2008}, ²⁰¹⁶) por lo que proponen caracterizarlos como una integración de diferentes dominios del conocimiento (^{Llinares, 1998}). Uno de los primeros constructos articulados fue la propuesta de Shulman de “conocimiento de contenido y conocimiento pedagógico del contenido”, que son referentes para la mayoría de los estudios sobre el conocimiento del profesor (^{Shulman, 1986}). El “conocimiento matemático profundo” (^{Hossin, Mendrick y Adler, 2013}) es otra postura que señala la necesidad de un vasto conocimiento de las matemáticas a enseñar. Por otra parte, en la perspectiva del “cuarteto del conocimiento” (^{Rowland, Huckstep y Thwaites, 2005}), el conocimiento y las creencias evidenciadas en la enseñanza de las matemáticas pueden ser vistas a partir de cuatro dimensiones: fundamento, transformación, conexión y contingencia. Con el uso creciente de la tecnología en las aulas, se propuso el “conocimiento tecnológico pedagógico del contenido” (^{Koehler y Mishra, 2009}). Otros referentes teóricos que han emergido son la noción de “proficiencia” en la enseñanza de las matemáticas (^{Schoenfeld y Kilpatrick, 2008}) y la noción de “profesor de matemáticas reflexivo” y “reflexión sobre la práctica” (^{Schön, 1983}).

Pese a las diversas investigaciones sobre la formación docente y los diferentes estudios realizados bajo los diferentes modelos del conocimiento, aún no existe un marco común. En este sentido, ^{Wu (2018}) afirma que mientras no se encuentre un marco teórico-metodológico homogéneo para desarrollar en los profesores el conocimiento del contenido que necesitan para lograr un nivel de competencia en la enseñanza de las matemáticas, no se puede hablar de programas de formación (aunque estos existan). Actualmente se desarrollan propuestas que pretenden integrar los diferentes dominios del conocimiento para el profesor, como es el caso del “conocimiento y competencia didáctico-matemático” (^{Godino, Giacomone, Batanero y Font, 2017}) o el trabajo de ^{Montes, Contreras y Carrillo (2013}) con su “modelo de conocimiento especializado del profesor de matemáticas”.

Lo previo representa un avance en la delimitación y definición de estos conocimientos y su naturaleza. Sin embargo, las propuestas están fundamentadas en supuestos teóricos y metodológicos diferentes, en los que es posible encontrar coincidencias, pero también diferencias entre los modelos. Esto ha desembocado en la diversidad de los elementos formativos de los profesores.

Más allá de buscar y proponer una formación homogénea para el profesorado, la intención es comenzar a integrar estos elementos a la docencia, dada la evidencia de su desvinculación. En este sentido, ^{Dolores (2013}) y ^{Hernández, Sosa y López (2013}) mencionan que, aunque existen investigaciones realizadas en el área de la formación del profesorado de matemáticas, las propuestas no son consideradas para la elaboración de planes de estudios de las licenciaturas y posgrados orientadas a la formación de profesores.

De esta manera, se considera que una vía para alcanzar una vinculación es el planteamiento de tareas profesionales cuya naturaleza esté fundamentada en situaciones relacionadas a la práctica y guiadas teóricamente por los resultados de las investigaciones. Para realizar una propuesta se considera un esquema general de tres componentes que guíen la articulación de tareas profesionales basada en situaciones: un referente teórico, una lógica de desarrollo durante el proceso de instrucción y el estudio de un contenido matemático desde las investigaciones.

Propuesta para el diseño e implementación de tareas profesionales

Desde las contribuciones realizadas por los modelos de conocimiento del profesor, se toma como referente teórico el Conocimiento Matemático para la Enseñanza (Mathematical Knowledge for Teaching o MKT) para proponer tareas profesionales basadas en situaciones. Este modelo es ampliamente utilizado en todo el mundo y ha sido referente para formular y ampliar otros modelos. El MKT propuesto por ^{Hill et al. (2008}) plantea seis elementos del conocimiento de los profesores de matemáticas que se clasifican entre el conocimiento del contenido matemático (conocimiento común del contenido; conocimiento en el horizonte matemático; conocimiento especializado del contenido) y el conocimiento pedagógico de dicho contenido (conocimiento del contenido y los estudiantes; conocimiento del contenido y la enseñanza; conocimiento curricular). A continuación se describen los dominios de conocimiento que se utilizaron para la propuesta de las tareas profesionales:

Las tareas profesionales se plantean de acuerdo con una postura teórica determinada, en este caso se considera al modelo MKT. De esta manera, la intención didáctica de las tareas profesionales está orientada por dicho modelo que permite promover un desarrollo del conocimiento matemático y didáctico en el profesor. Cada tarea profesional puede tener una o varias situaciones concatenadas y relacionadas por la misma intención didáctica. Las situaciones se diseñan a partir de un contenido matemático específico utilizando escenarios que pueden surgir en el aula.

Se establece la lógica de implementación durante el proceso de instrucción para cada una de las tareas profesionales: Figura 1

Figura 1: Fuente: Lógica de implementación de las tareas profesionales  

En la fase inicial se plantean las tareas profesionales integradas por situaciones. Durante la fase individual de la tarea profesional, se discute cada una de las situaciones y se responde a las cuestiones planteadas y estructuradas a partir del referente teórico. En la fase grupal, se realiza una discusión sobre las preguntas planteadas y, en la fase teórica, también se presentan cuestiones que apoyen la vinculación de las investigaciones desarrolladas sobre el contenido matemático con la realidad docente.

Así, para cada tarea profesional se propone una lectura en el marco de las pesquisas. La selección de la lectura depende de las tareas profesionales planteadas y de su intención didáctica. Su incorporación obedece a la consideración del binomio teoría-práctica en la formación del profesorado (^{Sfard, 2001}). En la fase de reajuste se analizan las interpretaciones emergidas en fases previas con la finalidad de confrontarlas con lo que desde la investigación se propone. La fase de institucionalización queda a cargo del formador de profesores; en esta fase se retroalimentan cada una de las demás.

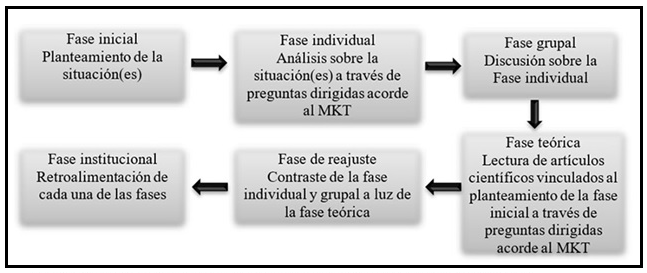
La adopción de una postura teórica estructura la intención didáctica de las tareas profesionales, es decir, los conocimientos que se pretenden desarrollar en los profesores con dichas tareas. La lógica de implementación guía el proceso formativo. El trabajo con un contenido matemático específico y su estudio desde la investigación vinculan problemáticas particulares de ese contenido matemático con el tratamiento de dichas problemáticas desde las investigaciones (Figura 2).

Figura 2: Fuente: Elementos que integran el diseño y la implementación de las tareas profesionales  

Para concretar las tareas profesionales se precisa fijar un contenido matemático; en este caso, se trabaja con el contenido matemático de los productos notables y se proponen dos tareas profesionales integradas por situaciones (Figura 3).

Figura 3: Fuente: Las tareas profesionales propuestas 

Cada situación incluye cuestiones o indicaciones para los profesores, que se vinculan con el desarrollo de tres dominios de conocimiento previamente descritos del MKT (Tabla 1). Resulta importante conectar el referente teórico con las situaciones que se plantean en cada tarea profesional.

Tabla 1: Conocimiento matemático para la enseñanza presentes en las tareas profesionales 

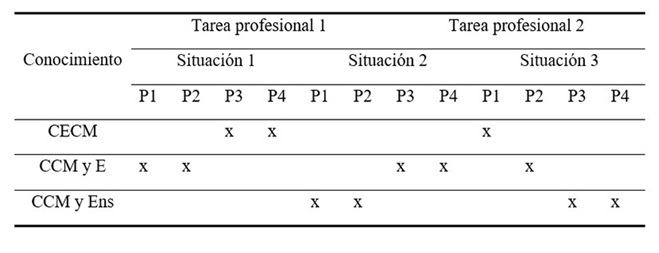
^Fuente: Elaboración propia

A continuación, se detalla el proceso de implementación de estas tareas profesionales utilizando una lógica hipotética de desarrollo.

Tareas profesionales propuestas para la formación de profesores de matemáticas

La investigación en Didáctica de la Matemática permite reflexionar sobre la actuación docente en relación con el tipo de tareas que son puestas en aula con sus estudiantes. Sin embargo, resulta sustancial ofrecer al profesorado de matemáticas durante su formación (y formación continua) escenarios de análisis que permitan articular líneas de actuación para el tratamiento de tópicos matemáticos específicos. Situemos un ejemplo con los productos notables.

Los productos notables, como toda identidad algebraica, están compuestos por dos expresiones equivalentes que difieren exclusivamente en su forma o estructura, por lo que a cada uno le corresponde una factorización que nos regresa del resultado de la multiplicación de los binomios a la representación en factores (^{Vega, 2010}), como a continuación se aprecia:

Cada uno de los citados productos notables genera en los alumnos dificultades de distinta naturaleza (^{Abrate, Pochulu y Vargas, 2006}), tales como:

Una de las posibles causas de estos errores es que, en la enseñanza del tema, los profesores comúnmente lo abordan de forma mecánica, exigiendo solo la memorización y no la comprensión del contenido (^{Acevedo, 2007}), como por ejemplo la igualdad de expresiones algebraicas. Para afrontar estos escenarios complejos de la enseñanza y el aprendizaje de los productos notables, se precisa proporcionar al profesorado de matemáticas -durante su formación y como parte de su conocimiento específico profesional (^{Ponte, 2012})- elementos que le permitan afrontar y superar las dificultades que emergen durante la enseñanza, pero que a su vez le permitan propiciar un aprendizaje en sus estudiantes.

A continuación, se utiliza el contenido matemático de productos notables para desarrollar un planteamiento para el trabajo con profesores, que puede ser desarrollado en su formación inicial o continua. Se pretende incidir en los aspectos del conocimiento especializado del contenido, de un conocimiento del contenido matemático y los estudiantes, así como de la enseñanza, elementos del modelo MKT (^{Ball, Thames y Phelps, 2008}).

El interés por contextualizar los productos notables en la formación de profesores radica en proponer tareas profesionales que involucren situaciones que puedan ayudarlos a superar la diversidad de errores que confrontan con sus estudiantes al trabajar con dicho contenido matemático. Esta es la intención didáctica orientada a partir del desarrollo del conocimiento matemático para la enseñanza que propone el MKT. La implementación de estas tareas seguiría el trayecto de las fases: inicial, individual, grupal, teórica, de ajuste, de retroalimentación. Lo previo ayudaría a superar la percepción del profesor sobre que su formación sea demasiado teórica y distanciada de la realidad, por lo que conocer las implicaciones de la labor docente en su contexto áulico es fundamental en los programas de formación (^{Sánchez y Jara, 2016}).

De esta manera, a través de las tareas profesionales que contienen situaciones erróneas al resolver productos notables, se pretende que el docente de matemáticas en formación argumente con fundamento, desde los aportes de las investigaciones, la toma de decisiones respecto a las situaciones que se le plantean. Las dos primeras situaciones expresan errores que cometen los estudiantes al momento de trabajar con los productos notables, mientras que la última refiere al abordaje de este tema utilizando su aspecto geométrico. Además, se añade una serie de preguntas dirigidas con las que el futuro docente de matemáticas puede analizar la naturaleza del error, al mismo tiempo que centra su atención sobre las posibles causas y estrategias para su tratamiento en el aula utilizando investigaciones realizadas desde la Didáctica de la Matemática.

Tarea profesional 1. Análisis de errores

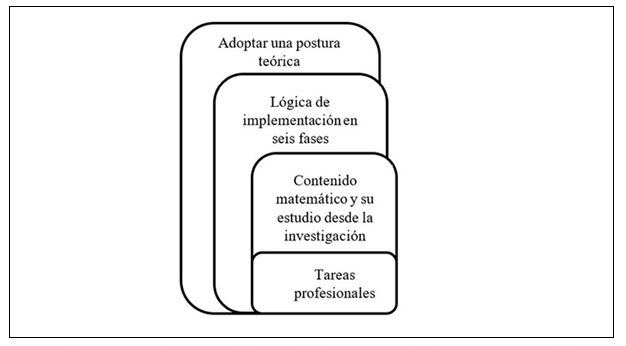
Para comenzar con la fase inicial, se plantea la primera tarea profesional con dos situaciones (Figura 4). La primera situación muestra la comparación entre binomios conjugados y binomio al cuadrado, haciendo hincapié en el error donde los alumnos dan por válida la distributiva de la potencia y dan por hecho la equivalencia en el procedimiento de dichos productos notables. La segunda situación plantea errores que normalmente los estudiantes cometen al momento de resolver un binomio al cuadrado, pero se utiliza un contexto aritmético y también se muestra su resolución acertada.

Figura 4:  Fuente: Tarea profesional 1 sobre error en el binomio al cuadrado 

La fase individual comienza con el planteo de preguntas a los docentes con la finalidad de dirigir la discusión sobre la situación analizada. Estas cuestiones tienen la intención de generar posibles conjeturas que expliquen el error del estudiante, así como también vincularlo con la enseñanza. Para la primera situación se pregunta:

• 1.En relación con la situación planteada, ¿cuál es el razonamiento que condujo al alumno a desarrollar los productos notables de esa manera?

• 2.¿El razonamiento expuesto por el alumno pudo ser resultado de alguna práctica específica por parte del docente en el aula?

• 3.¿Es posible que a través de un tratamiento aritmético pueda analizarse la estructura de los productos notables?

• 4.¿De qué modo se puede tratar el error expresado en las resoluciones?

• 5. Escribe un ejemplo que sea de apoyo en la compresión de ambos productos notables.

Respecto a la segunda situación, las preguntas que se le plantean al docente tienen la intención de contrastar las potencialidades del tratamiento aritmético para la comprensión del binomio al cuadrado, reconociendo también las desventajas de usar dicho tratamiento.

• 1. Como profesor de matemáticas, ¿cómo llevarías a cabo la introducción al tema de los productos notables utilizando la aritmética?

• 2. ¿Es pertinente un abordaje de los productos notables utilizando un contexto aritmético?

• 3. ¿Cuáles serían las ventajas y desventajas que puede enfrentar el alumno de acuerdo con los procedimientos planteados en la situación, considerando la estructura de estos?

• 4. ¿Qué preguntas plantearías a tus estudiantes tomando como referencia la situación planteada, de tal manera que esos cuestionamientos aporten a la compresión de los errores, al igual que a la resolución adecuada?

Luego, en la fase grupal, los futuros docentes expondrán las respuestas que articularon para discutir cuáles les parecen más acertadas y por qué. Es importante rescatar y destacar las opiniones sobre cómo utilizarían el contexto aritmético para el tratamiento del binomio al cuadrado. No se trata de categorizar las respuestas como incorrectas o correctas, sino de dialogar sobre las implicaciones que puede tener en el aula el modo de concebir la situación expuesta.

Posteriormente, en la fase teórica, se entrega a los docentes en formación una última hoja de trabajo donde se les propone realizar la lectura de un texto relativo a la investigación en Didáctica de la Matemática. La intención es confrontar sus respuestas intuitivas con los planteamientos que realiza ^{Socas (2007}), para lo que el profesorado en formación deberá contestar las siguientes preguntas en relación al texto:

• 1. ¿Cómo se interpreta al error?

• 2. ¿A qué se deben los errores?

• 3. ¿Es posible generar un aprendizaje a partir de los errores de los estudiantes? Explica.

• 4. ¿Qué elementos se deben considerar durante la enseñanza para el estudio y tratamiento de los errores?

En esta fase teórica se pretende conectar al menos dos ideas fundamentales: el error puede tener su origen en un aprendizaje que ya fue adquirido por el alumno, por lo que necesariamente no implica una falta de conocimiento, y el error puede tener un uso didáctico para la adquisición de conocimiento. Estos elementos son los que se consideran para llevar a cabo la fase de reajuste, que debe iniciarse con las impresiones de los futuros docentes respecto a la lectura realizada. A modo de mesa de discusión, los participantes expondrán sus respuestas y se motivará a que revisen sus producciones previas y propongan cambios. Deben pensar en un modo alternativo para abordar el binomio al cuadrado en el aula, considerando las dos situaciones planteadas y el texto analizado.

Tarea profesional 2. Análisis de representaciones y de la actuación docente

La segunda tarea profesional, en su fase inicial, plantea una situación que se corresponde con el análisis de un episodio de clase (Figura 5). Se pretende que a través de este episodio se promueva la reflexión sobre el uso de representaciones y explicaciones didácticas que se involucran en el desarrollo del tema.

Figura 5: Fuente: Episodio de clase sobre abordaje geométrico del tema de binomios conjugados 

La fase individual comienza con el planteo de preguntas que tienen la intención de generar posibles conjeturas sobre la manera en la que se utiliza la interpretación geométrica de los binomios conjugados. En específico, centrar que el uso de la representación geométrica por parte del docente tiene un carácter expositivo y que, por tanto, motiva un rol de espectador en el alumno.

• 1. ¿Cuáles son las ventajas y desventajas del desarrollo de la interpretación geométrica expuesta en el episodio?

• 2. ¿Qué errores se pueden generar al realizar un abordaje del tema como el anterior?, ¿por qué?

• 3. ¿De qué manera abordarías el tema de binomios conjugados utilizando la interpretación expuesta en el episodio? Explica.

• 4. ¿Existen elementos que favorecen la memorización o el aprendizaje significativo?, ¿por qué?

En la fase grupal, los futuros docentes expondrán las respuestas que articularon para discutir sus ideas e intentar llegar a consensos. Luego, en la fase teórica, se les entrega una última hoja de trabajo donde se le propone realizar una lectura. La intención es confrontar sus respuestas con el desarrollo de ^{Llinares (2004}), para lo que deberán contestar las siguientes preguntas relacionadas con el artículo:

• 1.¿Cómo se interpreta el significado de “ser profesor de matemáticas” en el documento?

• 2. ¿En qué consiste la práctica del profesor de matemáticas?

• 3. ¿Cómo se interpretan a los problemas y a los modos de representación del objeto matemático en la lectura?

• 4. ¿Qué elementos matemáticos y didácticos se consideran por el docente para llevar a cabo su práctica educativa?

Durante esta fase teórica se aborda el papel de las representaciones del objeto matemático y el papel del profesor en el trabajo matemático del estudiante respecto al uso de las representaciones. Durante la fase de reajuste se retoman estos elementos y se dialoga sobre lo que se evidencia en la lectura. Se focaliza en sus interpretaciones sobre la representación geométrica y su papel como agente de enseñanza, que puede ser vista desde la didáctica clásica como un artista que domina el arte de enseñar (^{Gascón, 1998}; ^{Rico y Sierra, 2000}; ^{Godino, 2010}) o desde la DM como un agente que gestiona el aprendizaje del aula. Se motiva a que revisen sus producciones y propongan cambios en sus respuestas, para luego enfocarse en la generación de estrategias que orienten el tratamiento de los binomios conjugados en el aula tomando a consideración los episodios analizados y la lectura realizada.

Finalmente, en ambas tareas profesionales, la fase de retroalimentación es guiada por el formador de profesores, quien alude a las aportaciones de los profesores de matemáticas y conecta con la teoría de las lecturas planteadas.

La propuesta hipotética desarrollada para el trabajo con profesores pretende centrar la atención en los elementos del conocimiento especializado del contenido y sobre el contenido matemático y los estudiantes. También pone a foco lo que el profesor debe saber en relación con el contenido matemático y su enseñanza, pues dependiendo de la naturaleza del objeto matemático a enseñar es su tratamiento en el aula.

Resulta imperante proporcionar áreas de oportunidad para desarrollar los conocimientos específicos sobre la enseñanza de las matemáticas en la formación de profesores, ya que además del tema que va a enseñar, debe saber a profundidad los procedimientos que favorecen el aprendizaje del alumno en la disciplina. A su vez, es preciso incorporar las investigaciones a la formación del profesorado con la finalidad de acortar la brecha entre los avances de la investigación en la educación y las aulas de clase, al mismo tiempo que se proporciona orientación fundamentada para la toma de decisiones sobre la enseñanza y el aprendizaje de las matemáticas.

Consideraciones finales

El diseño y el rol de tareas en la formación del profesor es una tendencia en las investigaciones en Didáctica de la Matemática (^{García-González, 2013}). Por ejemplo, ^{García (2019)} señala que cuando se piensa en el diseño de tareas este puede tener dos roles: el primero es estar subordinado al interés del investigador por indagar algún aspecto de la enseñanza y el aprendizaje matemático en los profesores; el segundo está orientado a considerar a las tareas como materiales y recursos para el aula. En la propuesta presentada aquí, el papel del diseño de tareas para la formación del profesorado es un punto de inflexión para el desarrollo de sus conocimientos.

Considerar al MKT como referente teórico en este trabajo, no es que se pretenda como el único camino, pues es posible considerar otro. No es el objetivo proponer un diseño a partir de un marco teórico específico, como los ejemplos expuestos en ^{García (2019}) y en ^{Hinojos, Romero y Farfán (2020}) en el marco de la socioepistemología. En este sentido, el diseño de tareas no es rígido y la intención de las tareas aquí planteadas es la vinculación de los resultados de las investigaciones en la práctica docente a través de la formación del profesor de matemáticas.

Este artículo pretende evidenciar una forma de relacionar la DM en las aulas, con los profesores, a fin de proporcionar esas herramientas teórico-metodológicas y avanzar en el desarrollo del conocimiento matemático y didáctico. Independientemente de la postura teórico-metodológica de la disciplina, el ciclo que vincula los resultados de las investigaciones con los procesos formativos docentes y realidad del aula se presenta en la siguiente Figura 6:

Figura 6: Fuente: Ciclo de vinculación de la investigación y la docencia 

En este marco, el tipo de tareas profesionales que precisan plantearse durante la formación de profesores deben ser situaciones vinculadas a su práctica o futura práctica educativa y guiadas teóricamente por los resultados de las investigaciones para promover el desarrollo de sus conocimientos y competencias. Tal como expresa ^{Llinares (2012}): “la forma en que los profesores puedan llegar a usar su conocimiento del contenido matemático y el conocimiento de didáctica de la matemática condicionan su propia práctica” (p. 113). La propuesta planteada se corresponde con el hecho de que las tareas que los profesores realizan en los programas de formación desempeñan un papel relevante en el aprendizaje del conocimiento matemático necesario para enseñar las matemáticas en situaciones prácticas (^{Llinares, 2012}).

Aún quedan cuestiones a considerar para consolidar esta propuesta de diseño de tareas profesionales. Una de ellas es definir el papel del formador de profesores de matemáticas que implementaría estas acciones en los cursos de formación: ¿quiénes son los que fungen como formadores de estos profesores en México? Este es un campo poco explorado (^{Hernández, Sosa, y López, 2013}), aunque, de acuerdo con ^{Llinares (2014}), el papel del formador de profesores es crucial para exteriorizar el acervo de aportaciones entre la investigación (en Didáctica de la Matemática) y la práctica para hacerlas parte de la actividad profesional del docente. De este formador depende qué y cómo aprenden los profesores de matemáticas en formación y en servicio, y el modo en el que se retroalimentan las decisiones de la práctica de enseñanza a partir del conocimiento generado por la investigación.