APRENDIZAJE CONSTRUCTIVO, AUTORREGULADO, SITUADO Y COLABORATIVO: UN ACERCAMIENTO A LA ADQUISICIÓN DE LA COMPETENCIA ADAPTATIVA (MATEMÁTICA)

Constructive, self-regulatory, situated and collaborative learning: an approach to the acquisition of the adaptative competency in mathematics

ERIK DE CORTE^*

Resumen. Actualmente, en una sociedad de aprendizaje, la educación debe centrarse en fomentar la Competencia Adaptativa (AC por sus siglas en inglés: Adaptative Competence) que se define como la habilidad de aplicar de manera flexible conocimientos y destrezas en diferentes contextos. En este artículo se discuten tres preguntas: ¿Qué deben aprender los estudiantes a fin de adquirir la AC en un campo particular? ¿Cuáles son las características que se requieren en un proceso de aprendizaje productivo para obtener la competencia adaptativa? ¿Cómo se puede estimular y prolongar este aprendizaje a través de la instrucción? Este artículo presenta un estudio ilustrativo enfocado en el diseño de un ambiente de aprendizaje para mejorar la competencia de resolución de problemas en estudiantes de educación primaria. Las acotaciones finales indican los retos de la implementación de ambientes de aprendizaje innovadores.

Palabras clave: aprendizaje constructivo, autorregulación, Competencia Adaptativa, matemáticas, Educación Primaria

Abstract. Currently, in a learning society, education should focus on promoting Adaptive Competition (AC) which is defined as the ability to flexibly apply knowledge and skills in different contexts. This article discusses three questions: What should students learn to acquire the AC in a particular field? What are the features that are required in a productive learning process for AC? How can stimulate and extend this learning through instruction? This paper presents an illustrative study focused on the design of a learning environment to improve the competence of problem solving in primary school students. The final dimensions indicate the challenges of implementing innovative learning environments.

Keywords: constructive learning, self regulation, adaptative competency, mathematics, primary

Recibido el 19 de junio de 2015

Revisado el 14 de setiembre de 2015

Aceptado el 1 de octubre de 2015

 

En un reporte de la Mesa Redonda de Industriales Europeos (1995) se define a la sociedad de aprendizaje actual de acuerdo con las siguientes características:

El aprendizaje es aceptado como un actividad continua a lo largo de la vida; los aprendices asumen la responsabilidad de su propio progreso; la evaluación es diseñada para confirmar el progreso antes que para sancionar el fracaso; se reconoce la competencia personal y los valores compartidos, y el espíritu de equipo, al igual que la búsqueda de conocimiento; el aprendizaje es una sociedad entre estudiantes, profesores, padres, empleados y una comunidad que trabajan juntos. (15)

De acuerdo con esta consideración, la educación, en todos los niveles, debe centrarse aún más en desarrollar y propiciar en los estudiantes la Competencia la AC, esto es, la habilidad de aplicar de manera significativa, flexible y creativa el conocimiento y las destrezas aprendidas en una variedad de contextos. El acercamiento descrito en este artículo se opone a aquellos utilizados para desarrollar una experticia rutinaria, como la habilidad para completar las típicas tareas escolares de manera rápida y exacta, pero sin entender el proceso que se requería para cumplir la tarea.

La discusión inicial se centrará e ilustrará en aquello que los estudiantes deben aprender a fin de adquirir la competencia de adaptación en un área en particular. Luego se abordará la pregunta clave: ¿Cuáles son las características que se requieren en un proceso de aprendizaje productivo y significativo para obtener la competencia adaptativa? La discusión se centrará en cuatro características importantes: el aprendizaje constructivo, autorregulado, situado y colaborativo (CSSC por siglas en inglés: Constructive, Self-regulated, Situated, Collaborative).El acercamiento integrará las metáforas de aprendizaje relativas a la adquisición y participación o los aspectos individuales y sociales del aprendizaje.

Desde la perspectiva de enseñanza, la pregunta que se establece es: ¿Cómo se puede estimular y prolongar los aprendizajes CSSC a través de la instrucción? Se presentará un estudio que se enfoca en el diseño, implementación y evaluación de un ambiente de aprendizaje para mejorar la competencia de resolución de problemas en estudiantes de grados avanzados de educación primaria. El artículo concluirá con comentarios finales que abordan el punto clave de una implementación efectiva y sustentable de ambientes innovadores de aprendizaje en la práctica diaria de aula.

¿QUÉ DEBEN APRENDER LOS ESTUDIANTES?

Varios expertos en el área de educación concuerdan en que la meta más importante de la instrucción y el aprendizaje en los campos académicos consiste en la adquisición de un alto grado de “experticia adaptativa” (Hatano e Inagaki, 1986; Hatano y Oura, 2003; Bransford et al., 2006) o lo que se conoce como “competencia adaptativa” en oposición a “experticia rutinaria”. A pesar de distinguir diferentes niveles de experticia, (Hatano y Oura, 2003), este término se asocia con niveles excepcionales de rendimiento. Debido a esta connotación, será usado el término “competencia”, ya que no se puede esperar que la mayoría de estudiantes alcancen un rendimiento excepcional en las materias del currículo escolar. Construir la competencia de adaptación en un área, requiere la adquisición de varios componentes cognitivos, afectivos y motivacionales:

1. Una base de conocimiento específico bien organizado y de acceso flexible en un determinado campo que involucre hechos, símbolos, conceptos y reglas que constituyen el contenido de un tema en un área.

2. Métodos heurísticos, esto es, estrategias para análisis y transformación de problemas (por ejemplo, descomposición de un problema en sub-metas, realización de representaciones gráficas de un problema) lo que no garantiza pero aumenta considerablemente la probabilidad de encontrar la solución correcta por medio de inducir un acercamiento sistemático a la tarea.

3. Meta-conocimiento que implica el conocimiento acerca del propio funcionamiento cognitivo o conocimiento metacognitivo (por ejemplo, conocimiento de que el potencial cognitivo puede desarrollarse a través del aprendizaje y esfuerzo) y conocimiento sobre la motivación y las emociones que pueden usarse activamente para mejorar el aprendizaje (por ejemplo, toma de conciencia sobre los propios temores en el fracaso de las matemáticas).

4. Destrezas autorreguladoras para que uno mismo pueda regular actividades y procesos cognitivos (“destrezas metacognitivas” o “auto-regulación cognitiva” (por ejemplo, planificación y monitoreo de procesos de solución de problemas) y destrezas para regular actividades y procesos emocionales y volitivos (“auto-regulación motivacional”, por ejemplo, mantener la atención y la motivación para resolver un problema dado).

5. Afecto positivo, esto es, emociones y actitudes positivas hacia campos académicos y hacia el aprendizaje, así como también una creencia de auto-eficacia positiva (De Corte, 2010).

Priorizar la competencia de adaptación no significa que el conocimiento rutinario deje de tener importancia; es obvio pensar que el dominio de ciertas destrezas rutinarias (aritmética básica, deletreo, destrezas técnicas) es importante para funcionar en todo tipo de situación. Si ciertos aspectos de solución de problemas complejos pueden realizarse más o menos mecánicamente, dicha automatización permite que el estudiante centre su atención en actividades de mayor grado cognitivo necesarias para alcanzar la solución. Sin embargo, la competencia de adaptación es importante porque va más allá de eso, “implica el deseo y la habilidad de cambiar competencias centrales y expandir continuamente el grado y profundidad de la habilidad propia” (Bransford et al., 2006: 223). Por lo tanto, es fundamental que uno transfiera su propio conocimiento y destrezas hacia las nuevas tareas y contextos de aprendizajes (De Corte, 2007; Hatano y Oura, 2003) y hacia un aprendizaje a lo largo de la vida.

Como se documentará, la literatura disponible muestra la importancia de la competencia adaptativa de dos maneras. Primero, una abundante evidencia muestra la falta de uno o más componentes en los estudiantes novatos o de bajo desempeño en un tema determinado. (Garner, 1987; Schoenfeld, 1985). Segundo, un buen número de investigaciones demuestra que la adquisición del dominio de esos componentes a través de la instrucción mejora el acercamiento de los estudiantes al problema, lo que resulta en mejores resultados en el rendimiento (Brown y Palincsar, 1989; De Corte, Verschaffel y Masui, 2004). Una discusión ampliada de estos cinco componentes desde estas dos perspectivas está fuera del alcance de este artículo. Por lo tanto, documentaré breve y selectivamente la importancia de los siguientes componentes: el conocimiento específico en un campo, destrezas heurísticas y auto-regulación cognitiva, y las creencias sobre campos académicos.

Con respecto al conocimiento de un dominio específico, la investigación ha demostrado que muchos estudiantes tienen un conocimiento superficial y a menudo deficiente de conocimientos básicos en varios campos y, más aún, tienen conceptos erróneos. Por ejemplo, muchos estudiantes, al término de su educación primaria, piensan que la multiplicación resulta ser un número mayor mientras la división es lo contrario. Se han observado varios conceptos erróneos en el campo de la física, por ejemplo, que los objetos pesados caen más rápidamente que los livianos o que se necesita una fuerza continua para un movimiento continuo (De Corte, Greer, y Verschaffel, 1996).

En un estudio clásico entre expertos y novatos realizado por Michelene Chi, Paul Feltovich y Robert Glaser (1981), se pidió a estudiantes de un doctorado en física (expertos) y estudiantes de pre-grado (novatos) que habían terminado un curso de mecánica, que ordenaran 24 problemas de física basándose en similitudes de solución. Los resultados mostraron que la clasificación hecha por los expertos se basaba en principios físicos subyacentes o en leyes necesarias para solucionar el problema (una representación científica del problema); los novatos usaron para su clasificación características superficiales de los problemas tales como el equipo involucrado en la tarea, aspectos superficiales de un diagrama o términos en la declaración del problema (una representación ingenua del problema). Estas diferentes representaciones de los problemas reflejan diferencias en el contenido y en la organización del conocimiento específico de un campo base entre expertos y novatos. Junto a otros estudios en diferentes áreas, éste muestra el rol importante que juega el conocimiento específico en un área en el aprendizaje y resolución de problemas, especialmente en relación con la construcción de un punto de partida apropiado para la tarea de aprendizaje o un problema (Chi, Glaser y Farr, 1988; Ericsson, 2003; Schraw, 2006).

La falta de dominio y uso de métodos heurísticos y de destrezas cognitivas autorreguladoras también se ha demostrado claramente, por ejemplo, en la resolución de problemas matemáticos, en la comprensión lectora y en la escritura de textos. Los métodos heurísticos son estrategias para el análisis de problemas que tienen como objetivo la transformación de una situación problemática en una tarea de rutina, para la cual quien soluciona los problemas tiene el conocimiento y las destrezas disponibles para hacerlo (De Corte, 2010). Se puede considerar ejemplos adicionales como el análisis minucioso de un problema, la ubicación de problemas análogos, la visualización del problema, el trabajo desde la solución intentada y el abandono provisional de un requisito para la solución.

Las estrategias autorreguladoras constituyen una estructura de control ejecutivo que organiza, guía y monitorea los procesos del pensamiento y del aprendizaje. Ejemplos de esta naturaleza pueden ser la planificación de un proceso de solución, el monitero un proceso en construcción, la evaluación y depuración de una solución, la reflexión sobre la solución final. Los aprendices y quienes solucionan con éxito los problemas pueden realizar simultáneamente dos funciones, a saber: la ejecución y elaboración de la solución, y la regulación de actividades relacionadas con la tarea, lo que incluye orientación, planificación, monitoreo, evaluación y reflexión.

La carencia de destrezas heurísticas y autorreguladoras en novatos ha sido demostrada fehacientemente por Alan Schoenfeld (1992) quien filmó, durante sesiones de 20 minutos, el trabajo en parejas de estudiantes de colegio y de universidad que realizaban un problema matemático no familiar y luego contrastó sus procesos resolutivos con aquellos de los expertos. Los procesos fueron separados en episodios representando diferentes actividades, como la lectura del problema, el análisis, la exploración, la planificación, la implementación y la verificación. Cerca del 60% de los intentos resolutivos de los novatos carecían totalmente de actividades heurísticas (como el análisis del problema) y autorreguladoras (como el monitoreo del proceso) que son características del planteamiento de los expertos. Las estrategias típicamente registradas se las puede resumir en: lectura del problema, decisión rápida sobre la solución y su ejecución sin consideración de otras alternativas, aunque no haya progreso alguno. En un estudio anterior Schoenfeld (1985) descubrió que, al enseñar destrezas heurísticas y autorreguladoras, se mejoraba también la habilidad resolutiva de problemas.

Con respecto a la lectura comprensiva, Ruth Garner (1987) ha documentado que el dominio y uso de buenas destrezas reguladoras, tales como la re-inspección del texto, diferencian al buen lector del mal lector. Otros investigadores han encontrado que la enseñanza de estrategias para mejorar la lectura comprensiva y la escritura tiene un efecto positivo en la comprensión lectora del estudiante (Brown, Pressley, Van Meter, y Schuder, 1996; De Corte, Verschaffel y Van De Ven, 2001), y en la destreza escrita respectivamente (Scardamalia, Bereiter y Steinbach, 1984).

En resumen, la evidencia empírica disponible sugiere que los estudiantes más exitosos dominan de manera más efectiva y sofisticada las destrezas heurísticas y autorreguladoras, y se demuestra también que, dichas destrezas, pueden ser aprendidas tempranamente, digamos que en el primer nivel de educación primaria, si se provee a los estudiantes con una instrucción apropiada. Además, las destrezas autorreguladoras posibilitan la habilidad de transferir nuestro conocimiento y destrezas hacia nuevos problemas y tareas. Ann Brown y Joe Campione (1994) observaron un adelanto en los resultados de lectura comprensiva con material fuera del campo de la biología visto por los estudiantes en la clase (De Corte, 2003).

La importancia del afecto positivo en el aprendizaje, especialmente en lo referente a creencias sobre la auto-eficacia y creencias epistemológicas, tuvo su valor y énfasis en la década pasada (Bendixen y Feucht, 2010). Se ha demostrado que las creencias epistemológicas, es decir, las creencias sobre el conocimiento y aprendizaje, afectan el grado de involucramiento en el aprendizaje, en la persistencia en las tareas difíciles, en la comprensión del material escrito, en el acercamiento y solución exitosa a problemas complejos en campos débilmente estructurados (Schommer, 1994b).

Sin embargo, la investigación en las dos últimas décadas revela que, en muchos temas y en diferentes campos, los estudiantes sostienen creencias que son ingenuas, incorrectas o ambas, y que estas creencias pueden tener un efecto negativo e inhibitorio en las actividades y acercamientos de aprendizaje. Con respecto a las matemáticas, muchos estudiantes piensan que es un cuerpo establecido de conocimiento establecidos y no un conocimiento construido por el estudiante. Los siguientes puntos de vista son comunes entre los alumnos con relación a su concepción: las matemáticas se asocian con certezas y con la capacidad de dar una respuesta rápida; hacer matemáticas corresponde a seguir reglas descritas por el profesor; una respuesta a una pregunta o problema matemático se convierte en verdadera cuando el profesor la aprueba (De Corte, Verschaffel y Op ‘t Eynde, 2000). Una ilustración pertinente de estos defectos en las creencias de los estudiantes proviene de un estudio de Susan Picker y John Berry (2000) quienes pidieron a 476 estudiantes de 12 y 13 años de cinco países (Finlandia, Rumania, Suecia, Reino Unido y Estados Unidos) hacer un dibujo de un matemático y comentar sobre éste por escrito. Se obtuvieron dos categorías diferentes de dibujos: algunos estudiantes representaron a un matemático que claramente no era un profesor, pero otros dibujaron la imagen de un matemático como profesor. Un tema importante y común entre los dibujos y comentarios de los sujetos de investigación de los cinco países fue la concepción de las matemáticas como imposición: la esencia de muchos dibujos de los estudiantes era, en realidad, aquella de pequeños niños sin poder de decisión confrontando a un matemático representado como autoritario y amenazador. Como es verosímil asumir que los dibujos de los estudiantes reflejan sus creencias acerca de las matemáticas, es obvio pensar que ellos no perciben este campo como interesante, atractivo y motivador.

Con respecto a la lectura comprensiva, Marlene Schommer (1994a) reportó las concepciones ingenuas que juegan un papel importante en varios aspectos de la lectura: aprender a leer significa memorizar las palabras; leer para aprender significa memorizar los hechos, y leer para aprender debe ser un proceso rápido que revele un conocimiento absoluto y certero. Con respecto a la historia, Samuel Wineburg (1991) observa creencias absurdas: los reportes históricos son meras colecciones de “hechos”, y aprender historia es aceptar y absorber pasivamente la información basada en hechos. Nancy Songer y Marcia Linn (1991) demostraron que muchos estudiantes creen que el conocimiento en la ciencia resulta en pequeñas porciones de conocimiento aislado y estático.

CARACTERÍSTICAS DE PROCESOS PRODUCTIVOS DE APRENDIZAJE PARA LA ADQUISICIÓN DE LA COMPETENCIA DE ADAPTACIÓN

A fin de conseguir la competencia de adaptación y superar las deficiencias discutidas anteriormente, y para tomar en cuenta la importancia de factores contextuales y sociales que afectan el aprendizaje, el aprendizaje escolar contemporáneo debe encarnar más un concepto que puede definirse como un proceso activo, constructivo, acumulativo, autorregulado, orientado a una meta, situado, colaborativo e individualizado de construcción de significados, conocimientos y destrezas. Estas características de un aprendizaje productivo y significativo están sustentadas por un número importante de investigaciones (De Corte, 2010; Kirby y Lawson, 2012; National Research Council, 2000; 2005). Debido a la imposibilidad de revisar todos los estudios, la siguiente discusión se centra en cuatro características claves anunciadas anteriormente: aprendizaje constructivo, autorregulado, situado y colaborativo (CSSC) construido en el conocimiento previo del estudiante y tomando en cuenta las diferencias individuales. Las tres viñetas en el anexo A presentan ejemplos concretos.

EL APRENDIZAJE ES CONSTRUCTIVO

La perspectiva constructivista del aprendizaje ha tomado cuerpo entre los psicólogos educativos (Simons, van der Linden y Duffy, 2000). Los aprendices son vistos no como receptores pasivos de información sino como constructores activos de conocimientos y destrezas a través de una reorganización de sus estructuras mentales adquiridas previamente. Actualmente hay mucha evidencia en el sentido de que el aprendizaje es, de alguna manera, siempre constructivo, así sea en ambientes donde prevalece la instrucción directa. Esto se observa en la investigación que demuestra la ocurrencia de conceptos erróneos mencionados anteriormente (tales como que la multiplicación agranda) y a destrezas procesales defectuosas (como se ilustra en la viñeta 1) entre los estudiantes en clases tradicionales de matemáticas. Como sugiere Giyoo Hatano, “es bastante improbable que los estudiantes las hayan adquirido a través de la enseñanza” (1996: 201).

Lo que es esencial en la perspectiva constructivista es el involucramiento significativo y el esfuerzo que ponen los estudiantes en el proceso de adquisición de conocimiento y destrezas en interacción con el ambiente. Esto se demuestra por el procedimiento raro y difícil, pero exacto, del niño vendedor ambulante de Brasil en la viñeta 2. En trabajos previos (De Corte y Verschaffel, 1987) se encontró evidencia que apoyaba esta visión constructiva del aprendizaje de los niños, incluso en el simple campo de resolver una suma y resta sencillas. En verdad, estudiantes de primer grado usaban una gran variedad de estrategias resolutivas, muchas de ellas no enseñadas en la escuela sino construidas por ellos mismos. La gran cantidad de evidencia a favor de la naturaleza constructivista del aprendizaje se alinea con estudios previos realizados por reconocidas autoridades en el campo como Jean Piaget (1955) y Jerome Bruner (1961).

EL APRENDIZAJE ES AUTORREGULADO

El aprendizaje constructivo es también autorregulado. Como sugiere Barry Zimmerman, “los individuos son metacognitiva, motivacional y conductualmente activos participantes en sus propios procesos de aprendizaje” (1994: 3). Si los estudiantes pretenden convertirse en aprendices a través de la vida, ellos deben ser capaces de manejar y monitorear sus procesos de construcción de conocimiento y adquisición de destrezas. Esta característica de aprendizaje se ilustra en la viñeta 2 (anexo A) en el raro proceso de cálculo del vendedor de la calle de Brasil.

A pesar de que la investigación en el campo de la autorregulación en la educación comenzó solamente hace 25 años, una gran cantidad de trabajos empíricos y teóricos han arrojado importantes consideraciones (Boekaerts, Pintrich, y Zeidner, 2000; Zimmerman y Schunk, 2011). Primero, se han identificado las principales características de estudiantes autorregulados. Estos estudiantes manejan bien el tiempo de dedicación al estudio, se fijan metas inmediatas más altas que son monitoreadas por ellos con más frecuencia y precisión, se imponen estándares más altos de satisfacción, y son más autoeficaces y persistentes a pesar de todos los obstáculos. Segundo, la autorregulación se correlaciona fuertemente con logros académicos en las diferentes áreas de estudio (Zimmerman y Risemberg, 1997). Debido a que la investigación muestra también que los estudiantes no adquieren estrategias sofisticadas de autorregulación espontáneamente, la autorregulación no es únicamente un elemento del aprendizaje productivo, sino que, como componente de la competencia de adaptación, constituye en sí mismo una meta para el proceso de aprendizaje a largo plazo que debe ser alentado desde temprana edad (De Corte, Mason, Depaepe y Verschaffel, 2011).

EL APRENDIZAJE ES SITUADO O CONTEXTUALIZADO

1.La comunidad de investigadores educativos sostiene fuertemente la idea de que el aprendizaje constructivo y autorregulado debe ocurrir en un contexto, es decir, en relación al ambiente social, contextual y cultural donde estos procesos están inmersos y que influyen en su desarrollo (ver Kirschner y Whitson, 1997; National Research Council, 2000). La perspectiva del aprendizaje situado enfatiza que éste se realiza esencialmente con la interacción y, especialmente, a través de la participación en actividades y contextos sociales y culturales. Esto se ilustra también en la viñeta 2 por el proceso de cálculo inventado por el vendedor ambulante en Brasil, en su contexto real de hacer su negocio. En matemáticas, la perspectiva situada ha estimulado el cambio hacia una educación matemática más auténtica y realista (De Corte et al., 1996).

EL APRENDIZAJE ES COLABORATIVO

La naturaleza colaborativa del aprendizaje está estrechamente vinculada con la perspectiva situada que enfatiza su carácter social. El aprendizaje efectivo es una actividad distribuida y no simplemente aislada. El esfuerzo de aprendizaje está distribuido entre el estudiante en sí, los compañeros del ambiente de aprendizaje, y los recursos, tecnología y herramientas disponibles (Salomon, 1993). Por ejemplo, la interacción social es esencial para el aprendizaje de las matemáticas, como sucede con la construcción individual de conocimiento a través de la interacción, negociación y cooperación (Wood, Cobb y Yackel, 1991). La viñeta 3 ofrece una ilustración con una actividad en la forma del jigsaw método.

La literatura provee evidencia importante que apoya los efectos positivos que tiene un aprendizaje colaborativo en el logro académico (Lehtinen, 2003; Salomon, 1993; Slavin, 2010). Se sugiere que un cambio hacia una interacción social en el aula representaría un alejamiento valioso del énfasis tradicional sobre el aprendizaje individual; el aprendizaje puede ser más productivo a través de la implementación de la colaboración entre estudiantes en actividades como el intercambio de ideas, la comparación de estrategias de solución y la discusión de argumentos. Es importante considerar que dichas actividades deben conducir a la reflexión para así motivar la autorregulación cognitiva del aprendizaje. Sin embargo, se debe evitar ir lejos en la dirección contraria, ya que aprender a colaborar e interactuar no excluye el desarrollo individual del nuevo conocimiento.

RESPUESTAS A CRÍTICAS SOBRE LOS ACERCAMIENTOS CONSTRUCTIVISTAS

La comprensión del aprendizaje, según lo descrito anteriormente, es una amplia representación de la perspectiva constructivista donde se combinan e integran la adquisición y la participación (Sfard, 1998) o los aspectos individuales y sociales del aprendizaje (Salomon y Perkins, 1998). A pesar de que la literatura disponible ofrece el apoyo para el aprendizaje cognitivo, autorregulado, situado y colaborativo (Bransford et al., 2006; National Research Council, 2000; 2005), la perspectiva constructivista también ha merecido críticas. Paul Kirschner, John Sweller y Richard Clark (2006) argumentan que los acercamientos basados en el constructivismo confían de manera excesiva en el aprendizaje por descubrimiento y ofrecen una guía mínima al estudiante ignorando, como resultado de esta acción, la estructura de la arquitectura cognitiva humana y dando como resultado una sobrecarga cognitiva de la memoria de trabajo. Estos autores apuntan hacia el retorno a la instrucción directa.

Si bien es cierto que las críticas son correctas en el sentido de que únicamente el descubrir no apunta hacia una mejor ganancia en el aprendizaje, como lo evidencia Mayer (2004) en su revisión de la literatura de los últimos 50 años, el aprendizaje constructivista no puede ser equiparado con el aprendizaje por descubrimiento. El concepto de aprendizaje como un proceso activo, constructivo, autorregulado no significa que la construcción de conocimientos y destrezas de los estudiantes no puedan y no deban ser guiados y mediados a través de un modelaje, entrenamiento, retroalimentación, ejemplos y andamiaje apropiados por parte de profesores, pares, y medios comunicativos de educación. Mayer concluye, por reportes de estudios, que el descubrimiento guiado conduce a mejores logros de aprendizaje que la instrucción directa. Un ambiente de aprendizaje fuerte e innovador se caracteriza por tener un balance efectivo entre el descubrimiento y la exploración personal, y una instrucción y guía sistemática siendo sensibles a las diferencias de habilidades, necesidades y motivación de los estudiantes. Un reciente meta-análisis de investigación relevante, confirma la conclusión de Mayer: la enseñanza directa es mejor que el descubrimiento no asistido, pero el aprendizaje por descubrimiento guiado, motivado o asistido es superior a la enseñanza directa o explicita (Alfieri, Brooks, Aldrich y Tenenbaum, 2011). Sin embargo, es importante notar que el balance entre la regulación externa por parte del profesor y la autorregulación por parte del estudiante variará durante el camino de aprendizaje de los estudiantes; según aumenta la competencia, la autorregulación puede crecer y el apoyo de la instrucción explicita puede disminuir. Conocedores de estas conclusiones, el diseño de ambientes de aprendizaje prevendrá una sobrecarga cognitiva y, al mismo tiempo, inducirá a una carga cognitiva pertinente que facilitará un aprendizaje efectivo (Schmidt, Loyens, van Gog y Paas, 2007).

DISEÑO DE AMBIENTES DE APRENDIZAJE QUE ESTIMULAN LOS PROCESOS DE APRENDIZAJE CSSC

A partir de la perspectiva de aprendizaje CSSC, el mayor reto desde la perspectiva de la enseñanza es saber cómo esos procesos de aprendizaje pueden ser estimulados y mantenidos a través de la intervención instructiva. El estudio, objeto de este artículo, se centra en el diseño, implementación y evaluación de un ambiente de aprendizaje que busca fortalecer los procesos de aprendizaje cognitivos, autorregulados, situados y colaborativos para la competencia de adaptación en la solución de problemas matemáticos entre estudiantes de un nivel avanzado de educación primaria (para un reporte más detallado, ver Verschaffel et al., 1999). El objetivo del estudio fue investigar si los estudiantes inmersos en este ambiente de aprendizaje tenían un mejor desarrollo de su competencia resolutiva de problemas, y también creencias más realistas y positivas con respecto a las matemáticas.

EL AMBIENTE DE APRENDIZAJE EXPERIMENTAL

El ambiente de aprendizaje en las aulas experimentales sufrió un cambio fundamental con respecto a los siguientes componentes: el contenido de la enseñanza-aprendizaje, la naturaleza de los problemas, las técnicas de instrucción, y la cultura de aula. Primero, se enseñó a los estudiantes una estrategia autorreguladora de cinco etapas para resolver problemas de aplicación matemática y un conjunto de ocho estrategias heurísticas que son especialmente útiles durante las dos primeras etapas del proceso (ver anexo B). La adquisición de esta estrategia para resolver problemas significó: 1) crear conciencia de las diferentes fases de un proceso competente para resolver problemas; 2) ser capaz de monitorear y evaluar las propias acciones durante las diferentes fases (entrenamiento autorregulado), y 3) incrementar el dominio de las ocho estrategias heurísticas (entrenamiento en estrategias heurísticas).

Segundo, se utilizó un conjunto de problemas reales, complejos y abiertos. Los problemas diferían sustancialmente de los problemas de los libros de texto tradicionales y se los presentó en diferentes formatos: un texto, un artículo de periódico, un folleto, una tira cómica, una tabla o una combinación de algunos de estos formatos. El ejemplo del anexo C ilustra el tipo de tareas usadas en el ambiente de aprendizaje.

Tercero, se creó una comunidad de aprendizaje a través de la aplicación de técnicas interactivas de instrucción, en particular, trabajo en grupos pequeños y discusión con toda la clase. El modelo de instrucción básica para cada lección consistió en la siguiente secuencia para las actividades de clase: 1) una introducción breve para toda la clase; 2) dos tareas grupales para ser resueltas en grupos heterogéneos de tres o cuatro alumnos seguidas cada una de ellas de una discusión con toda la clase, y 3) una tarea individual con la subsecuente discusión con toda la clase. Durante todas las lecciones, el papel del profesor fue el estímulo y la creación del andamiaje para involucrar a los estudiantes, y luego reflexionar sobre las actividades cognitivas y de autorregulación incluidos en la estrategia de cinco etapas para solucionar problemas. El apoyo en la instrucción fue gradualmente desapareciendo según los alumnos iban siendo más competentes y autorregulados en sus actividades de resolución de problemas.

Cuarto, se creó una cultura de clase innovadora al establecer normas nuevas sobre al aprendizaje y la enseñanza de resolución de problemas (Yackel y Cobb, 1996) apuntando a promover creencias positivas hacia las matemáticas. Los aspectos típicos de esta cultura de aula incluían: 1) la motivación para que los alumnos articularan y reflexionaran sobre sus estrategias de resolución y creencias acerca de la resolución de problemas; 2) la discusión sobre lo que es un buen problema, una buena respuesta y un buen procedimiento de resolución (por ejemplo, con frecuencia existen diferentes formas de solucionar un problema; para algunos problemas una estimación aproximada es mejor respuesta que un número exacto), y 3) la reconsideración del papel del profesor y de los estudiantes en una clase de matemáticas (por ejemplo, la clase, como un todo, decidirá cuál de las soluciones generadas es la óptima luego de analizar los pros y los contras de las diferentes alternativas).

El ambiente de aprendizaje se refinó en forma conjunta con los profesores de las aulas experimentales y sus directores. El modelo de apoyo a los profesores enfatizaba la creación de un contexto social en el que profesores e investigadores aprendieran uno del otro a través de discusiones y reflexiones continuas sobre los principios básicos del ambiente de aprendizaje, los materiales de aprendizaje desarrollados y las prácticas de los profesores durante las lecciones. El resultado fue un conjunto de diez directrices generales para los profesores donde se establecieron acciones específicas que ellos deben tomar y cómo se pueden involucrar con los estudiantes antes, durante y después de tareas individuales y grupales a fin de fortalecer el poder del ambiente de aprendizaje (ver anexo D). En la guía del profesor que se usó en el proyecto, cada directriz venía acompañada de una explicación sobre su propósito y se facilitaron ejemplos de implementación.

La intervención consistió en veinte lecciones, que fueron enseñadas en las aulas experimentales por los profesores regulares durante un período de cuatro meses en las horas escolares regularmente destinadas para matemáticas. Durante el mismo tiempo, los alumnos de las aulas del grupo control continuaron desarrollando el currículo de matemáticas regular que contenía un número considerable de lecciones sobre resolución de problemas, aunque con poca o ninguna atención hacia la enseñanza sistemática de destrezas heurísticas y de autorregulación.

DISEÑO DEL ESTUDIO

Participaron en el estudio cuatro aulas experimentales de quinto grado (n = 27, 19, 21, 19) y siete aulas de control comparables (n = 29, 22, 19, 21, 20, 17, 18). Todas estas aulas se encontraban en escuelas primarias de una región urbana de Bélgica e incluían estudiantes de los dos géneros y de diferentes clases socio-económicas. Todos los profesores eran calificados y certificados por un instituto de formación de profesores para educación básica y tenían por lo menos cinco años de experiencia

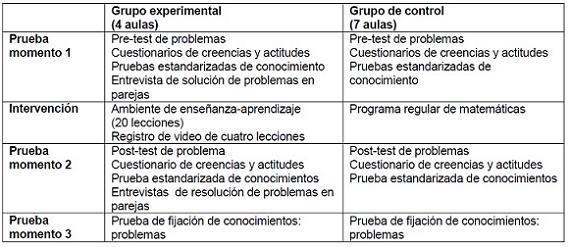
Los efectos del ambiente de aprendizaje fueron evaluados mediante el uso de un pre-test, un post-test y un test de retención con un grupo experimental y un grupo de control comparable aplicando una gran variedad de técnicas de recolección y análisis dedatos (ver anexo E). Las pruebas paralelas de problemas usadas como pre-test, post-test, y test de retención contenían diez tareas no rutinarias que les llevaba por su cuenta a aplicar las destrezas heurísticas y autorreguladoras enseñadas durante la intervención. El siguiente es un ejemplo tomado del examen:

Lies tiene dos casas de muñecas. El piso cuadrado de la casa pequeña tiene un lado de 40 cms. y tiene 16 azulejos. El piso cuadrado de la casa grande tiene un lado que es exactamente el doble del lado de la casa pequeña. ¿Cuántos azulejos se necesitan para el piso de la casa grande si se usan los mismos azulejos?

La respuesta de cada tarea fue registrada como correcta, incorrecta, error técnico de cálculo o sin respuesta.

El cuestionario diseñado consistió en 21 afirmaciones tipo escala de Likert y apuntaban a evaluar las creencias y actitudes de los estudiantes sobre la enseñanza y el aprendizaje de la resolución de problemas matemáticos. Se distinguieron dos sub-escalas basadas en un análisis factorial: una primera con afirmaciones que trataban sobre “el gusto y la persistencia en resolver problemas (ppor ejemplo, me gusta resolver problemas; los problemas difíciles son mis favoritos, etc.) y una segunda sub-escala con catorce afirmaciones que reflejaban un punto de vista orientado al proceso en la resolución de problemas (por ejemplo, en los problemas de matemáticas hay diversas formas para llegar a encontrar una solución correcta; escuchar las explicaciones de soluciones y caminos alternos de los alumnos es una pérdida de tiempo, etc.). En cada afirmación los estudiantes tenían que responder indicando si ellos estaban totalmente de acuerdo, de acuerdo, inseguros, en desacuerdo o totalmente en desacuerdo con el enunciado.

Para evaluar el conocimiento matemático general y las destrezas, se administró un test estandarizado existente. Este incluyó 58 tareas de opción múltiple correspondientes a ocho sub-escalas: operaciones lógicas, conjuntos, relaciones, números, operaciones matemáticas, problemas, medida y geometría (Stinissen, Mermans, Tistaert y Vander Steene, 1985).

Con el fin de obtener un mejor entendimiento de los cambios cualitativos en los procesos resolutivos de los alumnos como consecuencia de la intervención, se seleccionaron tres parejas de niños de cada aula experimental (una pareja de alumnos con alta habilidad, una con mediana y una con baja) y se les solicitó antes y después de la intervención resolver cinco problemas nuevos y no rutinarios en pares de igual habilidad. Se grabó un video de estas parejas y luego se lo analizó con un esquema de marcación que incluía tres aspectos: 1) el resultado final del proceso resolutivo (correcto, incorrecto, error técnico de cálculo o sin respuesta); 2) el uso de las ocho estrategias heurísticas enseñadas en el programa, y 3) la frecuencia de ocurrencia de cuatro valiosas actividades autorreguladoras (por ejemplo, orientación, planificación, monitoreo y evaluación).

 Para evaluar la fidelidad de la implementación del ambiente de aprendizaje por parte de los profesores de las aulas experimentales, se grabaron videos de una muestra de cuatro lecciones representativas en cada aula y luego se los analizó en términos de un perfil de implementación. Este perfil contenía diez categorías de actividades de profesores que se los consideraron importantes para el éxito de la implementación del ambiente de aprendizaje y que, de alguna manera, correspondían a las diez directrices mencionadas en el anexo D (por ejemplo, ofrecer una buena orientación a la tarea; observar el trabajo en grupo y proveer la ayuda necesaria cuando se la requiera; demostrar la existencia de diferentes soluciones y métodos resolutivos apropiados para el mismo problema durante la discusión con la clase, etc.).

RESULTADOS

De acuerdo con los resultados del pre-test, post-test y test de retención, en comparación con el grupo de control, la intervención tuvo un efecto positivo significativo y estable (tamaño del efecto .31) en la actuación resolutiva de problemas del grupo experimental (ver figura 1).

   

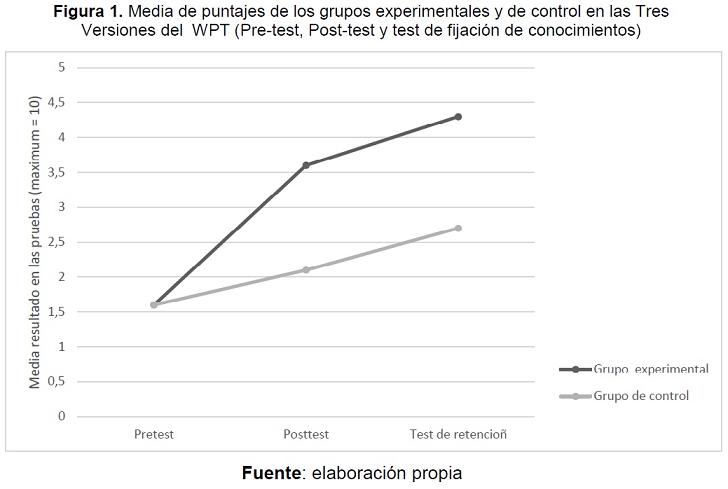
Los resultados de los cuestionarios indicaron que el ambiente de aprendizaje tuvo un impacto significativo positivo, aunque pequeño en relación al gusto y la persistencia de los niños en resolver problemas matemáticos y, en su perspectiva, orientado al proceso en la resolución de problemas (tamaño del efecto .04).

Los resultados del examen estandarizado de logros que cubría el currículo total de matemáticas mostraron que la atención extra a las estrategias cognitivas y autorreguladoras en las aulas experimentales no tuvo una influencia negativa en los logros de aprendizaje de otras partes del currículo (medida, geometría). Al contrario, hubo un efecto de transferencia reveladora y positiva;: los estudiantes de las aulas experimentales realizaron su trabajo significativamente mejor que los estudiantes de las aulas de control en este test (tamaño del efecto 0.38).

El análisis de las anotaciones de los estudiantes en sus hojas de respuestas en el post-test de problemas mostró que los mejores resultados del grupo experimental fueron determinadas por un incremento sustancial en el uso espontáneo de las destrezas heurísticas y autorreguladoras (orientación, planificación, monitoreo y evaluación) (tamaño del efecto .76). Este descubrimiento se confirmó con un análisis cualitativo de las entrevistas sobre resolución de problemas grabadas en los videos de las tres parejas de estudiantes de cada aula experimental, antes y luego de la intervención.

   

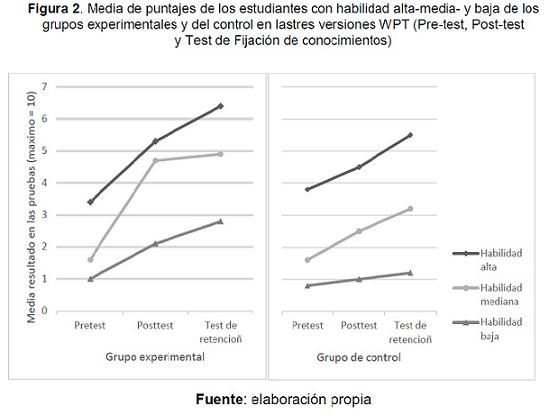
Finalmente, en las aulas experimentales no solamente los estudiantes con habilidad alta sino también aquellos de habilidad baja —aunque en grado pequeño— se beneficiaron de la intervención en todos los aspectos recientemente mencionados (ver figura 2)

CONCLUSIONES

Los resultados de este estudio apoyan la perspectiva de que, en un ambiente de aprendizaje CSSC, al combinar un conjunto de problemas diseñados de manera cuidadosa con métodos de enseñanza altamente activos y con la introducción de una nueva cultura de aula, se puede aumentar significativamente la competencia en la resolución de problemas matemáticos así como motivar el cambio en las creencias de los estudiantes sobre esta área. Un estudio realizado por Mason y Scrivani (2004) arroja los mismos resultados de esta investigación. Es interesante saber que los principios básicos aplicados en estas dos intervenciones convergen con las características de ambientes de aprendizaje efectivos que derivan de un reciente meta-análisis de experimentos de enseñanza: 1) entrenamiento integrado de estrategias cognitivas, metacognitivas y motivacionales usando una variedad de métodos de enseñanza; 2) atención explícita a la utilidad y beneficios de las estrategias; 3) creación de oportunidades para la práctica de las estrategias y provisión de retroalimentación sobre el uso de las estrategias, y 4) creación de una cultura de aula nueva a fin de estimular el aprendizaje autorregulado, especialmente la reflexión (Dignath y Büttner, 2008; Dignath, Buettner y Langfeldt, 2008; De Corte, Depaepe y Verschaffel, 2010; Veenman, Van Hout-Wolters y Afflerbach, 2006).

Implicaciones para la práctica y la política

Los resultados de este estudio de intervención sugieren que la concepción de aprendizaje CSSC puede guiar el diseño de novedosos pero también positivos ambientes de aprendizaje aplicables en la práctica, esto es: escenarios que posibiliten la adquisición de la competencia adaptativa (AC), particularmente destrezas heurísticas y de autorregulación. Es importante también anotar que la intervención arrojó un efecto sustentable: los profesores participantes continuaron aplicando este método innovador en la enseñanza de las matemáticas después de que la investigación terminó. Sin embargo, los efectos positivos de la intervención vinieron como resultado de una intensa colaboración y dirección de profesores y sus directores. Esto no es sorprendente. En efecto, la implementación efectiva y sustentable de ambientes de aprendizaje innovadores demanda mucho de los profesores y se requiere cambios sustanciales en su papel y práctica. En lugar de ser la principal fuente de información, el profesor se convierte en un miembro “privilegiado” de una comunidad de construcción del conocimiento cuya tarea es crear un clima de aula intelectualmente estimulante: modelar actividades de aprendizaje, pensamiento y de resolución de problemas; hacer preguntas provocadoras; ofrecer el apoyo a los estudiantes a través de entrenamiento y guía, y motivar y apoyar la autorregulación de los estudiantes para su propio aprendizaje. En otras palabras, el profesor provee la guía necesaria para el aprendizaje por descubrimiento.

En vista de la implementación de la concepción CSSC del aprendizaje, es interesante preguntarse si las ideas y creencias de los profesores y estudiantes convergen con esta perspectiva. Como punto de partida en la concepción de Erik De Corte (1995) sobre un aprendizaje efectivo como un proceso constructivo, acumulativo, autorregulado, orientado a una meta, situado y colaborativo de adquisición y construcción de conocimientos, John Berry y Pasi Sahlberg (1996) desarrollaron un instrumento para medir y analizar las ideas sobre el aprendizaje en estudiantes de 15 años en cinco escuelas en Inglaterra y Finlandia. La conclusión más importante del estudio fue que la mayoría de estudiantes se adhiere al modelo de aprendizaje como transmisión de conocimiento, que es difícil de acomodar a la concepción CSSC. Berry y Sahlberg concluyen que “las ideas de nuestros alumnos sobre el aprendizaje y la enseñanza reflejan las prácticas estáticas y cerradas de la escuela” (1996, 33). Añaden que esta conclusión se refleja en hallazgos similares de otros estudios de profesores y estudiantes adultos.

Estos hallazgos sugieren que las creencias acerca del aprendizaje pueden ser un obstáculo serio para la implementación del acercamiento al aprendizaje CSSC debido a que la historia de la educación muestra el arraigo profundo de prácticas de enseñanza (Berliner, 2008). Por lo tanto, cambiar estas creencias y prácticas en vista de la implementación sustentable y a gran escala de ambientes innovadores de aprendizaje basados en la concepción CSSC de aprendizaje es un reto para los profesionales de la educación, especialmente para el personal educativo a cargo y los artífices de las políticas. Se necesita un diseño o revisión del currículo y de los libros de texto que reflejen esta concepción. Sin embargo, la integración de nuevas ideas en los libros de texto no garantiza que estas sean usadas apropiadamente en la práctica (Depaepe, De Corte y Verschaffel, 2007). La investigación muestra que los profesores interpretan las ideas nuevas a través de experiencias pasadas (por ejemplo, Remillard, 2005) y, como lo demuestra Berry y Sahlberg (1996), los maestros con confían con frecuencia en las creencias tradicionales sobre el aprendizaje y la enseñanza. Más aún, como lo argumenta Cognition and Technology Group at Vanderbilt, los cambios requeridos son “demasiado complejos para ser comunicados sucintamente en un taller, y luego promulgados aisladamente una vez que los profesores retornan a sus escuelas” (1997: 116). Por lo tanto, existe la necesidad imperiosa de un aprendizaje profesional intensivo para autoridades escolares y profesores que abordan la “alta fidelidad” en la aplicación de ambientes de aprendizaje y materiales innovadores, mientras se centran en el cambio de percepciones y creencias predominantes sobre el aprendizaje. Tales cambios se facilitan por un proceso iterativo en el que las concepciones actuales sean desafiadas por el aprendizaje de prácticas alternativas exitosas (Timperley, 2008; National Research Council, 2000). En sus estudios para convertirse en profesores, los estudiantes deben estar inmersos en el tipo de ambientes de aprendizaje que se les aconseja crear y refinar en el futuro en sus propias aulas.

Finalmente, la implementación sustentable de la concepción CSSC requiere de una apropiada comunicación con ayuda de parte de la comunidad ampliada (Stokes, Sato, McLaughlin y Talbert, 1997) a fin de evitar lo que John Dewey (1916) llamó el aislamiento de la escuela. El apoyo de la comunidad ampliada es importante a fin de motivar sinergias entre el aprendizaje formal en el aula y el aprendizaje informal en las actividades fuera de la escuela (Bransford et al., 2006; National Research Council, 2000) y para el modelo descrito aquí para alcanzar su máximo potencial.

BIBLIOGRAFÍA

Alfieri, L., P.J. Brooks, N.J. Aldrich y H.R. Tenenbaum (2011). Does discovery-based instruction enhance learning? Journal of Educational Psychology 103, 1-18.

Bendixen, L.D. y Feucht F.C. (eds.) (2010) Personal epistemology in the classroom: Theory, research, and implications for practice. Cambridge, UK: Cambridge University Press.

Berliner, D.C. (2008). Research, policy, and practice: The great disconnect. En S.D. Lapan & M.T. Quartaroli (eds.) Research essentials: An introduction to designs and practices (pp. 295-325). Hoboken, NJ: Jossey-Bass.

Berry, J., & Sahlberg, P. (1996). Investigating pupils’ ideas of learning. Learning and Instruction, 6, 19-36.

Boekaerts, M., Pintrich, P.R. & Zeidner (eds.) (2000). Handbook of self-regulation. San Diego: Academic Press.

Bransford, J., Stevens, R., Schwartz, D., Meltzoff, A., Pea, R., Roschelle, J., Vye, N., Kuhl, P., Bell, P., Barron, B., Reeves, B., & Sabelli, N. (2006). Learning theories and education: Toward a decade of synergy. En P.A. Alexander & P.H. Winne (eds.) Handbook of Educational Psychology (2nd. ed.) (pp 209-244). Mahwah, NJ: Lawrence Erlbaum Associates.

Brown, A.L., & Campione, J.C. (1994). Guided discovery in a community of learners. In K. McGilly (ed.) Classroom lessons: Integrating cognitive theory and classroom practice (pp. 229-270). Cambridge, MA: The MIT Press.

Brown, A. L., & Palincsar, A. S. (1989). Guided, cooperative learning and individual knowledge acquisition. En L.B. Resnick (ed.) Knowing, learning and instruction. Essays in honor of Robert Glaser (pp. 393-451). Hillsdale, NJ: Erlbaum.

Brown, R., Pressley, M., Van Meter, P., & Schuder, T. (1996). A quasi-experimental validation of transactional strategies instruction with low-achieving second-grade readers. Journal of Educational Psychology, 88, 18-37.

Bruner, J.S. (1961). The act of discovery. Harvard Educational Review 31, 21-32.

Chi, M.T.H., Feltovich, P.J.,& Glaser, R. (1981). Categorization and representation of physics problems by experts and novices. Cognitive Science, 5, 121-125.

Chi, M.T.H., Glaser, R., & Farr, M.J. (1988). The nature of expertise. Hillsdale, NJ: Lawrence Erlbaum Associates.

Cognition and Technology Group at Vanderbilt (1997). The Jasper Project: Lessons in curriculum, instruction, assessment, and professional development. Mahwah, NJ: Lawrence Erlbaum Associates.

De Corte, E. (1995). Learning theory and instructional science. En P. Reiman & H. Spada (eds.) Learning in humans and machines. Towards an interdisciplinary learning science (pp. 97-108). Oxford, UK: Elsevier Science.

De Corte, E. (2003). Transfer as the productive use of acquired knowledge, skills, and motivations. Current Directions in Psychological Science, 12, 142-146.

De Corte, E. (2007). Learning from instruction: The case of mathematics. Learning Inquiry, 1, 19-30.

De Corte, E. (2010). Historical developments in the understanding of learning. En H. Dumont, D. Istance, & F. Benavides (eds.) The nature of learning. Using research to inspire practice (pp. 35-67). París: OECD Publishing.

De Corte, E., Depaepe, F., & Verschaffel, L. (2010). Fostering self-regulation skills in mathematics. En H. Pedrosa-de-Jesus, C. Evans, Z. Charlesworth & E. Cools (eds.) ELSIN XV, Proceedings of the 15^th Annual Conference of the European Learning Styles Information Network: Exploring styles to enhance learning and teaching in diverse contexts (pp. 133-139). Aveiro, Portugal: Universidade de Aveiro.

De Corte, E., Greer, B, & Verschaffel, L. (1996). Mathematics teaching and learning. En D.C. Berliner & R.C. Calfee (eds.) Handbook of educational psychology (491-549). New York, NY: Macmillan.

De Corte, E., Mason, L., Depaepe, F., & Verschaffel, L. (2011). Self-regulation of mathematical knowledge and skills. En B.J. Zimmerman & D.H. Schunk (eds.), Handbook of self-regulation of learning and performance (pp. 155-172). New York, NY: Routledge.

De Corte, E., & Verschaffel, L. (1987). The effect of semantic structure on first graders’ strategies for solving addition and subtraction word problems. Journal for Research in Mathematics Education, 18, 363-381.

De Corte, E., Verschaffel, L., & Masui, C. (2004). The CLIA-model: A framework for designing powerful learning environments for thinking and problem solving. European Journal of Psychology of Education, 19, 365-384.

De Corte, E., Verschaffel, L .& Op ‘t Eynde P. (2000). Self-regulation: A characteristic and a goal of mathematics education. En P. Pintrich, M. Boekaerts, & M. Zeidner (Eds.), Self-regulation: Theory, research, and applications (pp. 687-726). Mahwah, NJ: Lawrence Erlbaum Associates.

De Corte, E., Verschaffel, L., & Van de Ven, A. (2001). Improving text comprehension strategies in upper primary school children: A design experiment. BritishJournal of Educational Psychology, 71, 531-559.

Depaepe, F., De Corte, E., & Verschaffel, L. (2007). Unravelling the culture of the mathematics classroom: A video-based study in sixth grade. International Journal of Educational Research, 46, 266-279.

Dewey, J. (1916). Democracy and education. New York, NY: Macmillan.

Dignath, C., & Büttner, G. (2008). Components of fostering self-regulated learning among students. A meta-analysis on intervention studies at primary and secondary school level. Metacognition and Learning, 3, 231-264.

Dignath, C., Buettner, G, & Langfeldt, H. (2008). How can primary school students learn self-regulated learning strategies most effectively? A meta-analysis on self-regulation training programmes. Educational Research Review, 3, 101-129.

Ericsson, K.A. (2003). The acquisition of expert performance as problem solving: Construction and modification of mediating mechanisms through deliberate practice. In J.E. Davidson & R.J. Sternberg (eds.), The psychology of problem solving (pp. 31-83). Cambridge, UK: Cambridge University Press.

European Round-Table of Industrialists (ERT) (1995). Education for Europeans: Towards a learning society. Bruselas: ERT.

Garner, R. (1987). Metacognition and reading comprehension. Norwood, NJ: Ablex.

Hatano, G. (1996). A conception of knowledge acquisition and its implications for mathematics education. In L.P. Steffe, P. Nesher, P. Cobb, J. Kilpatrick, & B. Greer (eds.), Theories of mathematical learning (pp. 197-217). Mahwah, NJ: Lawrence Erlbaum Associates.

Hatano, G., & Inagaki, K. (1986). Two courses of expertise. En H. Stevenson, H. Azuma, & K. Hakuta (eds.), Child development and education in Japan (pp. 262-272). New York, NY: Freeman.

Hatano, G., & Oura, Y. (2003). Commentary. Reconceptualizing school learning using insightfrom expertise research. Educational Researcher, 32(8), 26-29.

Kirby, J.R., & Lawson, M.J. (2012). Enhancing the quality of learning. Dispositions, instruction, and learning processes. Cambridge, UK: Cambridge University Press.

Kirschner, P.A., Sweller, J., & Clark, R.E. (2006). Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching. Educational Psychologist, 41, 75-86.

Kirshner, D., & Whitson, J.A. (eds.) (1997) Situated cognition: Social, semiotic, and psychological perspectives. Mahwah, NJ: Lawrence Erlbaum Associates.

Lehtinen, E. (2003). Computer-supported collaborative learning: An approach to powerful learning environments. En E. De Corte, L. Verschaffel, N. Entwistle & J. van Merriënboer (eds.) Powerful learning environments: Unravelling basic componentsand dimensions (pp. 35-53). (Advances in Learning and Instruction Series.) Oxford, UK: Elsevier Science Ltd.

Mason, L., & Scrivani, L. (2004). Enhancing students’ mathematical beliefs: An intervention study. Learning and Instruction, 14, 153-176.

Mayer, R.E. (2004). Should there be a three-strikes rule against pure discovery learning? American Psychologist, 59, 14-19.

National Research Council. (2000). How people learn: Brain, mind, experience, and school. J.D. Bransford, A.L. Brown, & R.R. Cocking (eds.). Committee on Developments in the Science of Learning and Committee on Learning Research and Educational Practice. Washington, DC: National Academy Press.

National Research Council. (2005) How students learn: History, mathematics, and science in the classroom. Committee on How people learn, a targeted report for teachers, M.S. Donovan & J.D. Bransford (eds) Division of Behavioral and Social Sciences and Education. Washington, DC: National Academy Press.

Nunes, T., Schliemann, A.D., & Carraher, D.W. (1993). Street mathematics and school mathematics. Cambridge, UK: Cambridge University Press.

Piaget, J. (1955). The child’s construction of reality. London, UK: Routledge and Kegan Paul.

Picker, S.H., & Berry, J.S. (2000). Investigating pupils’ images of mathematicians. Educational Studies in Mathematics, 43, 65-94.

Remillard, J.T. (2005). Examining key concepts in research on teachers’ use of mathematics curricula. Review of Educational Research, 75, 211-246.

Salomon, G. (Ed.). (1993). Distributed cognition. Psychological and educational considerations. Cambridge, UK: Cambridge University Press.

Salomon, G., & Perkins, D.N. (1998). Individual and social aspects of learning. En P.D. Pearson & A. Iran-Nejad (eds.), Review of research in education (vol. 23, pp. 1-24). Washington, DC: American Educational Research Association.

Scardamalia, M., Bereiter, C., & Steinbach, R. (1984). Teachability of reflective processes in written composition. Cognitive Science, 8, 173-190.

Schmidt, H.G., Loyens, S.M.M., van Gog, T., & Paas, F. (2007). Problem-based learning is compatible with human cognitive architecture: Commentary on Kirschner, Sweller, and Clark (2006). Educational Psychologist, 42, 91-97.

Schoenfeld, A.H. (1985). Mathematical problem solving. New York, NY: Academic Press.

Schoenfeld, A.H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense-making in mathematics. En D.A. Grouws (ed.), Handbook of research on mathematics teaching and learning (pp. 334-370). New York, NY: Macmillan.

Schommer, M. (1994a). An emerging conceptualization of epistemological beliefs and their role in learning. En R. Garner & P. Alexander (Eds.), Beliefs about text and about text instruction (pp. 25-39). Hillsdale, NJ: Lawrence Erlbaum Associates.

Schommer, M. (1994b). Synthesizing epistemological beliefs research: Tentative understandings and proactive confusions. Educational Psychology Review, 6, 293-319.

Schraw, G. (2006). Knowledge structures and processes. En P.A. Alexander & P.H. Winne (Eds.), Handbook of educational psychology. (2nd. ed.) (pp. 245-263). Mahwah, NJ: Lawrence Erlbaum Associates.

Sfard, A. (1998).On two metaphors for learning and the dangers of choosing just one. Educational Researcher, 27(2), 4-13.

Simons, R.J., van der Linden, J., & Duffy, T. (Eds.). (2000). New learning. Dordrecht, The Netherlands: Kluwer Academic Publishers.

Slavin, R.E. (2010). Co-operative learning: What makes group-work work? En H. Dumont, D. Istance, & F. Benavides (eds.), The nature of learning. Using research to inspire practice (pp. 161-178). París: OECD Publishing.

Stinissen, J., Mermans, M., Tistaert, G. & Vander Steene, G. (1985). Leuvense Schoolvorderingentest Vernieuwde Wiskunde 2-6. [Leuven Standard Achievement Test New Mathematics 2-6] Brussel: C.S.B.O.

Songer, N.B., & Linn, M.C. (1991). How do students’ views of science influence knowledge integration? Journal of Research in Science Teaching, 28, 761-784.

Stokes, L.M., Sato, N.E., McLaughlin, M.W., & Talbert, J.E. (1997). Theory-based reform and problems of change: Contexts that matter for teachers' learning and community. Stanford, CA: Center for Research on the Context of Secondary Teaching, School of Education, Stanford University.

Timperley, H. (2008). Teacher professional learning and development. (Educational Practices Series, 18). Geneva, CH: International Bureau of Education.

Veenman, M. V. J., Van Hout-Wolters, B. H. A. M., & Afflerbach, P. (2006). Metacognition and learning: Conceptual and methodological considerations. Metacognition and Learning,1, 3-14.

Verschaffel, L., De Corte, E., Lasure, S., Van Vaerenbergh, G., Bogaerts, H., y Ratinckx, E. (1999). Learning to solve mathematical application problems: A design experiment with fifth graders. Mathematical Thinking and Learning, 1, 195-229.

Wineburg, S. (1991). Historical problem solving: A study of the cognitive processes used in the evaluation of documentary and pictorial evidence. Journal of Educational Psychology, 83, 73-83.

Wood, T., Cobb, P., & Yackel, E. (1991). Change in teaching mathematics: A case study. American Educational Research Journal, 28, 587-616.

Yackel, E., & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for Research in Mathematics Education, 27, 458-477.

Zimmerman, B.J. (1994). Dimensions of academic self-regulation: A conceptual framework for education. En D.H. Schunk & B.J. Zimmerman (eds.), Self-regulation of learning and performance: Issues and educational applications (pp. 3-21). Hillsdale, NJ: Lawrence Erlbaum Associates.

Zimmerman, B.J., & Risemberg, R. (1997). Self-regulatory dimensions of academic learning and motivation. En G.D. Phye (Ed.), Handbook of academic learning: Construction of knowledge (pp. 105-125). San Diego, CA: Academic Press.

Zimmerman, B.J., & Schunk, D.H. (eds.). (2011). Handbook of self-regulation of learning and performance. New York, NY: Routledge.

ANEXOS

Anexo A. Cuatro viñetas ilustran las características de un aprendizaje efectivo

Viñeta 1

Solución de una resta simple realizada por un alumno de primaria

543

     - 175

---------

432

¿Cómo realizó el alumno esta resta?

Viñeta 2

(Tomado de Nunes, Schliemann & Carraher, 1993)

Alguien compra a un vendedor ambulante, de 12 años, en Recife, Brasil, 10 cocos a 35 cruzeiros cada uno. El muchacho calcula rápida y exactamente el precio de la siguiente manera “3 cocos son 105; 3 más son 210; …tengo que añadir 4, que hacen… 315 …Son 350 cruzeiros.”

Cuando el muchacho tenía que resolver problemas tradicionales de un texto en la escuela, lo hacía más mediocremente que cuando estaba en su negocio en la calle. En clases él no usaba los procedimientos que los utilizaba tan rápidamente en la calle, pero él intentaba aplicar los algoritmos aprendidos en la escuela que aparentemente no los manejaba muy bien.

Viñeta 3

En relación a los eventos en Kosovo, un proyecto que se enfocaba en el estudio de la situación en los Balcanes se estableció en una clase de 25 estudiantes del tercer año de secundaria. Un alumno en la clase tenía un historial étnico albanés. Sus padres migraron pocos años antes de Kosovo a Belgica. En la primera fase del proyecto se dividió a la clase en cinco “grupos de investigación”, con cinco alumnos en cada uno. Cada grupo estudió a los Balcanes desde diferentes perspectivas:

• Grupo 1: perspectiva política

• Grupo 2: perspectiva social

• Grupo 3: perspectiva económica

• Grupo 4: perspectiva cultural

• Grupo 5: perspectiva religiosa

Cuando los grupos de investigación hicieron su trabajo, luego de algunas sesiones, la clase fue reorganizada en “grupos de aprendizaje”. En cada grupo había un representante de cada grupo de investigación que llevó a combinar y discutir los conocimientos de las cinco perspectivas haciendo posible que todos los alumnos estuvieran aprendiendo acerca de la situación global y los problemas de los Balcanes.

Anexo B. El modelo de competencia resolutiva de problemas subyacente al Ambiente de Aprendizaje.

PASO 1: CONSTRUYA UNA REPRESENTACIÓN MENTAL DEL PROBLEMA

Heurística: Haga un dibujo.

Haga una lista, un esquema o una tabla.

Distinga datos relevantes e irrelevantes.

Use su conocimiento real del mundo.

PASO 2: DECIDA CÓMO SOLUCIONAR EL PROBLEMA

Heurística: Haga un cuadro de flujos.

Adivine y compruebe.

Busque un patrón.

Simplifique los números.

PASO 3: HAGA LOS CALCULOS NECESARIOS

PASO 4: INTERPRETE EL RESULTADO Y FORMULE UNA RESPUESTA

PASO 5: EVALUE LA SOLUCIÓN

Anexo C. Problema de un viaje escolar

El profesor informó a los niños acerca de un plan para un viaje escolar para visitar el Efteling, un parque de diversiones muy conocido en Holanda, pero si este resultaba muy costoso, algún otro parque podría ser una alternativa. Cada grupo, de cuatro estudiantes, recibió copias de folders con los precios de entrada a cada parque. La lista incluía distintos precios dependiendo de la época del año, la edad de los visitantes y el tipo de grupo (personas individuales, familias, grupos). Adicionalmente, cada grupo recibió una copia de un fax de una empresa de buses locales dirigida al director de la escuela. El fax contenía información con el precio, de acuerdo con el tamaño del bus (con chofer), por un viaje de un día hacia el Efteling.

La primera tarea de los grupos fue comprobar si era posible hacer el viaje al parque Efteling, bajo la premisa de que el precio máximo por niño era de 12, 50 euros. Después de descubrir que éste no era posible, el grupo recibió una segunda tarea; tenían que descubrir cuál de los otros parques podrían visitar con la suma de 12,50 euros.

Anexo D. Lineamientos generales para los profesores antes, durante y después de trabajos grupales e individuales

ANTES

1. Relacione el nuevo conocimiento a lo ya aprendido (heurística, paso de solución de problema)

2. Dé una buena orientación a la tarea nueva.

DURANTE

3. Observe el trabajo grupal y ofrezca sugerencias apropiadas cuando se necesite.

4. Estimule la articulación y la reflexión.

5. Estimule un pensamiento activo y cooperativo de todos los miembros (especialmente de los más débiles/tímidos)

DESPUÉS

6. Demuestre la existencia de soluciones y métodos diferentes para el mismo problema.

7. Evite imponer a los estudiantes soluciones y métodos de solución.

8. Ponga atención a las destrezas heurísticas y autorreguladoras del modelo de resolución de problemas previstas y use el modelo como base para la discusión.

9. Estimule la participación activa de tantos estudiantes como sea posible para la discusión de clase.

10. Indique aspectos positivos y negativos de la dinámica de grupo.