Services on Demand
Journal
Article
Related links
Share
CLEI Electronic Journal
On-line version ISSN 0717-5000
CLEIej vol.17 no.2 Montevideo Aug. 2014
Abstract
In a group of individuals that come together to produce a good or provide a service, the cooperators (who pay to produce the good) are often exploited by those who receive the benefit without paying the cost. Models were developed over time using incentives (reward or punishment) and the option of abandoning the initiative to promote and stabilize the cooperation.
In this paper we analyze several models based on the evolutionary game theory and public good games. We compare and organize them in a taxonomic table following their main characteristics to select the most suitable for a specific problem.
The analyzed models are compared by using a public good problem in community projects for water supply. We have reasonable assurance that phenomena that appear on models also occurs in these community projects. Therefore, we propose that evolutionary game theory can be a useful tool for policy-makers in order to improve cooperation and discourage defection in sanitation boards.
Spanish Abstract:
En un grupo de individuos que se unen para producir un bien o proveer un servicio, los cooperadores que pagan el costo de producir el bien a menudo son explotados por aquellos que sin aportar reciben de igual forma el beneficio. Diversos modelos fueron desarrollados a lo largo del tiempo, que utilizan incentivos (premios o castigos) y la opción de no participar en la iniciativa para favorecer y estabilizar la cooperación. En este trabajo se analizan varios modelos que utilizan como marco la teoría de juegos evolutivos y los juegos de bienes públicos. Comparamos y sistematizamos los modelos en una tabla de acuerdo a características principales de forma a seleccionar los más adecuados en función de un problema específico. Los modelos analizados son comparados utilizando el problema del bien público en proyectos comunitarios de aprovisionamiento de agua potable. Tenemos indicios razonables de que los fenómenos que aparecen en los modelos también ocurren en los proyectos comunitarios. Por lo tanto, proponemos la teoría de juegos evolutivos como una herramienta útil para los tomadores de decisiones a fin de incrementar la cooperación y desalentar la deserción en las juntas de saneamiento.
Keywords: Evolutionary game theory, evolution of cooperation, public good game, sanitation board.
Spanish Keywords: Teoría de juegos evolutivos, evolución de la cooperación, juegos de bienes públicos, juntas de saneamiento.
Received 2013-11-15, Revised 2014-02-20, Accepted 2014-02-20
In 1973, J. Maynard Smith and G. R. Price published “The Logic of Animal Contest” [1] to explain the logic behind the ritualized contest among animals. At that time, group selection (see Definition 1) was the well-known explanation for this behavior. According to this, natural selection favors behaviors and traits that benefit the group or specie over the individual. However, [1] proved that ritualized contests can be beneficial from the individual point of view. This article was the beginning of the evolutionary game theory.
To represent the conflict, [1] developed a model for the contest where each animal can use two types of tactics: either dangerous or conventional. With dangerous tactics the animal inflicts serious injury in the opponent, but with conventional tactics he does not. They proposed five different strategies and characterized which one was stable under natural selection: an evolutionary stable strategy - ESS (see Definition 2 in §2.2).
The evolutionary game theory -EGT- has elements that come from game theory [2] and natural selection theory [3]. To apply game theory in a biological context of conflict and cooperation, it is necessary to replace “utility” by “fitness” (see Definition 3) and “rationality” by “natural selection” [4]. One importante difference between both approaches consists in the fact that unlike classic game theory, EGT does not deal with individuals that take rational decisions. Conversely, EGT deals with populations of individuals, and the natural selection process defines if a strategy (trait or behavior) either survives or disappears. Strategies with higher payoffs are stimulated by natural selection and spread within the population by imitation, learning or inheritance [5].
The payoff of a strategy is defined by the action of each individual player with respect to the actions chosen by the others in the population; therefore, it depends on all frequencies of the strategies within the population. Since these frequencies change in accordance to the payoffs, this leads to a feedback loop. The dynamic of the loop rely on the population structure, the game and the way strategies spread out[5].
Although, in [1] the concept of ESS was introduced by defining a stable state of a game. Only a few years later, Taylor and Jonker [6] proposed a dynamic for the game, so-called “replicator dynamics”. In this dynamic, the frequencies of the strategies evolve according to the difference between the strategy’s payoff and the population’s average payoff. Strategies with payoff higher than the average population payoff will increase in frequency, meanwhile strategies with payoff lower than average population payoff will decrease in frequency.
Later on, other dynamics were developed; e.g. “imitation dynamics”, “best response dynamics”, “smoothed best reply dynamics” or “Brown - von Neumann - Nash dynamics” [5]. The models, studied in this work, use “replicator dynamics”.
1.2 The evolution of cooperation
The origin and the evolution of cooperation is still an enigma that has fascinated evolutionary biologist for a long time. On one hand, cooperation implies the individual voluntarily resign from part of her fitness for the benefit of the group; on the other hand, natural selection is a competitive process that ensures the survival of the fittest. In this context, how does the cooperation appear and be maintained?
In 1971, [7] related the cooperation with game theory when suggested that the association between two individuals exposed repeatedly to symmetric and reciprocal situations, is analogous to the Prisoner’s Dilemma [8]. Afterwards, in 1981,“The Evolution of Cooperation” [9] analyzed the evolution of cooperation modeling direct reciprocity through iterated prisoner’s dilemma. Two computer tournaments were organized to find a strategy able to sustain cooperation in iterated prisoner’s dilemma. In both cases the winner strategy was tit-for-tat.
However, the ability of tit-for-tat to maintain the cooperation decreases considerably if there is more than two players. In this sense, Public Good Games (PGG) or 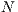 -person-prisoner’s dilemma was used to study cooperation in a group of unrelated individuals. Within these problems, incentives (rewards or punishment) and the option of leaving the initiative, were two mechanisms proposed to promote and stabilize the cooperation. Several models were developed by using one or both of them ([10, 11, 12, 13, 14, 15]).
-person-prisoner’s dilemma was used to study cooperation in a group of unrelated individuals. Within these problems, incentives (rewards or punishment) and the option of leaving the initiative, were two mechanisms proposed to promote and stabilize the cooperation. Several models were developed by using one or both of them ([10, 11, 12, 13, 14, 15]).
In this paper we analyze several models and homogenize their definitions (see §2.2). In §3 the models are replicated and phase diagrams are reproduced for each of them. We present a Table that systematizes their characteristics helping to select those more suitable for a specific problem. In §3.2,we select three models to analyze the cooperation in Sanitation Boards (SBs) for water supply. We observed that some behaviors (e.g. cycles) resulting from the EGT models can be seen in SBs. Therefore, using these models with real data, we expose how EGT can be a useful tool for policy-makers in order to improve cooperation and discourage defection.
In this section, we introduce the background of EGT, definitions and the models to be analyzed in this work. The models are sorted in a chronological order to show the evolution in modeling the cooperation. All models use Public Good Games -PGG (see Definition 4 below)- as paradigm with the replicator dynamic and non-structured populations.
The existence of cooperation can be explained under certain circunstantes such as kin selection [16], direct reciprocity [7, 9], indirect reciprocity [17] and the structure of the population [18]. Every model has working conditions; for instance, direct reciprocity requires repetitive interactions and a small group of participants; kinship is based in some genetic relationship; indirect reciprocity requires the knowledge of the reputation of all participants; and structured population requires that each participant is positioned such that the interaction is performed always with the same participants.
What happens when the conditions mentioned above are not satisfied?; for instance, under situations with large populations, without any internal spatial population structure and no-kinship between the participants. In these kind of games, the rational option consists in to defect (defectors) and exploit the contribution of the others participants (cooperators). But if all participants are defectors, the result is economic stalemate and as a consequence, at the end of the game all participants are losers. At the literature, this result is known with different denominations such as social dilemma (see Definition 5), tragedy of the commons [19, 20], free-rider problem and social trap [10].
In order to avoid social dilemma, defectors are normally punished; however, in this case punishers have to contribute to both the game and the punishment. In PGG experiments, it can be observed an increment of the cooperation (and vice versa) if a punishment is introduced into the game [21]. This happens even in the case, when the participants do not return to the same group, and therefore, they would not receive any profits for a future contribution of the former defectors. For this reason, this kind of behavior is known as altruistic punishment (see Definition 6).
The punishment improves the contribution to the game producing a profit for all participants. Hence, the punishment system itself can be defined as a public good, and it can be exploited for cooperators (second order exploiters). The rational option consists in cooperating without punishing since the payoff of cooperators is higher; but if the punishers disappear the game returns to the initial condition where the contribution decreases and the cooperation disappears. The solution would be to apply the punishment to defectors (first order exploiters) as well as cooperators (second order exploiters); however in this case it could appear third order exploiters an so on [22].
The most common punishment systems in the evolution of the cooperation are: Peer-punishment (see Definition 7) and pool-punishment (see Definition 8). Peer-punishment is equivalent to the situation when people take the law into their hands and punish those who do not cooperate. Conversely, pool-punishment is considered as an institutionalization to defend the common good [22].
Although most PGG with punishment experiments are based on peer-punishment, this mechanism has limitations [23]. On one hand, a minority of punishers must pay a high cost to impose sanctions on a group composed mostly of defectors, and under these conditions, punishers can not invade the population. On the other hand, in a group where all are contributors, punishers and cooperators have the same payoff (since there is no one to punish) and cooperators can increase the population up to a point when defectors appear again, punishers are no longer sufficient to resist the invasion.
If punishers can not invade but can be invaded, how it can be explained the emergence and maintenance of punishment in a population? This question has evolved from how cooperation arises to how altruistic punishment arises [23].
When pool punishment is considered, there exists the same problem for explaining how it arises and maintains the punishment. In fact, it is less efficient since it must introduce the maintenance of the penalty system in the punishment cost even if there are not defectors [23]. The advantage is in the second order punishment (the punishment of cooperators that do not punish). While in peer-punishment is no possible to recognize the punishers from the non-punishers until the end of the game; in the context of pool punishment, the participant has to declare ex-ante its behavior. This yields a more efficient second order punishment system [23].
In the same way of punishing defectors, it is possible to reward cooperators. Although, the importance of using positive (reward) or negative (punishment) incentive is well-known in social sciences, rewarding as a mechanism of maintaining cooperation has not been extensively analyzed [24].
Depending on the circumstances the strategies can be more efficient. For instance, when there is a considerable amount of defectors and few cooperators, the punishment is expensive but reward is cheap. On the contrary, when there is a large number of cooperators and few defectors, punishment is cheap but reward is expensive. Following this reasoning, an appropriate strategy to transform a group of defectors in cooperators would be to use initially a rewarding approach and afterward a punishment system [24].
Similarly to the punishment, reward can be implemented in two ways: pool-rewarding and peer-rewarding, depending on the decision of implementing the rewarding. Hence, the reward becomes a public good when profits cooperators, but it is expensive for rewarders. As a consequence, rewarders can be exploited by cooperators becoming second order exploiters.
Another important factor is the voluntary participation in the game. Those who decide not to participate are known as loners. The option to leave the PGG avoids the prisoner dilemma in cases when defectors dominate the population. Thus, the option of abandoning the game yields a continuously emerging of cooperation in the population [10], arising in a rock-scissor-paper cycle.
If a group is composed mostly of cooperators, defectors have a higher payoff. If defectors are predominant, loners have higher payoff. If almost all leave the game, the PGG is minimized until it does not constitute a social dilemma. In this case, cooperators have a higher payoff. This result was proved experimentally by [25].
In last years, it has been researched the effect of combining incentives with the option of abandoning the game [23, 15]. It was found that it is easier to reach the cooperation in a voluntary game than in a compulsory one. The option of abandoning the game avoids the dominance of defectors and maintain the cooperation over the time. The implementation of incentives increments the percentage of cooperators in the group at the same time of preventing the presence of exploiters.
Next we introduce the definitions used for modeling in this work.
Definition 1 Group selection: This form of selection assumes that natural selection acts both to the individual level and to the group level [26]. In group selection, there is a competition to survive between groups; therefore, those with better fitness survive and those with worse fitness have the tendency to disappear.
Definition 2 Evolutionary stable strategy (ESS): A strategy is denoted as evolutionary stable if all members in the population adopt the strategy and it can not be invaded by an alternative strategy [4].
Definition 3 Fitness: It is the genetic contribution of an individual to future generations, with respect to contributions of the other members of the population [27].
Definition 4 Public good game (PGG): It occurs when two or more persons (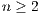 ) create a group for a project. Each participant receives a specific amount
) create a group for a project. Each participant receives a specific amount 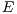 of money and has to decide, simultaneously with the others participants, which part of the received amount will bring to the project. The collected money is multiplied by a factor
of money and has to decide, simultaneously with the others participants, which part of the received amount will bring to the project. The collected money is multiplied by a factor 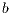 with
with 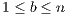 which yields the income of the project and it is distributed equally between the
which yields the income of the project and it is distributed equally between the 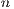 members of the group without any discrimination about the amount of the contribution [28].
members of the group without any discrimination about the amount of the contribution [28].
In PGG, each participant receives 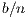 for its contribution to the project. However, since
for its contribution to the project. However, since 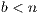 only a fraction of the contribution is recovered, the rational choice consists in the no-contribution strategy, but receiving the benefits of the contribution of the other participants. Unfortunately, if all participants have the same behavior, then none improve its initial contribution. The prisoner’s dilemma is a particular case of PGG with
only a fraction of the contribution is recovered, the rational choice consists in the no-contribution strategy, but receiving the benefits of the contribution of the other participants. Unfortunately, if all participants have the same behavior, then none improve its initial contribution. The prisoner’s dilemma is a particular case of PGG with 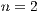 where the player has two option: to cooperate (contribute) or defect (no-cooperate). Depending on the option of participation, the PGG can be either voluntary (VPGG) or compulsory (CPGG). For instance, global environmental problems are compulsory.
where the player has two option: to cooperate (contribute) or defect (no-cooperate). Depending on the option of participation, the PGG can be either voluntary (VPGG) or compulsory (CPGG). For instance, global environmental problems are compulsory.
Definition 5 Social dilemma: It is defined by two properties: (a) the payoff of each participant for defecting is larger than the payoff for cooperating independently of the behavior of the other participants. In this case, defecting is the dominant strategy in the game. (b) if all participants defect, they obtain a lower payoff than if all cooperate. For instance, over exploitation and contamination are social dilemmas [29].
Definition 6 Altruistic punishment: It occurs when the punishment is expensive for the punisher and it does not bring any benefit to itself.
Definition 7 Peer-punishment: It is the action of deciding and applying a punishment to the exploiters after the distribution of the benefit to the participants in a PGG [23].
Definition 8 Pool-punishment: It is the action of deciding ex-ante the PGG, if a player contributes or not to a pool that will be use to punish exploiters [23].
In this article, we use the “replicator dynamics”. In this dynamic the natural selection depends on the frequency of an infinite population without mutation. The frequency of a strategy varies as the difference between its payoff and the average population payoff, and it is described by [30]:
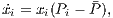 | (1) |
where 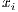 is the frequency of strategy
is the frequency of strategy 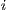 and
and 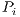 is its payoff.
is its payoff. 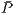 represents the population’s average payoff given by
represents the population’s average payoff given by 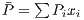 , and
, and 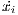 denotes the growth rate of the strategy
denotes the growth rate of the strategy 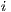 .
.
Model 1. In [10], the game is voluntary. There are three strategies: cooperators “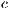 ”, defectors “
”, defectors “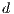 ” and loners “
” and loners “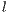 ”. Their expected payoffs are
”. Their expected payoffs are
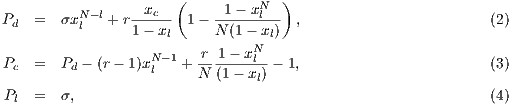
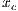 ,
, 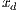 and
and 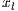 represent the frequencies of each strategy (cooperators, defectors and loners, respectively) with the condition of
represent the frequencies of each strategy (cooperators, defectors and loners, respectively) with the condition of 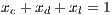 ;
; 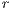 is the multiplication factor and
is the multiplication factor and 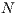 is the sample group of players randomly chosen to participate in the game. Loners have a fixed payoff
is the sample group of players randomly chosen to participate in the game. Loners have a fixed payoff 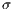 that does not depend on the others payoff. If only one participant decides to play, its payoff is the same as a loner.
that does not depend on the others payoff. If only one participant decides to play, its payoff is the same as a loner. It is assumed that 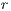 is greater than 1; thus, if all the players cooperate, they would have a higher payoff than if all the players defect. It is also assumed the payoff of loners is lesser than the payoff of the cooperative group, but greater than the payoff of the defectors group (
is greater than 1; thus, if all the players cooperate, they would have a higher payoff than if all the players defect. It is also assumed the payoff of loners is lesser than the payoff of the cooperative group, but greater than the payoff of the defectors group (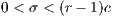 ). The cost of contributing
). The cost of contributing 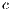 is normalized to 1 [10].
is normalized to 1 [10].
The three strategies generate a cycle of rock-scissor-paper type, where cooperators are invaded by defectors, defectors are invaded by loners and loners are invaded by cooperators, closing the cycle.
When loners are included in PGG, defectors can no longer dominate the population and cooperation subsists (at least to some proportion) over the time. The rock-scissor-paper cycle in voluntary PGG was verified experimentally in [25].
Model 2. In Model 1, the three strategies coexist; neither defectors nor cooperators dominate the population. One way to strengthen the cooperation is to include a fourth strategy, the punishers, “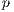 ” with the purpose of punishing defectors and cooperators who do not punish. According to this model [11], punishment can emerge in a population where individuals have no incentive to contribute or to punish those who do not contribute. The punishers enter and dominate the population of cooperators, defectors and loners. The payoffs of the strategies are defined by:
” with the purpose of punishing defectors and cooperators who do not punish. According to this model [11], punishment can emerge in a population where individuals have no incentive to contribute or to punish those who do not contribute. The punishers enter and dominate the population of cooperators, defectors and loners. The payoffs of the strategies are defined by:
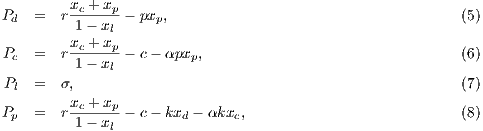
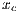 ,
, 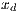 ,
, 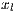 and
and 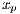 are cooperators, defectors, loners and punishers frequencies, respectively. In addition
are cooperators, defectors, loners and punishers frequencies, respectively. In addition 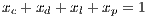 ;
; 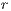 represents the multiplication factor,
represents the multiplication factor, 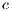 is the cost of the contribution of cooperators and punishers to the game,
is the cost of the contribution of cooperators and punishers to the game, 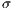 is the payoff of loners and
is the payoff of loners and 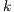 is the cost of performing the punishment
is the cost of performing the punishment 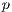 .
. Defectors and cooperators (second order exploiters) are punished, but the punishment of the cooperators is a fraction 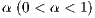 of the punishment of the defectors. All parameters are positives, the profit to the group of an individual contribution must be greater than the payoff of a loner (
of the punishment of the defectors. All parameters are positives, the profit to the group of an individual contribution must be greater than the payoff of a loner (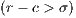 ) and the punishment is larger than the cost
) and the punishment is larger than the cost 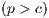 [11].
[11].
The punishers can increase its frequency by having a better payoff. In [11], it was suggested that with the evolution of the punishment, the rock-scissor-paper cycle, existent in voluntary PGG (VPGG), should disappears.
As mentioned in [11], some objections were presented to this model. For instance, second order punishment is not common in laboratory experiments and a group of punishers can be invaded by punishers who punish less (lower 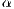 ).
).
Model 3. This model [12] questions the result obtained by Model 2, where the punishers get into the population and dominate it. This occurs because the model allows a single participant to play the PGG, the payoff obtained by this participant is larger than a payoff of loners and equal to the one obtained for a group of cooperators. Thus, either a single cooperator or a single punisher can invade a population of loners [12]. To take into account these cases, this model uses the terms 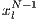 and
and 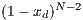 into the following payoffs:
into the following payoffs:
![N- 1 Pd = σxl + r(xc + xp)FN (l) - βxp (N - 1), (9) Pc = σxNl- 1+ (r- 1)(1 - xNl-1)- rxdFN (l)- αβxp(N - 1)[1 - (1 - xd)N -2], (10) Pl = σ, (11) P = σxN- 1+ (r- 1)(1 - xN -1)- rx F (l)- αγx (N - 1)[1 - (1 - x)N -2]- γx (N - 1), (12) p l l d N c d d](/img/revistas/cleiej/v17n2/2a0749x.png)
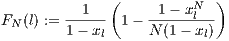 | (13) |
where 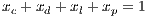 .
.
If only one player accepts to participate, he would receive a payoff similar to a loner. Punishers reduce the payoff of defectors by 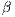 at a personal cost of
at a personal cost of 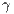 . They also reduce the payoff of cooperators by
. They also reduce the payoff of cooperators by 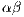 at
at 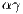 personal cost. It is assumed that cost
personal cost. It is assumed that cost 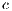 is equal to 1, that
is equal to 1, that  and that
and that 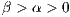 .
.
This model shows a bistable behavior, depending on the initial conditions, the system converges to a Nash equilibrium with cooperators and punishers or a state where the punishers disappear, and therefore, the cycle of cooperators, loners and defectors returns [12].
Model 4. This model [13] implements the combined effects between voluntary participation and punishment. Two configurations are presented: infinite and finite population. In this sense, there are four strategies: cooperators “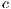 ”, defectors “
”, defectors “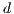 ”, loners “
”, loners “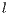 ” and punishers “
” and punishers “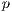 ”. There is a sample group of
”. There is a sample group of 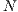 individuals. Cooperators, defectors and punishers accept to participate. Loners refuse to participate and receive a fixed independent payoff
individuals. Cooperators, defectors and punishers accept to participate. Loners refuse to participate and receive a fixed independent payoff 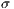 . If only one participant accepts to participate his payoff would be reduced to that of a loner. The contribution to the game is
. If only one participant accepts to participate his payoff would be reduced to that of a loner. The contribution to the game is 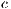 . Punishers impose a
. Punishers impose a 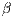 penalty to defectors with a
penalty to defectors with a 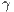 cost to themselves (
cost to themselves (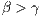 ). Penalties to cooperators are reduced to
). Penalties to cooperators are reduced to 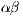 and the cost to
and the cost to 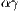 where
where 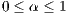 [13].
[13].
It is assumed that the payoff of loners is less than the payoff of the group of cooperators, but more than the group of defectors 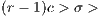 0. To analyze the origin and evolution of cooperation, when there is a social dilemma, the factor
0. To analyze the origin and evolution of cooperation, when there is a social dilemma, the factor 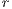 must be less than
must be less than 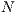 , otherwise, the best option is always to cooperate [13].
, otherwise, the best option is always to cooperate [13].
Infinite population. For the infinite population case, replicator dynamics is used. Following, strategies payoffs are defined by:
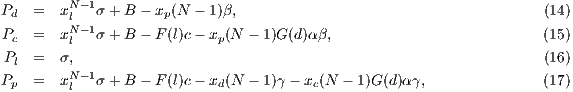
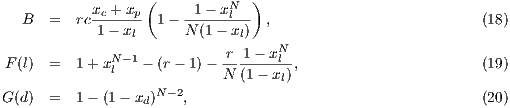
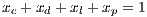 ;
; 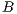 denotes the average return for defectors,
denotes the average return for defectors, 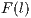 represents the difference in payoffs before the punishment between contributors (cooperators and punishers) and defectors. The probability to find and punish cooperators (who do not punish) is given by
represents the difference in payoffs before the punishment between contributors (cooperators and punishers) and defectors. The probability to find and punish cooperators (who do not punish) is given by 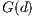 [13].
[13]. Finite population. The analysis of finite populations is based on Moran process [31]. It is used to describe biology processes. It consists of randomly selecting an individual from a population with a probability proportional to its fitness. This individual produces a clone in the population that replace another randomly selected individual regardless of their fitness.
According to [13], Moran process can be understood in some contexts as an imitation process, where an individual randomly selected adopts the strategy of another individual selected with a probability proportional to their fitness and where mutations correspond to individuals that experiments randomly with different strategies.
In the game, 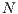 individuals are randomly selected from a population of size
individuals are randomly selected from a population of size 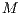 where
where 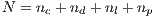 and
and 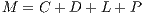 . The probability to interact in a group of
. The probability to interact in a group of 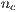 cooperators,
cooperators, 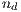 defectors,
defectors, 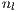 loners and
loners and 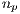 punishers is given by [13]:
punishers is given by [13]:
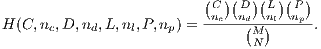 | (21) |
In a group of size 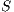 , (
, (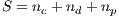 ) the average payoff of each strategy are given by:
) the average payoff of each strategy are given by:
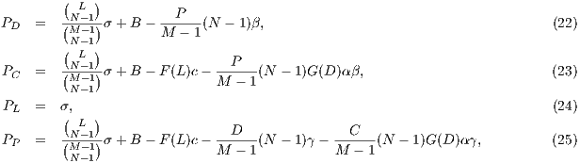
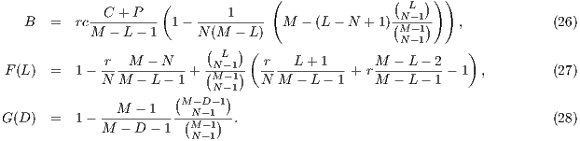
If a population is composed exclusively by loners, the system can either change to the state of cooperation or punishment with equal probability [13]. When the number of participants is small there is a possibility that by chance, the group is being composed of cooperators or punishers. Since both strategies have better payoffs the behavior is imitated by others players of the population.
The difference is that a population consisting mostly of cooperators is easily invaded by defectors, and as a result the cycle of cooperators, defectors and loners reappears. But a population with mostly punishers is more stable, it can only be exploited by cooperators (second order exploiters)[13].
Model 5. Under certain circumstances, it is not possible for the player to abandon the game. In this case the public good game become compulsory (CPGG). Examples of CPGG are environmental problems such as contamination and natural resources over-exploitation. In [14], a CPGG was modeled using a reward fund as a mechanism to maintain cooperation.
Three strategies are considered in this model, rewarders “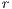 ”, cooperators “
”, cooperators “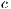 ” and defectors “
” and defectors “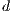 ”. A random group of
”. A random group of 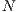 (
(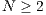 ) individuals are selected from the population. Cooperators and rewarders contribute
) individuals are selected from the population. Cooperators and rewarders contribute 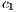 (
( ) to the game.
) to the game.
The obtained contribution is multiplied by 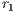 (
(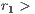 1) and then is divided among the players in two different ways depending on the type of game. If the amount is divided among all participants (
1) and then is divided among the players in two different ways depending on the type of game. If the amount is divided among all participants (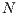 ), a portion of their contribution would return back to each player. This behavior is knows as weak altruism. On the other hand, in strong altruism type game, the amount is divided by
), a portion of their contribution would return back to each player. This behavior is knows as weak altruism. On the other hand, in strong altruism type game, the amount is divided by 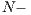 1 individuals. The CPGG with strong altruism is a social dilemma for any value of
1 individuals. The CPGG with strong altruism is a social dilemma for any value of 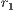 , with weak altruism is a social dilemma if
, with weak altruism is a social dilemma if  [14].
[14].
Rewarders contribute 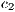 (
(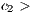 0) to a reward fund. The amount is multiplied by
0) to a reward fund. The amount is multiplied by 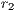 (
(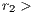 1) and distributed equally among all cooperators and rewarders. The reward system is; therefore, a social dilemma by itself if
1) and distributed equally among all cooperators and rewarders. The reward system is; therefore, a social dilemma by itself if 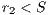 (where
(where 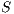 is the sum of cooperators and rewarders) [14].
is the sum of cooperators and rewarders) [14].
Payoffs are given by the sum of the CPGG payoff and the reward fund payoff:

where 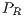 indicates the total payoff of rewarders, given by the sum of the payoff derived from the CPGG denoted by
indicates the total payoff of rewarders, given by the sum of the payoff derived from the CPGG denoted by 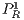 and the payoff from the reward fund denoted by
and the payoff from the reward fund denoted by 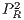 . Similar procedure is used for the total payoff of cooperators
. Similar procedure is used for the total payoff of cooperators 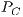 and defectors
and defectors 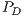 . For weak altruism CPGG payoffs are:
. For weak altruism CPGG payoffs are:
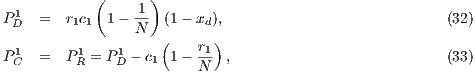

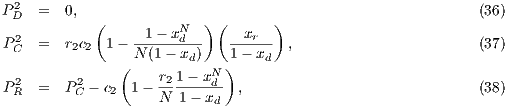
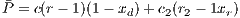 | (39) |
where 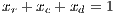 .
.
To maintain the cooperation in a CPGG with a reward system, the optimum group reward must be greater than the cost 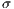 that contributors have to pay. For weak altruism
that contributors have to pay. For weak altruism 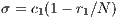 and for strong altruism
and for strong altruism 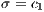 . The contribution to a PGG and reward funds can subsist even when second order exploiters (cooperators) dominate the rewarding system
. The contribution to a PGG and reward funds can subsist even when second order exploiters (cooperators) dominate the rewarding system 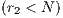 [14].
[14].
The strategies produce a cycle where rewarders are invaded by cooperators, cooperators by defectors and defectors are dominate by rewarders. In this model the defectors are responsible for maintaining the cycle, the same role played by loners in VPGG [14].
This outcome holds even if 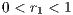 , as mentioned in [14]. That is the case of many global environmental and energy problems where cooperation gives little benefit on a short term and the dominant strategy is not to cooperate.
, as mentioned in [14]. That is the case of many global environmental and energy problems where cooperation gives little benefit on a short term and the dominant strategy is not to cooperate.
Again, the reward is a public good that can be exploited by cooperators who do not reward. To avoid this [14] proposed that cooperators are punished by reducing their reward in 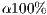
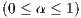 , assuming that
, assuming that 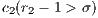 and
and 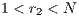 . Including second-order model sanctions causes the system to converge to a state with
. Including second-order model sanctions causes the system to converge to a state with 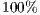 rewarders regardless of the initial condition [14].
rewarders regardless of the initial condition [14].
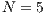 ,
, 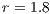 ,
, 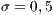 and (b)
and (b) 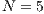 ,
, 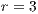 ,
, 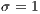 . (c) Model 2. VPGG without punishment. Parameters:
. (c) Model 2. VPGG without punishment. Parameters: 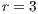 ,
, 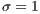 ,
, 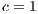 ,
, 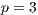 ,
, 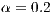 . (d) Model 4. VPGG with punishment. Parameters:
. (d) Model 4. VPGG with punishment. Parameters: 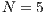 ,
, 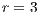 ,
, 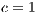 ,
, 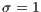 ,
, 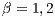 ,
, 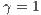
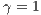
Model 6. The interaction between incentives provided by an institution (both positive and negative) and the abstention of the game as mechanisms to originate and stabilize cooperation was analyzed in [15]. Several variations were developed, they differ in how the contribution returns to the players or how the incentives are applied.
There are three strategies: cooperators “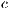 ”, defectors “
”, defectors “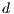 ” and loners “
” and loners “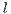 ”. In a large population, a sample group of
”. In a large population, a sample group of 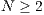 individuals, randomly selected, have the opportunity to participate in the game providing
individuals, randomly selected, have the opportunity to participate in the game providing 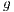 (
(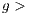 0). Each one of the
0). Each one of the 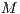
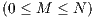 individuals who agree to participate decides whether or not to contribute
individuals who agree to participate decides whether or not to contribute 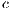 (
(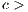 0) to the game; the collected amount is then multiplied by
0) to the game; the collected amount is then multiplied by 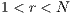 and divided by
and divided by 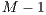 individuals (in the case of others-only variant). There must be at least two players to begin the game.
individuals (in the case of others-only variant). There must be at least two players to begin the game.
The total incentive defined by the sanctioning institution is 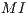 ( where
( where 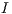 the incentive per capita ),
the incentive per capita ), 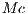 is the number of cooperators and
is the number of cooperators and 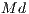 is the number of defectors. A cooperator would receive a reward equal to
is the number of defectors. A cooperator would receive a reward equal to 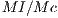 , if the incentive is positive, and a defector would decrease its payoff at
, if the incentive is positive, and a defector would decrease its payoff at 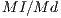 , if the incentive is negative) [15].
, if the incentive is negative) [15].
If there is no incentive, payoff strategies are defined by:
![( ) P oD = rc-xc--- g (1- xNl- 1), (40) 1- xl PoD - PoC = c(1- xNl -1), (41) ¯Po = (1 - xN -1)[(r- 1)cxc - (1- xl)g], (42) l](/img/revistas/cleiej/v17n2/2a07170x.png)
![r o P D = P D, (43) PrD - PrC = (PDo- PCo)- I[(1- xNl -1)+ xd(1- (1- xc)N-1)], (44) xc ¯Pr = P¯o + I[xc(1 - xNl-1+ xd(1- (1- xc)N-1))], (45)](/img/revistas/cleiej/v17n2/2a07171x.png)
![PpC = PoC, (46) p p o o N-1 xc N -1 PD - PC = (P D - P C)- I[(1 - xl )+ xd (1 - (1 - xd) )] (47) P¯p = ¯Po - I[x (1- xN- 1+ x (1 - (1 - x )N -1))] (48) d l c d](/img/revistas/cleiej/v17n2/2a07172x.png)
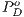 and
and 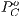 represent defectors and cooperators payoffs in a game without incentives, respectively. For the game with positive incentives, payoffs are given by
represent defectors and cooperators payoffs in a game without incentives, respectively. For the game with positive incentives, payoffs are given by 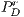 (defectors) and
(defectors) and 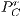 (cooperators); and for negative incentives, the payoff are
(cooperators); and for negative incentives, the payoff are 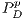 (defectors) and
(defectors) and 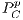 (cooperators).
(cooperators). 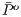 ,
, 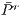 ,
, 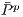 are average population payoff in a game without incentive, with positive and negative incentives, respectively.
are average population payoff in a game without incentive, with positive and negative incentives, respectively. In the absence of incentives, this model produces a cycle of strategies dominance (rock-scissors-paper type). Incentives are efficient in preventing the invasion of defectors in a group of cooperators but often not enough to convert a group of defectors into cooperators. Including the option to leave, the game improves the efficiency of incentives: it is less expensive to achieve cooperation in CPGG than it is in VPGG [15].
In VPGG with incentives, the results of the model depends on the amount and type of incentive. The reward is better to achieve the welfare of the group and to encourage desired behavior; however, it is more expensive. With a positive incentive, it is necessary to overcome the threshold 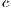 to reach
to reach 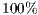 of cooperation. The negative incentive eventually achieves the same result only exceeding
of cooperation. The negative incentive eventually achieves the same result only exceeding 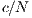 [15].
[15].
This model also develops some variations of the game [15]. In the self - returning variant, a portion of the contribution to the game returns to the contributor (as in weak altruism in Model 5). In this case, the dynamics of the system becomes more complex but the results are similar.
Another variant would be that players must pay a fee aimed exclusively to provide incentives (user pays variant). For this variant, results do not differ very much unless the fee is very high. As an extension of the same variant, [15] studied the return of the fee to the population if there were no defectors. In this case small negative incentives are sufficient to maximize social welfare [15].
Within the first part of this section we show the results obtained from the models, which are compared and systematized in Table 1 according to their characteristics. In a second point, the models are applied in a real study case with real data. The models were implemented in Matlab©, using the formulation described in the previous Sections.
In Model 1 (a VPGG with three strategies: cooperators, defectors and loners), a rock-scissors-paper loop is established [10]. When in the population exists a large percentage of cooperators, defectors will invade. It occurs because defectors receive a higher payoff by participating in the game without any contribution. When the defector population grows, their payoff will decrease up to it becomes lower than the loners’ payoff. At this moment, the loners would invade the population of defectors and this strategy would increase its participation. When the loners have the supremacy within the total population, the number of players decreases and the payoff of cooperators increases up to it becomes better than the loners’ payoff. Finally, under these conditions, the cooperators would invade again the population; increasing the defectors’ payoff up to it is larger than the cooperator ones, closing the aforementioned loop.
The results vary with the value of 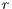 [10], which is the amount by which the contribution
[10], which is the amount by which the contribution 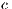 of cooperators is multiplied. Following [10]; it is possible to note that if
of cooperators is multiplied. Following [10]; it is possible to note that if 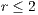 (Fig. 1(a)), the system exhibits peaks of cooperation with long periods of loner prevalence, whereas if
(Fig. 1(a)), the system exhibits peaks of cooperation with long periods of loner prevalence, whereas if 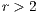 , an equilibrium point appears surrounded by closed orbits (see Fig. 1(b)).
, an equilibrium point appears surrounded by closed orbits (see Fig. 1(b)).
Model 2 introduces a punisher strategy. In the results is observed (Fig. 1(c)) that the cyclic dominance of the three strategies still remains, but a region where the population tends to the state 100% of punishers appears [11].
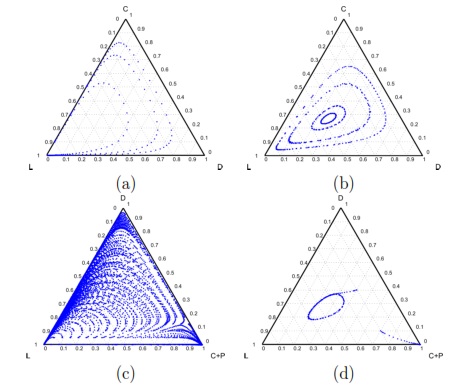
For the Model 4, we adopt the following settings 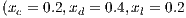 and
and 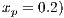 and
and 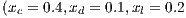 and
and 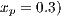 . It can be seen that in an infinite population, the result depends on the initial conditions [13] (see Fig. 1(d)). Under these conditions, it can be generated either a neutral mixture of cooperators and punishers where both receive the same payoff (in the absence of defectors to whom punish) or the punishers can disappear and reappear the cyclic dominance among strategies [13].
. It can be seen that in an infinite population, the result depends on the initial conditions [13] (see Fig. 1(d)). Under these conditions, it can be generated either a neutral mixture of cooperators and punishers where both receive the same payoff (in the absence of defectors to whom punish) or the punishers can disappear and reappear the cyclic dominance among strategies [13].
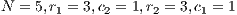 and (b)
and (b) 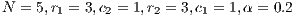 . C = Cooperators, R = Rewarders and D = Defectors
. C = Cooperators, R = Rewarders and D = Defectors
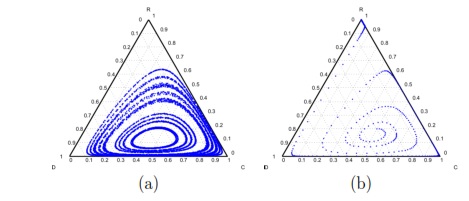
In Model 5, the game is compulsory and the cooperators are rewarded. The output of this model is a rock-scissors-paper cyclic dominance among cooperators, defectors and rewarders [14] (see Fig. 2(a)).
If those that do not reward cooperators (second-order exploiters) are punished by reducing their payoff, the system would be able to converge to a state with 100% rewarders regardless of the initial conditions [14] (see Fig. 2(b))
 ,
, 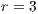 ,
, 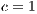 ,
, 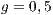 ,
, 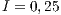 , (b)
, (b) 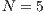 ,
, 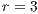 ,
, 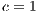 ,
, 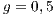 ,
, 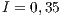 , (c and d)
, (c and d) 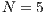 ,
, 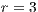 ,
, 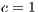 ,
, 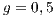 ,
, 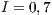 . C = Cooperators, L =Loners and D = Defectors
. C = Cooperators, L =Loners and D = Defectors
In Model 6, the game is voluntary (VPGG) with incentives. The results depend on the amount and kind of incentive. If the incentive is less than 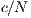 , it does not take effect but, if it is greater than
, it does not take effect but, if it is greater than 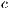 , then the cooperation is always achieved. The effect achieved with intermediate values varies with the kind of incentive [15].
, then the cooperation is always achieved. The effect achieved with intermediate values varies with the kind of incentive [15].
As in [15], in Figs. 3(a) and (b), we can see how the results change substantially, if the amount of the incentive is varied but it is used the same kind of incentive. In this case, the reward is incremented, and as response of this perturbation, the percentage of cooperators would increase. In Figs. 3(c) and (d), the amount of incentive is fixed. The results correspond to the two types of incentives (reward and punishment). It can be seen that the reward produces the coexistence of cooperators and defectors which does not happen with punishment where a state of cooperation is eventually obtained [15].
Table 1 presents a summary of the studied models pointing out their main characteristics: the type of game, existing strategies, the type of incentive and how it is applied, as well as the conditions needed to run the model.
At the literature it is observed the utilization of a combination of an abstention mechanism with incentives to sustain and improve cooperation. Abstention facilitates the establishment of cooperation to prevent that the defectors can totally dominate the population [10]. Once cooperation is established, incentives serve to prevent the invasion of defectors [15]. However, it is not always possible to abandon the game. Compulsory games (CPGG) can be used in these cases [14].
It is noted that the way to implement punishment was evolved over the time. Models using peer-punishment/rewarding have evolved to pool-punishment/rewarding. Hence, the punishment or reward strategies disappear and become a contribution fee to the game. This contribution is used later to apply sanctions or rewards.
Therefore, the system has evolved from one where the society members punish the exploiters to a model where there is an institution that deals with punishment.
As a practical study case we use three of the described models in two Sanitation Boards (SBs). The SBs are civil associations that provide drinking water and sanitation in rural and urban communities with populations up to 10,000 inhabitants [32]. According to surveys conducted by the General Office of Statistics, Surveys and Censuses of Paraguay (DGEEC) in the Yearbook 2010, the SBs provide drinking water to 27.1% of the population in Paraguay [33].
The SBs often present problems of cooperation, [34] mentions the lack of payment as one of the main problems that affect the sustainability of many boards over the time.
Defaulting in SBs represents a social dilemma or social trap; those who do not pay (defectors) are short-term beneficiary by saving the payment but receiving the service anyway. In this situation, in long-term, the number of defaulting users increases and the payers (cooperators) are not enough to sustain the SBs. Hence, the whole community -either cooperators or defectors- suffers.
The sustainability problem of a water supply project due to the defaulting of their users is formulated according to the game theory approach in [35]. This paper analyzed social projects in rural communities in South Africa and notes that many of them fail because they cannot raise enough funds for the operation and maintenance of water supply service.
Conversely to [35] which used classical game theory to analyze the situation, in this paper we use Evolutionary Game Theory. Evolutionary Game Theory models the dynamics of the game and analyzes the interaction among the different strategies. If the real data of a SB is used, it would be possible to predict the future behavior according to a given model. With this information, managers of SBs can develop policies tending to prevent unfavorable outcomes and to encourage the desired behavior.
The first SB to analyze is one placed in San Juan Nepomuceno (SJN). The data necessary to apply the models are extracted from [36]. This SB has 1650 users (connections). An average of 1028 users pay the service every month. Therefore, the cooperator percentage is equal to 62% and the defector percentage is 38%.
The second SB analyzed is placed in the town of Villa Ygatimi (VY). According to [37], defaulting users constitute 50% of the total.
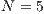 ,
, 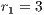 ,
, 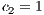 ,
, 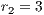 ,
, 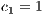 and (b)
and (b) 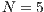 ,
, 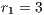 ,
, 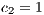 ,
, 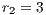 ,
, 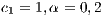 . Initial conditions: (SJN)
. Initial conditions: (SJN) 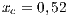 ;
; 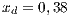 ;
; 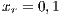 and (VY)
and (VY) 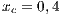 ;
; 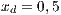 ;
; 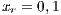 . C = Cooperators, R = Rewarders and D = Defectors
. C = Cooperators, R = Rewarders and D = Defectors .
3.2.1 Compulsory public good games (CPGG)
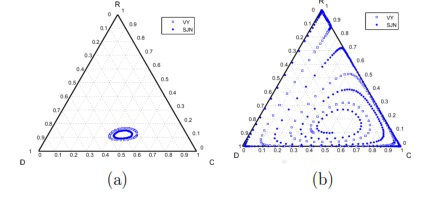
If the SB is the only water supply alternative of a given community, then the game is compulsory, i.e. the player cannot avoid the game. In this case, Model 5 is used. This model includes three strategies, cooperators, defectors and rewarders. We assume that 10% of the cooperators decide to implement a system of rewards and become rewarders, then the population of San Juan Nepomuceno shall consist of 52 % of cooperators, 38% of defectors and 10% rewarders. Likewise, Villa Ygatimi population would have 40% cooperators, 50% defectors and 10% rewarders.
Figs. 4 (a) and (b) show the result of the Model 5 without punishment and with second order punishment, respectively. It is possible to observe the dominance loop, where cooperation strategy does not reach 100% but it does not completely disappear (Fig. 4a). The frequency of each of the three strategies dynamically changes and after a given time returns to its original set of values when the loop is closed.
From the SBs point of view, this means that the project will have upward and downward movements with good times when most users are cooperators or rewarders and bad times when most users are defectors. The SB Villa Ygatimi will have upward and downward movements more pronounced than the SB of San Juan Nepomuceno. Essentially both SBs have qualitatively similar behavior.
Imposing a punishment to those users who do not reward the cooperators by extracting 20% of their income 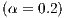 , then we obtain, over the time, a population composed entirely of rewarders, as it is shown in Fig. 4(b). In a SB, this would mean that eventually there would not be defectors in the community and that each user would provide to both the project and the reward fund (100 % rewarders). However, this result would not be achieved immediately.
, then we obtain, over the time, a population composed entirely of rewarders, as it is shown in Fig. 4(b). In a SB, this would mean that eventually there would not be defectors in the community and that each user would provide to both the project and the reward fund (100 % rewarders). However, this result would not be achieved immediately.
Hence, the SB will go through stages of very good performance when the majority of the population are rewarders. At this time, the percentage of cooperators would begin to increase overtaking rewarders. As cooperation still exists, the SB will not feel much change, but a community composed mainly of cooperators, might be invaded by defectors.
Increasing the percentage of defectors, the SB will struggle to survive. After some time; however, the number of rewarders increase in the population, exceeding the percentage continuously, the same would happen later with cooperators and defectors (see Fig. 4(b) ).
Therefore, the SB will pass through good and bad times. Good times even better and better and bad times increasingly difficult to overcome, that would threaten the survival of the board.
In the case of Villa Ygatimi after good and bad times, the population is -for a given time- composed just by cooperators and rewarders with no defectors. Cooperators gradually change their strategy and eventually the population will be composed only by rewarders (point R at Fig. 4 (b)).
The SB of San Juan Nepomuceno; practically disappears before reaching the point R. Defectors constitute almost the entire population before being gradually overtaken by rewarders to increase in the group up to 100%.
3.2.2 Voluntary public good games (VPGG)
If it is assumed that users can obtain water from an alternative source, then the game is voluntary. In order to analyze this scenario, we select two models.
Model 1, which does not use incentives and Model 6, where the policy-maker can use incentives. In addition, this model allows choosing between reward or punishment (Model 6).
Both models have three strategies: cooperators, defectors and loners. As in the previous case, in order to consider the three strategies it has been chosen that 10% of the cooperators become loners (abandon the project) due to a high defaulting group. Therefore, for the models, we consider an initial stage consisting of 40% cooperators, 50% defectors and 10% loners (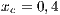 ;
; 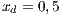 and
and 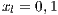 ) for Villa Ygamiti, while San Juan Nepomuceno is composed of 52% cooperators, 38% defectors and 10% loners (
) for Villa Ygamiti, while San Juan Nepomuceno is composed of 52% cooperators, 38% defectors and 10% loners (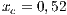 ;
; 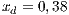 and
and 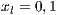 ).
).
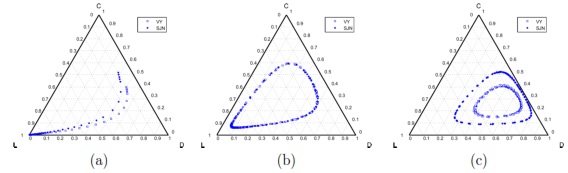
 ,
,  , (a)
, (a)  , (b)
, (b) 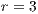 and (c)
and (c) 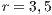 . Initial conditions: (SJN)
. Initial conditions: (SJN) 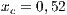 ;
; 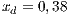 ;
; 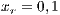 and (VY)
and (VY) 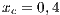 ;
; 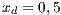 ;
; 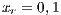
Model 1. With this model the strategies generate a cyclic dominance of strategies similar to that observed in Model 5, but with different strategies. When the SB is composed mainly by cooperators, it works smoothly; however, it would be susceptible to an increment of defectors.
When the number of defectors is increased, the SB has a lower income and it is difficult to keep running. Under these circumstances, users choose to leave the project (become loners). The SB is reduced to a very few users, and may even be shutdown.
If the user group becomes very small and is mainly composed by cooperators the SB would be able to recover, since the cooperator benefit is greater than the loner ones. Even in the case where the SB disappears, it is possible that a group of cooperators could be able to reactivate the project, due to the necessity to have water supply service in the community. In such cases, the cooperation will increase again within the population closing the dynamic loop.
As mentioned above, in Model 1 the results depend on the value of 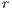 , the value by which the total contribution of the cooperators is amplified. Therefore, increasing
, the value by which the total contribution of the cooperators is amplified. Therefore, increasing 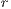 the benefit received by each of the participants is raised. In fact, from this point of view, the value of
the benefit received by each of the participants is raised. In fact, from this point of view, the value of 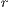 can be considered as a measure of the efficient management of the resources of the board.
can be considered as a measure of the efficient management of the resources of the board.
The most obvious effect of increasing 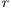 is the decrement in the loner percentage (see Figs. 5 (a), (b) and (c)). This may be explained presupposing that a board of efficient sanitation is attractive for those who initially chose not to participate in the project obtaining the water from an independen supply. Comparing the result of Figs. 5 (a), (b) and (c), when the loners enter into the project as cooperators, we conjecture that some old cooperators decide to stop contributing and become defectors. By this reason, it is possible to explain the decrease of cooperators and increment of defectors.
is the decrement in the loner percentage (see Figs. 5 (a), (b) and (c)). This may be explained presupposing that a board of efficient sanitation is attractive for those who initially chose not to participate in the project obtaining the water from an independen supply. Comparing the result of Figs. 5 (a), (b) and (c), when the loners enter into the project as cooperators, we conjecture that some old cooperators decide to stop contributing and become defectors. By this reason, it is possible to explain the decrease of cooperators and increment of defectors.
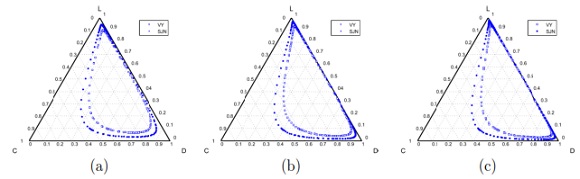
Model 6. In the absence of incentives, this model produces the dominance of strategies of the type rock-scissors-paper cycle [15]. Fig. 6 shows the results when varying the contribution 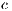 (cost of service) of the cooperator in a game without any incentives. Notice that when the cost of the service is increased, the cooperation is not improved. In addition, the defaulting problem is not solved because the users who are paying for the service have to pay even more, while defectors are not affected by this situation. As a consequence, this policy discourage cooperation.
(cost of service) of the cooperator in a game without any incentives. Notice that when the cost of the service is increased, the cooperation is not improved. In addition, the defaulting problem is not solved because the users who are paying for the service have to pay even more, while defectors are not affected by this situation. As a consequence, this policy discourage cooperation.
At Figs. 6 (b) and (c) can also be observed that the decrement in the cooperation (when 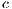 is increased) is closely related with the increment of the defectors and loners percentage. Even for
is increased) is closely related with the increment of the defectors and loners percentage. Even for 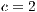 , the cooperation disappears at a given time (Fig. 6(c)) and then it appears again.
, the cooperation disappears at a given time (Fig. 6(c)) and then it appears again.
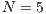 ,
, 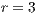 ,
, 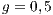 ,
, 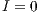 , (a)
, (a) 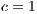 , (b)
, (b) 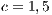 and (c)
and (c) 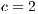 . Initial conditions: (SJN)
. Initial conditions: (SJN) 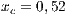 ;
; 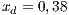 ;
; 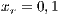 and (VY)
and (VY) 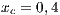 ;
; 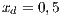 ;
; 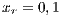
By adding incentives, the final results changes. Model 6 presents different alternative for analyzing PGGs. We adopt the so-called “self-returning” since within this approach each player receives back part of their contribution, due to the fact that the total profit is divided among all users. As mentioned in [15], when the incentive is very small (less than 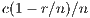 ), the effect is imperceptible and when it is very large (greater than
), the effect is imperceptible and when it is very large (greater than 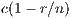 ), the result is always full cooperation. Intermediate values produce different results depending on the type of incentive.
), the result is always full cooperation. Intermediate values produce different results depending on the type of incentive.
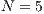 ,
, 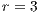 ,
, 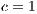 ,
, 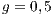 , (a) and (c)
, (a) and (c) 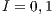 , (b) and (d)
, (b) and (d) 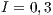 . Initial conditions: (SJN)
. Initial conditions: (SJN) 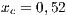 ;
; 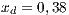 ;
; 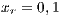 and (VY)
and (VY) 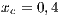 ;
; 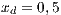 ;
; 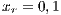
.
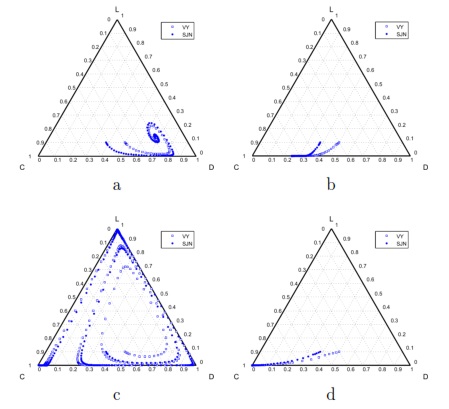
According to this model, if within the community the users who pay on time the water service (cooperators) are rewarded then the cooperation is improved.
For a small incentive (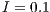 ), the result consist in the coexistence of three strategies: cooperators, defectors and loners; but with a clear majority of defectors (between 60% and 70% of the total population). This SB would be able to endure over the time (Fig. 7 (a)), even though the total population is not going to be involved and service would be poor due to the high default rate.
), the result consist in the coexistence of three strategies: cooperators, defectors and loners; but with a clear majority of defectors (between 60% and 70% of the total population). This SB would be able to endure over the time (Fig. 7 (a)), even though the total population is not going to be involved and service would be poor due to the high default rate.
If the reward is increased to 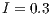 , loners disappear (the full population participate in the project) but still maintaining the coexistence of cooperators and defectors. Nevertheless, the percentage of cooperators increase significantly, by reaching more than 70% of the population (Fig. 7 (b)).
, loners disappear (the full population participate in the project) but still maintaining the coexistence of cooperators and defectors. Nevertheless, the percentage of cooperators increase significantly, by reaching more than 70% of the population (Fig. 7 (b)).
Using negative incentives and punish the defaulters (defectors), the community eventually reaches 100% cooperation.
If 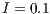 , the SB goes good times (getting better) and difficult times (getting worse). At the end it arrives to a group composed exclusively of cooperators. Although the final result is satisfactory, the entire process can be a hazard to the SB survival (Fig. 7 (c)).
, the SB goes good times (getting better) and difficult times (getting worse). At the end it arrives to a group composed exclusively of cooperators. Although the final result is satisfactory, the entire process can be a hazard to the SB survival (Fig. 7 (c)).
With 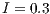 , fluctuations are not observed, the percentage of cooperators increases gradually up to 100% of the population, which means that the SB improves gradually (Fig. 7 (d)).
, fluctuations are not observed, the percentage of cooperators increases gradually up to 100% of the population, which means that the SB improves gradually (Fig. 7 (d)).
Under both positive and negative incentives, we can see that for this model, both SB behave very similarly.
In this work, we reviewed several models introduced to analyze the evolution of cooperation. We classified them in accordance to their main characteristics in order to select those more appropriate to a specific real case.
The sanitation board - SB - is presented as a real practical problem; this type of initiative has often problems of cooperation. Two boards with real data are analyzed using three selected models: Model 1, Model 5 and Model 6.
The cycles are a common result. They may appear in every model under certain circumstances. In a SB, it implies that the project will go through different stages of more or less success depending on the dominant strategy at that time of the cycle.
It can be observed how different variants in Model 5 produce radically different solutions. In fact, the inclusion of negative incentive for cooperators implies the difference between a SB that manages to sustain over the time even with low cooperation or a SB that eventually reaches 100% of cooperation.
In this case, although it is possible to obtain a group composed exclusively by rewarders, it is important to consider that the SB must overcome several difficult stages with a percentage of ever higher nonpayment to achieve cooperation. Therefore, the SB has a great potential in real life to disappear before eventually obtain full cooperation.
The abstention mechanism by itself without the need for any incentive encourages the continuation of the SB over the time, as can be seen in Model 1. Successive cycles are presented with predomination of cooperation and defection in the group. Depending on the amplitude of the cycles, the quality of service and operation of the SB would be more or less affected. Eventually, there are situations where cooperation is very small or even does not exist, generating that most of the members of the community or even all of them abandon the project. This situation is not permanent, considering the importance of the provision of drinking water some individuals will return back to the SB, restoring cooperation.
In Model 6, it can be noticed that incentives improve the cooperation that exists within the group. The reward produces increased cooperation, but keeps a percentage of defectors in the population. The punishment forces the cooperation of all. While the ideal would be to achieve the cooperation of the entire group, it is necessary to consider in a real situation as in the case of SB, the process by which the community must pass to reach it is also very important.
By applying a reward, as the incentive increases gradually, also the cooperation within the community increases. With punishment, if the value is small, SB could go through successive cycles of defection and cooperation, which are becoming more pronounced and could even jeopardize the existence of the board instead of achieving the desired goal of cooperation.
It has not been done yet the follow-up analysis needed to compare the simulation results with the actual situation of the SB. However, if we consider the news about SB that appear in the media dealing mostly from the openings of new SBs and the interventions of SBs with serious nonpayment problems, we have reasonable assurance that phenomena like cycle of strategies that appear on models also occurs in reality.
While each SB should be studied individually, some general policies can be obtained from the results of the models, which are mentioned next. If possible keep a voluntary game, thus maintaining cooperation in time.
If the goal is to reinforce cooperative behaviour such as timely payment of water fees, rewards should be used. If instead, what is sought is the full cooperation regardless of the process, punishment should be used. In both cases the incentive must be at least moderate for fast and noticeable results. If the reward is very low, few persons would modify their behaviour and improvement would not be apparent in the community. If instead the punishment is very low, SB will go through several cycles of good and bad times before reaching cooperation.
It should also be noted that increasing the cost of the service in order to raise the money needed to keep the board running may have an unexpected result of discourage the cooperators who are going to take into account the increment of the cost.
[1] J. M. Smith and G. R. Price, “The Logic of Animal Contest,” Nature, vol. 246, no. 2, pp. 15–18, 1973.
[2] J. Von Neumann and O. Morgenstern, Theory of games and economic behavior, ser. Science: Economics. Princeton University Press, 1953. [Online]. Available: http://books.google.com.py/books?id=gGYGAQAAIAAJ
[3] C. Darwin, On the Origin of the Species by Means of Natural Selection: Or, The Preservation of Favoured Races in the Struggle for Life. John Murray, 1859. [Online]. Available: http://books.google.com.py/books?id=jTZbAAAAQAAJ
[4] J. M. Smith, “Evolutionary game theory,” Physica D: Nonlinear Phenomena, vol. 22, no. 1-3, pp. 43–49, Oct. 1986. [Online]. Available: http://www.sciencedirect.com/science/article/pii/0167278986902320
[5] J. Hofbauer and K. Sigmund, “Evolutionary game dynamics,” Society, vol. 40, no. 4, pp. 479–519, 2003.
[6] P. D. Taylor and L. B. Jonker, “Evolutionary stable strategies and game dynamics,” Mathematical Biosciences, vol. 40, no. 1-2, pp. 145–156, Jul. 1978. [Online]. Available: http://linkinghub.elsevier.com/retrieve/pii/0025556478900779
[7] R. L. . Trivers, “The Evolution of Reciprocal Altruism Published by : The University of Chicago Press Stable URL :,” The Quarterly Review of Biology, vol. 46, no. 1, pp. 35–57, 1971. [Online]. Available: http://www.jstor.org/stable/2822435
[8] S. Kuhn, “Prisonerś dilemma,” in The Stanford Encyclopedia of Philosophy, spring 2009 ed., E. N. Zalta, Ed., 2009.
[9] R. Axelrod and W. Hamilton, “The evolution of cooperation,” Science, vol. 211, no. 27, pp. 1390 – 1396, 1981. [Online]. Available: http://wuos.org/content/211/4489/1390.short
[10] C. Hauert, S. De Monte, J. Hofbauer, and K. Sigmund, “Volunteering as Red Queen mechanism for cooperation in public goods games.” Science (New York, N.Y.), vol. 296, no. 5570, pp. 1129–32, May 2002. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/12004134
[11] J. H. Fowler, “Altruistic punishment and the origin of cooperation.” Proceedings of the National Academy of Sciences of the United States of America, vol. 102, no. 19, pp. 7047–9, May 2005. [Online]. Available: http://tinyurl.com/9uq8tql
[12] H. Brandt, C. Hauert, and K. Sigmund, “Punishing and abstaining for public goods.” Proceedings of the National Academy of Sciences of the United States of America, vol. 103, no. 2, pp. 495–7, Jan. 2006. [Online]. Available: http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3020126
[13] C. Hauert, A. Traulsen, H. Brandt, M. A. Nowak, and K. Sigmund, “Public Goods With Punishment and Abstaining in Finite and Infinite Populations,” Biological Theory, vol. 3, no. 2, pp. 114–122, 2008.
[14] T. Sasaki and T. Unemi, “Replicator dynamics in public goods games with reward funds.” Journal of theoretical biology, vol. 287, pp. 109–14, Oct. 2011. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/21824483
[15] T. Sasaki, A. Brännström, U. Dieckmann, and K. Sigmund, “The take-it-or-leave-it option allows small penalties to overcome social dilemmas.” Proceedings of the National Academy of Sciences of the United States of America, vol. 109, no. 4, pp. 1165–9, Jan. 2012. [Online]. Available: http://tinyurl.com/99dfe2n
[16] W. D. Hamilton, “The genetical evolution of social behaviour. I.” Journal of theoretical biology, vol. 7, no. 1, pp. 1–16, Jul. 1964. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/5875341
[17] M. A. Nowak and K. Sigmund, “Evolution of indirect reciprocity by image scoring.” Nature, vol. 393, no. 6685, pp. 573–7, Jun. 1998. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/9634232
[18] M. Nowak and R. May, “Evolutionary games and spatial chaos,” Nature, vol. 359, 1992. [Online]. Available: http://tinyurl.com/8sahrcf
[19] G. Hardin, “The Tragedy of the Commons,” Science, vol. 162, pp. 1243–1248, 1968. [Online]. Available: http://www.tandfonline.com/doi/abs/10.1080/19390450903037302
[20] ——, “Extensions of The Tragedy of the Commons ,” no. May, pp. 1–2, 1998.
[21] E. Fehr and S. Gächter, “Altruistic punishment in humans.” Nature, vol. 415, no. 6868, pp. 137–40, Jan. 2002. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/11805825
[22] K. Sigmund, H. De Silva, A. Traulsen, and C. Hauert, “Social learning promotes institutions for governing the commons.” Nature, vol. 466, no. 7308, pp. 861–3, Aug. 2010. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/20631710
[23] K. Sigmund, C. Hauert, A. Traulsen, and H. Silva, “Social Control and the Social Contract: The Emergence of Sanctioning Systems for Collective Action,” Dynamic Games and Applications, vol. 1, no. 1, pp. 149–171, Oct. 2010. [Online]. Available: http://www.springerlink.com/index/10.1007/s13235-010-0001-4
[24] C. Hilbe and K. Sigmund, “Incentives and opportunism: from the carrot to the stick.” Proceedings. Biological sciences / The Royal Society, vol. 277, no. 1693, pp. 2427–33, Aug. 2010. [Online]. Available: http://tinyurl.com/8j9ha8e
[25] D. Semmann, H.-J. Krambeck, and M. Milinski, “Volunteering leads to rock paper scissors dynamics in a public goods game,” Nature, vol. 425, no. September, 2003.
[26] M. A. Nowak, “Five Rules for the Evolution of Cooperation,” Science, vol. 314, no. December, 2006.
[27] H. Curtis, Biologia, 4th ed. Worth Publishers, 1987.
[28] E. Fehr and U. Fischbacher, “Social norms and human cooperation.” Trends in cognitive sciences, vol. 8, no. 4, pp. 185–90, Apr. 2004. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/15050515
[29] R. Dawes, “Social dilemmas,” Annual review of psychology, 1980. [Online]. Available: http://www.annualreviews.org/doi/abs/10.1146/annurev.ps.31.020180.001125
[30] C. Hauert, S. D. Monte, J. Hofbauer, and K. Sigmund, “Replicator Dynamics for Optional Public Good Games,” Journal of theoretical biology Theoretical Biology, vol. 218, no. 2, pp. 187–194, 2002.
[31] C. Taylor, D. Fudenberg, A. Sasaki, and M. a. Nowak, “Evolutionary game dynamics in finite populations.” Bulletin of mathematical biology, vol. 66, no. 6, pp. 1621–44, Nov. 2004. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/15522348
[32] OPS, Actualización del análisis sectorial de agua potable y saneamiento de Paraguay, 2010.
[33] DGEEC, “Anuario Estadístico del Paraguay 2010,” in Anuario Estadístico del Paraguay 2010. Fernando de la Mora: DGEEC, 2012, ch. 2. [Online]. Available: http://www.dgeec.gov.py/Publicaciones/Biblioteca/Anuario2010/cap 02 2010.pdf
[34] PNUD, “Experiencias ciudadanas innovadores: juntas de saneamiento y farmacias sociales en el Paraguay,” Tech. Rep., 2008.
[35] M. Breier and M. Visser, “The Free Rider Problem in Community-Based Rural Water Supply: A Game Theoretic Analysis,” no. 06, 2006. [Online]. Available: http://ideas.repec.org/p/ldr/wpaper/5.html
[36] ABC, “Recomiendan actualizar tarifa de provisión de agua en Caazapá,” Jul. 2012. [Online]. Available: http://www.abc.com.py/edicion-impresa/suplementos/economico/recomiendan-actualizar-tarifa-de-provision-de-agua-en-caazapa-420652.html
[37] J. Martínez, R. Giménez, E. Garay, I. S. de Sanabria, S. Alvarenga Giménez, and E. Gonzalez Caballero, “Propuesta Plan de Desarrollo Sustentable y ordenamiento territorial del municipio de Villa Ygatimi Departamento de Canindeyú Septiembre - 2012,” Tech. Rep., 2012.