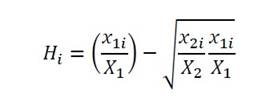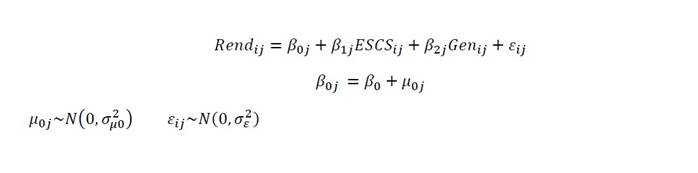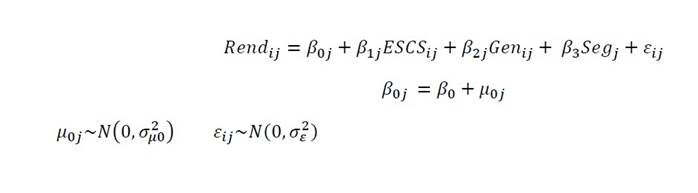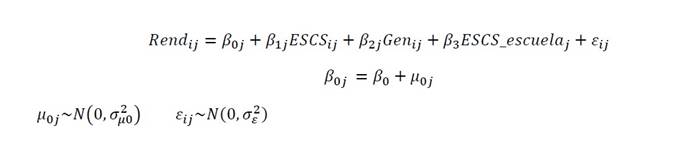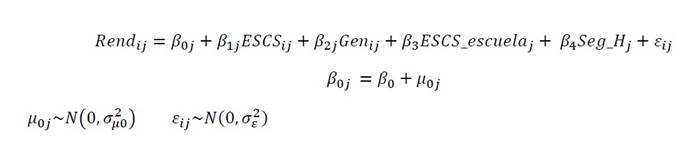Introducción

Será imposible alcanzar el Objetivo de Desarrollo Sostenible 4: “Garantizar una educación inclusiva, equitativa y de calidad y promover oportunidades de aprendizaje durante toda la vida para todos” con las altas tasas de segregación escolar que tienen la mayoría de los sistemas educativos de América Latina. Uruguay, a pesar de su situación privilegiada frente a otros países de la región, no escapa a esta problemática. Efectivamente, recientes estudios (^{Ferrando et al., 2020}; ^{Murillo, Duk y Martínez-Garrido, 2018}; ^{Murillo y Graña, 2020}; ^{Murillo y Martínez-Garrido, 2017a}) han mostrado que, aunque la segregación escolar de Uruguay es menor para los estudiantes con familias de menor nivel socioeconómico, ésta es muy alta para los estudiantes de familias con más recursos.

Entendemos por segregación escolar la desigual distribución de los estudiantes en las escuelas en función de sus características personales o sociales o de su condición, en este caso el nivel socioeconómico de las familias de los estudiantes. Para cada escuela, esta definición se operativiza como la distancia entre la media geométrica de las participaciones de estudiantes de distinto nivel socioeconómico en ausencia de segregación y la media geométrica de las participaciones reales (^{Murillo, 2016}).

La segregación escolar está directamente relacionada con el abandono escolar, la repetición, el bajo rendimiento y las escasas expectativas académicas de los estudiantes, lo que impide una verdadera igualdad de oportunidades o de posiciones, y contribuye de manera fundamental a la construcción de una sociedad desigual, excluyente e injusta (^{Elias y Daza, 2019}; ^{Krüger, 2018}; ^{Murillo y Carrillo, 2021}; ^{Owens, 2018}). Pese a los más de 65 años de investigación sobre esta temática, todavía existen muchos aspectos que dificultan y complejizan la comprensión de esta problemática. Así, por mencionar algunos, aún no hay consenso acerca de la definición del término ni sobre la forma de estimar su magnitud. Tampoco hay acuerdo sobre las variables usadas para medir los distintos tipos de segregación o sobre la conformación de los grupos minoritarios. Pero, además de las cuestiones metodológicas, todavía existen multitud de aspectos sobre la segregación escolar de las que no se tiene toda la información necesaria, especialmente las causas, las consecuencias y, lo que es más importante, las medidas necesarias para luchar contra este desafío. De esta forma, no se podrán tomar medidas que contribuyan a acabar con esta grave problemática sino se profundiza en su conocimiento.

Así, se disponen aún de limitadas evidencias sobre el impacto que tiene la segregación en los estudiantes. En cambio, se dispone de claras evidencias sobre la incidencia de las características de los estudiantes, incluida la incidencia del nivel socioeconómico, sobre el rendimiento académico de compañeros, el llamado “efecto pares” -peer effect en inglés- (por ejemplo: ^{Bäckström, 2021}; ^{Burdick-Will, 2018}; ^{Chesters y Daly, 2017}; ^{Lugo, 2011}; ^{Krüger, 2020}; ^{Paloyo, 2020}). Sin embargo, el impacto de la segregación escolar, aunque está relacionado, no es lo mismo que el efecto compañeros. Y el estudio con datos de un sistema educativo con una alta segregación escolar de los estudiantes de familias con más recursos socioeconómicos, es innovador.

Esta investigación busca determinar, en primer lugar, la incidencia de la segregación escolar sobre el desempeño de los estudiantes de Educación Primaria de Uruguay. En segundo término, dada la relación entre la segregación y el efecto de los pares, se pretende determinar la incidencia de la segregación escolar en el rendimiento controlando el efecto pares. La elección de Uruguay viene determinada por sus especiales características, un país con una segregación escolar para estudiantes de familias más vulnerables baja, en comparación con los países de su entorno, y muy alta para estudiantes con familias de más recursos. Para ello, se realiza un análisis multinivel en dos niveles (escuela y estudiante) con datos de la evaluación nacional Aristas 2017.

Marco Teórico

El imprescindible punto de partida que abrió los ojos a la comunidad investigadora -y a toda la sociedad- acerca de la importancia del contexto y de los compañeros del estudiante sobre su aprendizaje fue el Informe ^{Coleman (Coleman et al., 1966}). Dicho estudio destacó la influencia del contexto socioeconómico y de la composición estudiantil de una escuela o un aula en los resultados escolares, por encima de otros factores escolares como las instalaciones, el plan de estudios, la metodología del docente o el gasto por alumno.

Desde entonces se han multiplicado las investigaciones que buscan determinar cómo influye el nivel socioeconómico de los compañeros en el logro académico del estudiante (por ejemplo: ^{Bartholo y Costa, 2016}; ^{Dumay y Dupriez, 2008}; ^{Krüger, 2020}; ^{Lugo, 2011}; ^{Mickelson, 2018}; ^{Van Ewijk y Sleegers, 2010}; entre otros). El efecto pares, en sentido general, hace referencia a la interdependencia en el comportamiento de los diferentes miembros de un grupo. En el ámbito escolar se centra en la asociación entre las medidas agregadas o promedio de las características demográficas de los estudiantes, especialmente el promedio del nivel socioeconómico de los estudiantes del aula o la escuela, y los resultados educativos (^{Dumay y Dupriez, 2008}; ^{Palardy, 2013}). En otras palabras, se refiere a la incidencia del promedio socioeconómico sobre el rendimiento de compañeros que asisten a la misma escuela.

La investigación ha encontrado claras evidencias del efecto pares en educación, tanto en relación con los logros académicos de los estudiantes como los no académicos. Sin embargo, para muchos investigadores e investigadoras la causalidad del efecto pares sobre los logros académicos es todavía una materia pendiente, enfrentándose a algunas limitaciones conceptuales y problemáticas relacionadas, entre otras cosas, con la calidad de los datos (por ejemplo: Bellei, 2013; ^{Lugo, 2011}; ^{Sacerdote, 2014}; ^{Sirin, 2005}; ^{Van Ewik y Sleegers, 2010}).

Quizá el estudio clave sobre este tema es el trabajo de Van Ewik y Sleegers (²⁰¹⁰). Estos autores realizan un metaanálisis de los hallazgos de estudios previos con la intención de comprender por qué investigaciones semejantes han encontrado alternativamente diferentes impactos en el rendimiento de los estudiantes. Encuentran que existen tres elementos clave que son usados de forma diferente en los estudios analizados y que hacen que se hallen resultados tan dispares: la muestra, el modelo de estimación y la variable criterio de nivel socioeconómico. Así, por ejemplo, encuentran que los estudios que utilizan variables dicotómicas para controlar el nivel socioeconómico de los estudiantes encuentran un impacto mucho menor sobre el efecto de los pares en comparación con los estudios que utilizan varias dimensiones para estimar el nivel socioeconómico de los estudiantes.

El modelo de estimación empleado es un tema controvertido a la hora de estimar el efecto de los pares en el rendimiento académico. ^{Lugo (2011}), por ejemplo, destaca que el problema se encuentra en el uso de un modelo lineal que parte del supuesto de que los efectos de los pares son homogéneos, es decir que afectan a todos los estudiantes por igual. Sin embargo, la autora lo plantea como un fenómeno claramente heterogéneo por el que los estudiantes se benefician o perjudican de manera diferente según las características de sus compañeros y el cual no tiene el mismo impacto en las diferentes etapas de escolarización. De hecho, los estudios que analizan el efecto pares en el rendimiento académico tienden a mostrar que los estudiantes más vulnerables se benefician en mayor medida de estar en aulas y escuelas con un mayor nivel socioeconómico de sus compañeros que los estudiantes menos vulnerables, a quienes no les afectan de manera determinante los efectos de los pares más vulnerables (Lugo, 2011; ^{Sacerdote, 2014}).

En todo caso, se han ofrecido múltiples explicaciones sobre por qué el efecto pares puede ser importante para el rendimiento de los estudiantes: que las capacidades, preferencias y actitudes de los estudiantes constituyan un recurso del proceso formativo en sí mismas (^{Krüger, 2018}; ^{Palardy, 2013}); la existencia de disparidades en el capital económico, social y cultural del alumnado (^{Li y Fischer, 2017}; ^{Torrents et al., 2018}); el llamado efecto contagio asociado con el cumplimiento de las normas, valores y comportamientos relacionados con la educación (^{Wilkinson, 2002}), entre otros.

El efecto pares y la incidencia de la segregación escolar sobre el rendimiento, a pesar de estar íntimamente relacionados, no son exactamente lo mismo. La investigación sobre el efecto pares observa la influencia del promedio del nivel socioeconómico de los compañeros del estudiante en el logro académico; mientras que la investigación sobre la incidencia de la segregación escolar se centra en el efecto de la concentración de estudiantes en función de su nivel socioeconómico. Es decir, en un caso importa el promedio del nivel socioeconómico de los compañeros, en otro el porcentaje de estudiantes de análogas características socioeconómicas. Más concretamente, en esta investigación se entiende como segregación de cada escuela la distancia entre la media geométrica de las participaciones de estudiantes de distinto nivel socioeconómico en ausencia de segregación y la media geométrica de las participaciones reales (^{Hutchens, 2001}; ^{Murillo, 2016}). En adelante, contemplando este matiz, recogemos aquellos trabajos que han analizado el impacto de la segregación en el rendimiento académico.

Pese a que son menos las investigaciones que estudian el impacto de la segregación escolar en el rendimiento académico, las evidencias científicas que se poseen defienden que estudiar en escuelas segregadas incide en el rendimiento académico de los estudiantes (^{Benito y González-Balletbò, 2014}; ^{Brandén et al., 2016}; ^{Murillo y Carrillo, 2021}; ^{Palardy, 2013}, 2020; ^{Owens, 2018}; ^{Reardon, 2016}; ^{Sciffer et al.,2020}; ^{Torrents et al., 2018}). De tal forma, que los estudiantes que asisten a escuelas con alta concentración de estudiantes de familias de bajo nivel socioeconómico obtienen menores resultados académicos de lo que sería previsible teniendo en cuenta el nivel socioeconómico de sus familias; mientras que asistir a una escuela con alta concentración de estudiantes de familias con más recursos hace que el rendimiento sea superior al previsto.

Entre otros, destaca el minucioso trabajo de ^{Reardon (2016}) quien evalúa numerosos registros de puntuaciones de exámenes de estudiantes de tercer a octavo grado de Educación Primaria, entre 2009 y 2012, de las escuelas públicas estadounidenses con el objetivo de obtener una mirada más a fondo entre la segregación racial y socioeconómica y las brechas de rendimiento. El autor examina dieciséis medidas distintas de segregación encontrando una clara evidencia de que la segregación está fuertemente correlacionada con las brechas de rendimiento netas en una amplia gama de covariables, lo que implica que las escuelas con una alta concentración de estudiantes con familias de bajo nivel socioeconómico son, en promedio, mucho menos eficaces que las escuelas con una mayor heterogeneidad de estudiantes.

Un trabajo similar lo realizan ^{Benito y González-Balletbò (2014}) quienes indagan sobre el impacto que pudiera tener una reducción de los niveles de segregación escolar en los resultados académicos globales de sistemas educativos similares. A partir de los datos de PISA 2009, realizan un ejercicio de simulación estadística creando dos escenarios hipotéticos: un escenario segregado y un escenario no segregado. Los resultados muestran claramente los logros en equidad de aquellos sistemas no segregados y, a su vez, destacan las diferencias porcentuales que alcanzan los hipotéticos sistemas educativos segregados y no segregados en las pruebas de rendimiento, llegando hasta casi un 40 % de diferencia en los resultados de rendimiento en lectura entre los diferentes escenarios. Resultados similares encuentran ^{Sciffer y sus colegas (2020}) en el sistema educativo australiano, afirmando que reducir la segregación socioeconómica de los estudiantes en las escuelas australianas no solo mejoraría la equidad en el crecimiento del rendimiento, sino que también aumentaría el crecimiento promedio del rendimiento del sistema escolar australiano.

Por último, se destaca el reciente estudio publicado por ^{Murillo y Carrillo (2021}) en el cual, a partir de un análisis multinivel, se estima la incidencia de la segregación por nivel socioeconómico en el rendimiento de los estudiantes de secundaria en tres áreas curriculares. Los resultados son determinantes: la segregación escolar por nivel socioeconómico afecta al rendimiento académico, de tal forma que la concentración de estudiantes con familias de menor nivel socioeconómico en la escuela hace que el rendimiento sea menor y que la concentración de estudiantes con familias de mayor nivel socioeconómico hace que el rendimiento mejore.

Segregación escolar en Uruguay

Muy recientemente se han publicado varios estudios que nos informan sobre la segregación escolar en Uruguay (^{Ferrando et al., 2020}; ^{INEEd, 2019}; ^{Murillo y Graña, 2020}; ^{Ramírez-Leira y Vazquez, 2020}). A pesar de ser uno de los países con una menor segregación promedio de América Latina (^{Murillo y Martínez-Garrido, 2017b}), el sistema educativo uruguayo tiene una segregación escolar por nivel socioeconómico de características muy especiales.

Así, según el estudio de ^{Murillo y Graña (2020}), Uruguay presenta una “baja” segregación (en términos relativos con los países de su entorno) para los estudiantes de familias con menos nivel socioeconómico, pero muy alta para los de familias con mayores recursos socioeconómicos. En la Figura 1, se muestra el perfil de segregación obtenido por estos autores, donde se ve con claridad este curioso fenómeno.

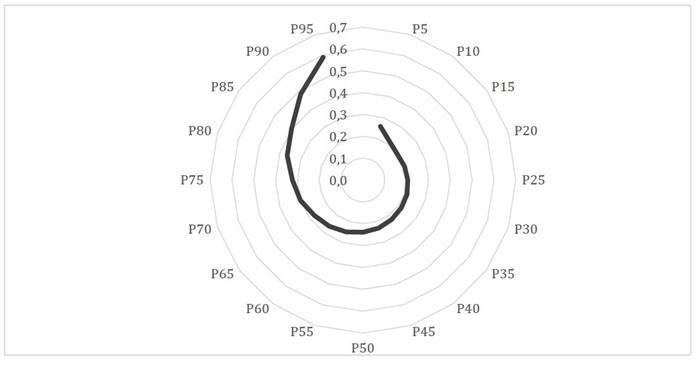
Fuente: Murillo y Graña (2020, p. 26).

Figura 1: Perfil de segregación escolar por nivel socioeconómico de Uruguay 

Este fenómeno se debe, según los autores, a la existencia de un sistema educativo público que ha apostado por el acceso universal junto con un sistema de educación privada de carácter elitista que acoge a los estudiantes con familias de mayores recursos. Además, desde el año 2003 al 2017, se detecta un aumento del 37 % en la segregación escolar según la titularidad del centro (^{Ramírez-Leira y Vazquez, 2020}). Es, por tanto, de especial interés mirar el efecto de la segregación escolar sobre el rendimiento en un sistema de estas características.

^{Ferrando y sus colaboradores (2020}), por su parte, muestran que los mayores niveles de segregación en las escuelas públicas de Uruguay se encuentran en Educación Inicial y Primaria, principalmente en las regiones del interior. Observan un incremento de la segregación en los últimos años, principalmente en Montevideo. Este dato es realmente preocupante para la calidad del sistema educativo uruguayo que, si bien ha mejorado el acceso, no puede obviar la problemática asociada a la segregación (^{Ferrando et al., 2020}).

Así, esta investigación busca determinar, en primer lugar, la incidencia de la segregación escolar sobre el rendimiento académico de los estudiantes de Educación Primaria de Uruguay. En segundo término, dada la relación entre la segregación y el efecto de los pares, se pretende determinar la incidencia de la segregación escolar en el rendimiento controlando el efecto pares.

Método

A partir de estos objetivos es posible formular las hipótesis de investigación:

H₁: Existen diferencias significativas en el rendimiento académico de los estudiantes de Educación Primaria de Uruguay en función de la magnitud de la segregación escolar del centro al que asisten.

H₂: Existen diferencias significativas en el rendimiento académico de los estudiantes de Educación Primaria de Uruguay en función de la magnitud de la segregación escolar del centro al que asisten, controlando el efecto pares.

Ello, a) tanto para tercer como para sexto grado de Educación Primaria, b) para rendimiento en matemática y en lectura y c) para cuatro consideraciones de segregación escolar. De esta forma se tienen 16 subhipótesis para cada una de las dos hipótesis principales.

Para validarlas o refutarlas se ha realizado una explotación de los microdatos de Aristas 2017 a través de Modelos Multinivel. Aristas es un Programa de Evaluación Nacional de Logros Educativos desarrollado por el Instituto Nacional de Evaluación Educativa de Uruguay (INEEd). Tiene como objetivo evaluar la calidad del sistema educativo uruguayo desde una perspectiva multidimensional, lo que implica evaluar el desempeño académico de los estudiantes, pero también incluir el análisis a los contextos sociales y familiares (^{INEEd, 2018}). Todo ello posibilita miradas que van más allá de las explotaciones que realiza el propio INEEd, como este caso.

Para esta investigación se utilizan las siguientes variables (algunas directamente estimadas por el INEEd y otras calculadas a partir de las anteriores para este trabajo), organizadas según su función:

-Variables dependientes: Rendimiento en Lectura y Rendimiento en Matemática, tanto en 3º grado como en 6º grado de Educación Primaria. Ambas variables fueron obtenidas mediante la Teoría de Respuesta al Ítem (TRI) y escaladas de tal forma que su media es 300 y su desviación típica de 50.

-Variables de ajuste: Nivel socioeconómico y cultural de las familias de los estudiantes (ESCS), variable tipificada y obtenida por el INEEd a partir de la zona geográfica donde se ubica la vivienda, la composición del hogar, la educación y la atención a la salud del principal sostenedor del hogar, características de la vivienda y elementos del confort del hogar, el nivel educativo de ambos padres o tutores de los estudiantes y la cantidad de libros con que cuenta el hogar (^{INEEd, 2018, p. 26}); el género del estudiante como variable dummy; y el nivel socioeconómico y cultural promedio de los estudiantes de la escuela, estimado ad hoc para esta investigación.

-Variables explicativas: Magnitud de la segregación nivel socioeconómico y cultural de cada escuela estimada a partir del Índice de Raíz Cuadrada de Hutchens con cuatro grupos minoritarios: el 10 % de estudiantes con familias de menor ESCS (P10), el 25 % de ellos o ellas (Q1), el 25 % de estudiantes de familias con mayor ESCS (Q4); y, por último, el 10 % de ellos o ellas (P10). El Índice de Raíz Cuadrada de Hutchens (H) para cada escuela i se estima de la siguiente forma (^{Hutchens, 2001}):

Donde, para Uruguay, x_1i y x_2i representan el número de alumnos del grupo minoritario y mayoritario, respectivamente en la escuela i. X₁ y X₂ son el número total de estudiantes de los grupos minoritario y mayoritario en todas las escuelas del país. De esta forma, con este índice, para cada escuela, se mide la distancia entre la media geométrica de las participaciones de estudiantes de distinto nivel socioeconómico en ausencia de segregación y la media geométrica de las participaciones reales.

La muestra del estudio está conformada por 15.355 estudiantes, prácticamente la mitad de tercer grado de educación primaria y la otra mitad de sexto grado (7.694 y 7.661, respectivamente), que estudian en 247 escuelas. Para la selección de la muestra, Aristas realiza un diseño muestral con selección aleatoria sistemática de estratos previamente definidos en relación con el tamaño de las escuelas y con subestratificación por contexto y categoría de las escuelas. Con esa base se realiza una selección trietápica donde, en primer lugar, se eligen escuelas de manera aleatoria dentro de los estratos; en segundo lugar, se seleccionan grupos dentro de las escuelas; y, en tercer lugar, se seleccionan todos los estudiantes de los grupos escogidos. En este marco muestral quedan integrados todos los centros educativos públicos y privados de Uruguay con al menos un estudiante de tercer y sexto grado de Educación Primaria. Finalmente, en Aristas 2017 participaron 247 de las 251 escuelas seleccionadas, por lo que se logró una cobertura de 98,4 %.

Se estimaron Modelos Multinivel de dos niveles (estudiante “i” y escuela “j”) para determinar si existen diferencias significativas en el rendimiento en cada una de las dos áreas (matemática y lectura) en función de la segregación escolar (con las cuatro consideraciones de esta), controlando las variables que pueden incidir en la relación. Es importante tener en cuenta que el uso de modelos multinivel no permite acercarse al fenómeno como un efecto causal, debido a las múltiples fuentes de endogeneidad que confluyen en un proceso tan complejo, así como las interacciones mutuas. Pero sí muestra la incidencia, por lo que este trabajo se limita a mostrar la incidencia de la segregación sobre el rendimiento.

El proceso de modelado multinivel realizado tanto para 3er grado como para 6º y para cada uno de los rendimientos, es el siguiente:

Modelo A1, sólo con las variables de ajuste:

Modelos A2, añadiendo individualmente cada una de las cuatro variables explicativas al modelo de ajuste (modelo 1)

Para validar/refutar la segunda hipótesis, se incorpora el nivel socioeconómico y cultural de las familias de los estudiantes promedio de la escuela como variable de ajuste. De esta manera, se obtiene:

Modelo B1, sólo con las variables de ajuste:

Modelos B2, añadiendo individualmente cada una de las variables explicativas al modelo de ajuste (modelo 1b):

Donde, para cada estudiante “i” escuela “j”, β 0 representa la puntuación media del rendimiento en cada una de las dos áreas analizadas, β 1j y β 2j son las pendientes de las dos variables de nivel estudiante ESCS de la familias y género, y β 3j y β 4j son las diferentes pendientes de las variables de segregación y de ESCS promedio de la escuela. μ 0j es el error asociado a cada escuela “j” y ε ij es el error asociado cada estudiante “i” de la escuela “j”.

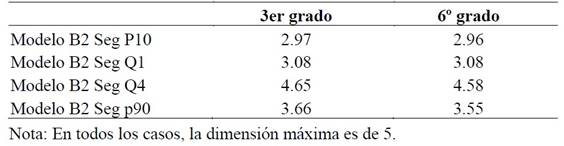
Además, dada la relación entre el efecto pares y la segregación, se ha estimado del Índice de Condición (IC) para descartar la condición de multicolinealidad que podría producirse al incluir en el modelo el promedio del nivel cultural de las familias y las diferentes variables referidas al valor de la segregación escolar por nivel socioeconómico para cada uno de los cuatro grupos minoritarios. Así, los valores obtenidos de la estimación del IC para la dimensión máxima (5) varía entre 2,96 y 4,65 (ver Tabla 1). Dado que se considera la existencia de multicolinealidad a partir de un valor de 20 (^{Belsey, 1982}) es posible descartar esta condición en los modelos multinivel estimados.

Tabla 1: Análisis de colinealidad de los modelos multinivel 

Fuente: Elaboración propia a partir de Aristas 2017.

Resultados

Se presentan en primer lugar, los resultados correspondientes a los estudiantes de 3er grado, inicialmente para rendimiento en matemática y posteriormente en lectura. El segundo apartado muestra los resultados para los estudiantes de 6º grado.

Incidencia de la segregación en el rendimiento en 3er grado

Los resultados del proceso de Análisis Multinivel para 3er grado de Educación Primaria, tanto para rendimiento en matemática (Tabla 1), como en lectura (Tabla 2) validan la primera hipótesis: Existen diferencias significativas en el rendimiento académico de los estudiantes de Educación Primaria de Uruguay en función de la magnitud de la segregación escolar del centro al que asisten. Los resultados acerca de la segunda hipótesis, sin embargo, no ofrecen resultados tan claros. Concretamente se ha encontrado que, controlando el nivel socioeconómico promedio de la escuela, un proxy del efecto pares, la segregación escolar incide en el rendimiento solo para la segregación de los estudiantes con familias de más recursos; y, además, empeora los resultados de los estudiantes.

Dada la gran cantidad de datos obtenidos, para facilitar la comprensión se mostrará en primer lugar el proceso de modelado multinivel para estudiantes de tercer grado primero para rendimiento en matemática y luego para rendimiento en lectura. En ambos casos, para analizar la hipótesis 1 y la 2, se han realizado dos procesos de modelado multinivel, primero sin incluir el nivel socioeconómico promedio de la escuela (modelos A) y después incluyéndolo como variable de control (modelos B).

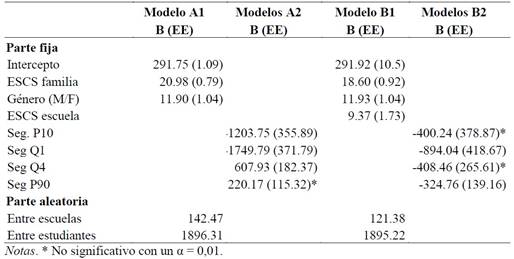
Los resultados del proceso de modelado para el rendimiento en matemática (Tabla 1) muestran, en primer lugar (modelo A1), que las dos variables de control (género y nivel socioeconómico del estudiante) cumplen su función, dado que inciden en el rendimiento académico de los estudiantes. Así, por cada desviación típica en la que el nivel socioeconómico del estudiante sea más alto (o más bajo), su rendimiento será de 22,15 puntos más alto (o bajo), lo que significa 0,44 puntuaciones típicas. También muestran, que las estudiantes mujeres obtienen de promedio 3,90 puntos más que sus compañeros varones.

Tras introducir por separado cada una de las cuatro consideraciones de segregación (modelo A2), se observa que las cuatro hacen una aportación estadísticamente significativa al modelo. La segregación escolar para el 10 % de los estudiantes con familias de menos nivel sociocultural y para el 25 % de estos (P10 y Q1) hace una aportación negativa. Eso significa que estudiar en una escuela segregada hace que el rendimiento de los estudiantes se vea disminuido. Para la segregación con el 25 % de los estudiantes con familias de mayor nivel sociocultural y para el 10 % de ellos (Q4 y P90) las pendientes son positivas, lo que significa que los estudiantes escolarizados en escuelas segregadas de mayor nivel socioeconómico obtienen mejor rendimiento y que los que no lo están, considerando el género y el nivel socioeconómico de las familias. Es un primer e interesante resultado.

Es más, si se analiza la varianza explicada por cada una de las variables explicativas a partir del modelo ajustado, se observa que la segregación para el P10 explica el 3,27 % de la varianza del centro, para el Q1 explica el 6,73 %, para el Q4 lo hace el 13,16 % y, por último, para el P10 lo hace el 3,26 %. Eso significa que, sin controlar el nivel socioeconómico promedio del centro, la consideración de segregación que más incide en el rendimiento en matemática es la segregación escolar con el grupo minoritario del 25 % de los estudiantes de familias con mayor nivel socioeconómico.

En el segundo proceso de modelado (modelos B), para validar la hipótesis 2, se ha incluido la variable “nivel socioeconómico promedio de la escuela” como variable de ajuste. La influencia del nivel socioeconómico promedio sobre el rendimiento (el efecto pares). De esta forma, se pretende descontar su influencia en la incidencia de la segregación en el rendimiento. Los resultados (Tabla 2) indican, en primer término, que esta nueva variable del nivel socioeconómico promedio de la escuela hace una aportación significativa en el modelo solo con las variables de ajuste. Efectivamente por cada desviación típica que sea más alto que el nivel socioeconómico promedio del grupo donde está el estudiante, el rendimiento será 0,25 desviaciones típicas más alto o más bajo el rendimiento del alumno (12,51 puntos), controlando por género y el nivel socioeconómico de la familia del estudiante. Con ello, se demuestra la existencia del efecto pares y su fuerte influencia en el aprendizaje de los estudiantes.

Como se puede observar en los modelos B2, la incorporación de la variable nivel socioeconómico promedio de la escuela (junto con el género y el nivel socioeconómico de la familia del estudiante) y las aportaciones de las cuatro consideraciones de segregación escolar varían de forma muy importante. Efectivamente, de las cuatro analizadas, tres de ellas dejan de hacer una aportación estadísticamente significativa al modelo. Es decir, la segregación escolar para el P10, para el Q1 y para el Q4 no inciden en el rendimiento en matemática si se controla el efecto pares. Sin embargo, si lo hace la segregación para el P90 y, curiosamente, cambia su sentido. Su aportación ya no es positiva sino negativa. Dicho de otro modo, los estudiantes que asisten a una escuela segregada para el 10% de los que tienen mayores recursos, se ven perjudicados por ese hecho. Es decir, la segregación escolar tiene efectos negativos sobre el rendimiento hasta para los estudiantes con más recursos.

Tabla 2: Procesos de modelado multinivel para rendimiento en matemática de estudiantes de tercer grado de Educación Primaria 

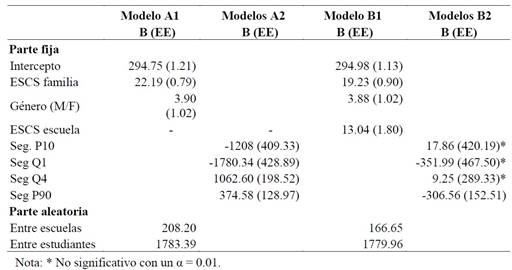
Fuente: Elaboración propia a partir de Aristas 2017.

Los resultados con la variable explicada (o dependiente) sobre el rendimiento en lectura ofrece resultados análogos a los encontrados para rendimiento en matemática. Podemos resumirlos en cinco elementos (Tabla 3):

1.El nivel socioeconómico de las familias y el género inciden en el rendimiento en Lectura, de tal forma que es adecuado incluirlas como variables de ajuste para controlar su efecto. Llama la atención que las estudiantes mujeres obtienen 12,5 puntos más que sus compañeros varones, cifra muy superior a la encontrada para rendimiento en matemática.

2.En los modelos A, sin incluir el nivel socioeconómico promedio de las familias de la escuela, las cuatro consideraciones de segregación escolar inciden en el rendimiento en Lectura. Con el mismo sentido que se había encontrado para rendimiento en matemática: negativo para el P10 y Q1 y positivo para el Q4 y P10. Los valores de estos cuatro coeficientes son aproximadamente los mismos que para rendimiento en Lectura. Luego estudiar en una escuela segregada incide en el rendimiento en Lectura para los estudiantes de 3er grado. La varianza del rendimiento del nivel escuela explicada por cada una de las consideraciones es análoga a la encontrada en matemática: de 1,75 % para el P90, 4,6 % para Q1, 11, 20 % para Q4 y 3,82 % para P10, algo más baja en todos los grupos excepto para el P90.

3.Se verifica el efecto pares también para rendimiento en lectura. Existe una influencia estadísticamente significativa del nivel socioeconómico promedio de la escuela en el rendimiento en Lectura, controlado por el nivel socioeconómico del estudiante y su género.

4.La incidencia de la segregación escolar, controlando el efecto pares, es estadísticamente significativa solo para la consideración de segregación del 10 % de los estudiantes con familias con más recursos, y esta es negativa.

Tabla 3: Procesos de modelado multinivel para rendimiento en lectura de estudiantes de tercer grado de Educación Primaria 

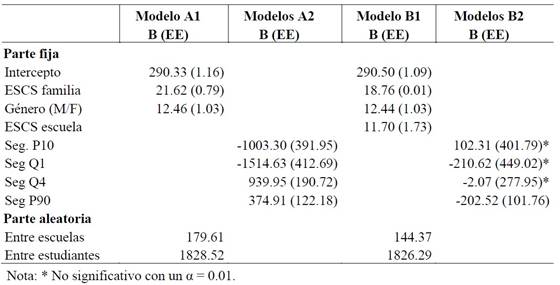
Fuente: Elaboración propia a partir de Aristas 2017.

Con todo ello se ha visto que los resultados de la investigación para rendimiento en matemática y en lectura para tercer grado son absolutamente coherentes, solo variando la magnitud de algún índice, pero no cambia en nada el sentido global.

Incidencia de la segregación en el rendimiento en 6º grado

El estudio de la incidencia de la segregación escolar en el rendimiento académico en 6º grado de Educación Primaria ofrece grandes analogías, pero también importantes matices, frente a lo encontrado para tercer grado. En primer lugar, una vez más, comenzamos con el rendimiento en matemática.

Los resultados del proceso de modelado multinivel con la variable explicada rendimiento en matemática se reflejan en la Tabla 4. Para los modelos sin la variable “Nivel socioeconómico promedio de la escuela” (modelos A), es posible observar que, de las dos variables de ajuste, solo el Nivel socioeconómico de las familias cumple su misión de control. El género no incide en el rendimiento en matemática de los estudiantes de 6º grado.

En los modelos A2, con las variables de ajuste incluidas individualmente, se encuentra que las cuatro consideraciones de segregación escolar analizadas hacen una aportación estadísticamente significativa al modelo. De esta forma, se puede concluir que la segregación tiene un efecto claro sobre el rendimiento en matemática de los estudiantes de 6º grado. Asimismo, al igual que lo hallado hasta ahora, esa incidencia es negativa para el P10 y el Q1 y positiva para el Q4 y P90. Hasta el momento los resultados son muy parecidos a los encontrados para tercer grado. La diferencia radical es que la varianza explicada es mayor: 5,56 % para P10, 9,60 % para Q1, 19,07 % para Q4 y 10,41 % para P90. Con estos resultados se valida la hipótesis 1 para estudiantes de 6º grado y rendimiento en matemática.

Las novedades respecto a 3er grado aparecen en la validación de la hipótesis 2, es decir, cuando se incorpora la variable NSEC promedio de la escuela. El modelo solo con las variables de ajuste (B1) indica que es mayor la influencia de esta variable en el rendimiento en matemática que lo detectado en tercer grado. El valor del coeficiente de NSEC de la escuela es de 15,6, frente al 11,7 en tercero. Ello indica que el efecto pares es más fuerte en sexto que en tercero.

Cuando se introducen, de forma independiente cada una de las cuatro consideraciones de segregación escolar, los resultados nos dicen que, en este caso, ninguna de las variables hace una aportación significativa al modelo ajustado. Es decir, controlando el efecto pares, la segregación no tiene efecto en el rendimiento en matemáticas en estudiantes de sexto curso.

Tabla 4: Procesos de modelado multinivel para rendimiento en matemática de estudiantes de sexto grado de Educación Primaria 

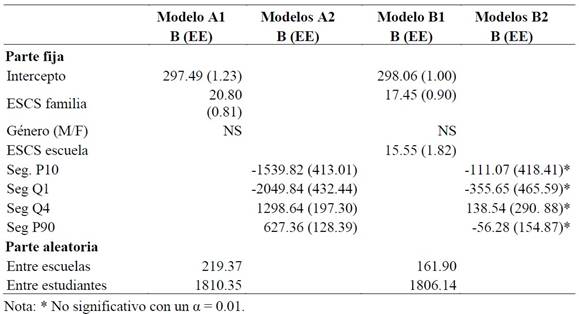
Fuente: Elaboración propia a partir de Aristas 2017

El último de los cuatro análisis previstos analiza la influencia de la segregación en el rendimiento en lectura para los estudiantes de sexto, en primer lugar, sin tener en cuenta el nivel socioeconómico promedio de la escuela (hipótesis 1) y, después, considerándolo (hipótesis 2).

Los resultados (Tabla 5) muestran grandes analogías con los anteriores, pero también ciertos matices. En primer lugar, para los modelos A, la variable nivel socioeconómico y cultural de las familias del estudiante y su género inciden en el rendimiento, luego cumplen su función como variables de control. Sin embargo, no todas las consideraciones de segregación tienen incidencia. En este caso, la variable Segregación escolar por nivel socioeconómico para el 10 % de estudiantes de familias con más recursos no hace una aportación significativa al modelo: no parece incidir en el rendimiento. La varianza del centro explicada por las otras tres consideraciones de segregación son 5,00 % para P10, 10,91 % para Q1 y 4,03 % para Q4.

Para los modelos B se descubren varios resultados interesantes. En primer lugar, se encuentra que el efecto par parece ser más bajo que para rendimiento en matemática y para tercer grado. Y ese menor efecto hace que, al incluir las variables independientes (las cuatro consideraciones de segregación), dos de ellas hagan aportaciones significativas al modelo. La segregación para el P90, como ya se encontró en tercer grado, y la segregación para Q1. En ambos casos, estudiar en una escuela segregada hace que los resultados de los estudiantes sean más bajos que si la escuela no está segregada.

Tabla 5: Procesos de modelado multinivel para rendimiento en lectura de estudiantes de sexto grado de Educación Primaria 

Fuente: Elaboración propia a partir de Aristas 2017

Conclusiones

Esta investigación ha buscado validar/refutar dos hipótesis: H1: Existen diferencias significativas en el rendimiento académico de los estudiantes de Educación Primaria de Uruguay en función de la magnitud de la segregación escolar del centro al que asisten; y H2: Existen diferencias significativas en el rendimiento académico de los estudiantes de Educación Primaria de Uruguay en función de la magnitud de la segregación escolar del centro al que asisten, controlando el efecto pares. Todo ello, tanto para tercer como para sexto grado de Educación Primaria, para rendimiento en matemática y en lectura y para cuatro consideraciones de segregación escolar.

Los resultados son claros en validar la primera de las hipótesis, pero muestra muchos matices respecto a la segunda.

Efectivamente, este trabajo ha encontrado, en primer lugar, que la segregación escolar por nivel socioeconómico incide de forma clara en el rendimiento académico de los estudiantes uruguayos de Educación Primaria. Este hecho ha sido demostrado empíricamente para los dos grados analizados (tercero y sexto), para rendimiento en matemática y en lectura, y para las cuatro consideraciones de segregación escolar (P10, Q1, Q4 y P90 como grupos minoritarios). Con más precisión, se ha encontrado que estudiar en un centro que concentra estudiantes más vulnerables hace que el rendimiento de los estudiantes sea más bajo que el de sus compañeros que están en centros no segregados. Y, que estudiar en un centro con alta concentración de estudiantes con familias de más recursos hace que los estudiantes obtengan mejor rendimiento que el de sus pares en escuelas no segregadas, todo ello controlando el género y el nivel socioeconómico de las familias de los estudiantes.

Los resultados, sin embargo, muestran que la validación de la segunda hipótesis no es tan clara, sino que depende del curso de los estudiantes, de área de rendimiento y de la consideración de segregación utilizada. Así, con carácter general, se puede afirmar que la segregación escolar por nivel socioeconómico en Uruguay incide en el rendimiento después de controlar el efecto pares, pero solo para la segregación del 10 % de los estudiantes con familias de mayor nivel socioeconómico. Y, en esas circunstancias, estudiar en un centro segregado, hace que el resultado sea peor que si no lo estuviera. Estos resultados, se corresponden a la perfección en los estudiantes de tercer grado, para sexto es un poco más complejo, dado que para matemática no incide la segregación controlando el efecto pares en ningún caso, y para el rendimiento en lectura incide tanto para el 25% de los estudiantes con familias con menos recursos, como para el 10% de los estudiantes de familias con más recursos.

Estos resultados son coherentes, en primer lugar, con los estudios que muestran la influencia de la segregación escolar en el rendimiento de los estudiantes. Efectivamente, es coincidente con trabajos como ^{Brandén y colaboradores (2016}), ^{Reardon (2016}), ^{Murillo y Carrillo (2021}), ^{Oberti y Savina (2019}), ^{Vivian (2017}), entre otros; y es coincidente con ello en el sentido de que el rendimiento de los estudiantes se ve perjudicado al estudiar en escuelas de alta concentración de estudiantes más vulnerables, pero es beneficioso al estudiar en escuelas con alta concentración de estudiantes socioeconómicamente favorecidos. No hay estudios, sin embargo, que descuenten el efecto pares de la influencia de la segregación, por lo que no es posible comparar estos resultados con otros trabajos. Tampoco es fácil determinar si los resultados son debidos a ser datos de Uruguay; este país, recordemos, se caracteriza por tener una baja segregación para los estudiantes más vulnerables, pero especialmente alta para los estudiantes de más recursos. Sería importante hacer más estudios que profundizaran en estos resultados, especialmente el llamativo resultado de que estudiar en un centro con alta concentración de estudiantes de familias con mayor nivel socioeconómico, controlando el efecto pares, tenga un efecto negativo en el rendimiento de los estudiantes. Estos resultados tienen unas claras implicaciones para la toma de decisiones. Así, como ya se sabía, la segregación escolar tiene una fuerte incidencia en el rendimiento académico, especialmente entre los estudiantes más vulnerables. Siendo un claro factor de inequidad con el que hay que luchar de forma prioritaria. El resultado de que la alta concentración de estudiantes de familias con más recursos incide negativamente en el rendimiento de los estudiantes, habiendo descontado el efecto pares, es un resultado especialmente interesante para Uruguay. Si Uruguay quiere mejorar el rendimiento académico de sus estudiantes debe atajar esos altos niveles de segregación escolar para los estudiantes más favorecidos. Tanto por el bien de estos alumnos como de todo el conjunto educativo. Sin entrar en el tema de la adecuada socialización, o de la formación en valores o las ventajas de ser educado en la diversidad. Acabar con la segregación es una obligación de cualquier sistema educativo que realmente busque que sus estudiantes aprendan. Uruguay no puede conformarse con tener un buen sistema educativo público, acabar con estas escuelas de élite es también una obligación.

La presente investigación, al haber usado datos proporcionados por la propia administración uruguaya y con unas altas exigencias de calidad, obtiene resultados altamente fiables. Su alcance, sin embargo, se restringe a la validación o refutación de cada una de las 32 subhipótesis definidas. El establecimiento de relaciones de causa-efecto, por tanto, quedan fuera, dejándolo como simples ideas para futuras investigaciones. También esta investigación tiene como limitación el centrarse en educación primaria y en un país como Uruguay con una alta segregación para los grupos de escolares de familias con más recursos. Esta línea de trabajo ofrece, con ello, interesantes pero incipientes resultados que sin duda necesitarían una mayor profundización.

Así, sería interesante, en primer lugar, replicar la investigación para países con una segregación alta para todos los estudiantes y alta para los estudiantes de menos recursos. Pero, sobre todo, es necesario avanzar en buscar las razones de esta relación segregación-rendimiento. También es necesario una mayor investigación sobre las medidas a tomar por las Administraciones Públicas para acabar con la segregación.

La segregación escolar delimita el establecimiento de vínculos entre personas de diferentes características sociales y personales, lo que ya de por si supone un obstáculo para la generación de actitudes positivas hacia la diversidad y una barrera para luchar contra la inclusión y la cohesión social. Pero va más allá ya que, como se ha visto en este estudio, la segregación acentúa la brecha en el aprendizaje académico de los estudiantes, lo que la convierte en una potente herramienta de exclusión social. Tal y como afirman ^{Murillo y Martínez-Garrido (2020}), la segregación escolar no es un efecto colateral indeseado sino un acto totalmente consciente de aquellos que impulsan sistemas educativos de élite en detrimento de sistemas educativos públicos de calidad para todos y todas las estudiantes. No se puede perseguir una sociedad socialmente justa e inclusiva sino se toman acciones políticas para luchar en contra la injusticia.