Introducción
Los sistemas de salud necesitan información confiable sobre su funcionamiento y performan ce para tomar decisiones correctivas o de mejora de procesos e infraestructura, así como para la adecuación de los esfuerzos económicos. En las últimas décadas la relevancia de tomar decisio nes con base en indicadores validados ha venido creciendo de manera exponencial con el objetivo principal de evaluar los resultados clínicos y po der compararlos con parámetros internacionales y entre diferentes centros a nivel nacional1-5.
La mortalidad posoperatoria ha sido el indica dor principal de los resultados a corto y mediano plazo en la evaluación de la cirugía cardíaca, si bien existen otras medidas de resultado que cuan tifican morbilidad y requerimientos de Unidad de Cuidados Intensivos (UCI)6. Es una condición fundamental de lo dicho previamente poder desa rrollar análisis que ajustan por riesgo, en lugar de analizar el evento con frecuencias crudas, por lo que se han desarrollado diferentes modelos de riesgo. De estos, los más utilizados son los mode los logísticos6.
Los modelos de ajuste del riesgo identifican variables que predicen el riesgo de sufrir un de terminado evento, por ejemplo, muerte o reinter vención. En particular, un modelo de regresión logística binaria se usa para predecir el compor tamiento de una variable dependiente como la muerte posoperatoria en función de una serie de variables independientes o explicativas que son factores protectores o de riesgo para el evento. La predicción consiste en la determinación de una probabilidad de muerte que es usada para calcular el número de muertes esperadas (ME) y compararlo con el número de muertes observadas (MO), generalmente construyendo un indicador de razón (MO/ME)7,8.
El desarrollo de un modelo de regresión logís tica conlleva una serie de pasos muy bien descri tos en libros técnicos, donde algunas de las princi pales referencias son Hosmer y Lemeshow (2013) y Steyerberg (2019)(9,10. Dos etapas principales pueden reconocerse en dicho desarrollo. La prime ra es de validación interna en la que se evalúan las propiedades del modelo con base en los datos con los que fue generado en ka la población origi nal. La segunda etapa es la de validación externa, donde se evalúan las mismas propiedades en da tos que no se utilizaron para generar el modelo. La elaboración de una herramienta adecuada im plica ambos pasos de validación; la discriminación y la calibración son las propiedades a evaluar.
La discriminación es la capacidad que tiene el modelo predictivo en identificar aquellos indivi duos que tuvieron el evento de aquellos que no lo tuvieron9,11.
La calibración se refiere a cuantificar si la dife rencia entre los casos observados para determina do evento (por ejemplo, la muerte) es diferente a los casos esperados (mortalidad predicha) en una cantidad determinada de estratos, por ejemplo, deciles de riesgo9,12.
En particular en cirugía cardíaca se han de sarrollado varios modelos de este tipo. Algunos ejemplos son: Parsonnet (EE. UU.), Tu (Canadá), Roques (Francia), Pons (España), EuroSCORE I y II (predominan países europeos), STS (EE. UU.) y SPScore (Brasil)5,6,13-18. Entre ellos, uno de los más conocidos y aplicados es el EuroSCORE I (European System for Cardiac Operative Risk Evaluation) para predecir la mortalidad operato ria1,2. Allí, la mortalidad operatoria fue definida como la muerte dentro de los 30 días posteriores a la operación o dentro del mismo ingreso hospita lario de la cirugía1.
El EuroSCORE I proporciona la probabilidad de morir de cada individuo a partir de 18 varia bles de riesgo y con un coeficiente beta asociado a cada una de ellas2,7. Este modelo fue creado y validado inicialmente en un estudio de 19.030 pacientes europeos intervenidos en el año 1995; existió además de la variante logística un modelo más simple denominado EuroSCORE aditivo que adjudica un peso determinado a cada factor de riesgo que presenta el paciente. La suma de esos pesos proporciona la probabilidad aproximada de morir.
El Fondo Nacional de Recursos (FNR) tiene como uno de sus cometidos el de evaluar los resul tados de los actos financiados; hay una unidad es pecífica para ello, la Unidad de Evaluación. En lo que refiere a la evaluación de la cirugía cardíaca de adultos en Uruguay el FNR utiliza un EuroS CORE I ajustado a la población 2003-2006 desde el año 2007 y los resultados se publican anual mente en la página web de la institución (http:// www.fnr.gub.uy/publicacionesFNR_).
El objetivo de este trabajo es el de presentar los resultados de la aplicación y validación del mo delo EuroSCORE I logístico en Uruguay entre los años 2003 y 2020.
Metodología
Inicialmente se desarrolló una validación externa del EuroSCORE I en la población uruguaya adul ta (edad ≥ 18 años) intervenida de cirugía cardía ca en procedimientos financiados por el FNR en tre los años 2003 a 2006.
Se excluyeron aquellos pacientes en los que no se logró encontrar información para construir alguna de las variables del EuroSCORE I. En tal sentido, un 8% del total de pacientes fueron ex cluidos del análisis, ya que faltaban datos de al menos una variable.
Una vez que se validó el EuroSCORE I, este se aplicó prospectivamente entre 2007 y 2020 en su versión original y con el ajuste desarrollado con la población del período 2003-2006.
Para la construcción del riesgo individual se utilizaron como definiciones operacionales aque llas recomendadas por el EUROSCORE origi nal1,2. Los datos analizados fueron obtenidos de: a) los formularios de solicitud y realización de cirugía cardíaca de adultos que son enviados al FNR por los médicos tratantes y por el cirujano que realiza la cirugía; y b) datos de mortalidad obtenidos por Registros Médicos del FNR. Toda la información de los formularios referidos y de la mortalidad se ingresa en el sistema informático del FNR.
Análisis estadístico
En primer lugar, se elaboró mediante programa ción una sintaxis para construir las variables del EuroSCORE I a partir de la base de datos del FNR. Posteriormente se calculó la mortalidad esperada (ME) aplicando el modelo logístico del EuroSCORE I original a cada paciente y se obtuvo la probabilidad de muerte individual. Se realizó la suma de las probabilidades individuales, y se obtuvo así el número total de muertes esperadas para el grupo de pacientes considerados. Luego, se calculó la razón MO/ME para el modelo origi nal con el dato de muerte dentro de los primeros 30 días posteriores a la cirugía cardíaca.
La discriminación y la calibración del mode lo logístico EuroSCORE I fueron analizadas me diante el área bajo la curva ROC y el test de Hos mer-Lemeshow9,11.
Se realizó una recalibración empleando la re gresión logística e incluyendo como variable inde pendiente el logit del EuroSCORE original y como variable dependiente la mortalidad a 30 días10,12. Para el cálculo del logit ajustado a la población uruguaya operada de cirugía cardíaca entre el 1 de enero de 2003 y el 31 de diciembre de 2006, se tomaron los valores de los coeficientes α y α 0 de dicha regresión, y se calculó según la siguiente fórmula: logit ajustado = α 0 + α * logit original.
Con el nuevo logit se calculó la probabilidad ajustada de muerte individual, según la fórmula habitual: probabilidad = e logit ajustado/(1 + e logit ajustado).
Para la razón MO/ME, el intervalo de confian za al 95% (IC 95%) se estimó según la siguiente fórmula: MO/ME ± 1,96 x (√Σ(p x q))/ME, donde p = probabilidad individual de morir estimada por score logístico y q = probabilidad individual de vi vir estimada por score logístico(8).
Los análisis fueron realizados en el transcu rrir de los años con los programas SPSS 11.0 y distintas versiones de STATA (actualmente la 17.0). Se consideró un nivel estadísticamente sig nificativo cuando el valor p fue menor a 0,05.
Los individuos intervenidos han aprobado me diante consentimiento informado el uso de sus da tos personales.
Resultados
En la figura 1 se puede observar la evolución de la MO, la ME y la relación MO/ME, donde la ME fue calculada con base en el EuroSCORE I original y el período de estudio fue 2003-2020. Se observan 5 años en los que la MO/ME fue significativamente mayor que 1 y, por tanto, la mortalidad observada fue mayor que lo pronosticado por el modelo.
En la tabla 1 se puede observar la evolución de los indicadores de discriminación y calibración del modelo original, así como el valor de la razón MO/ME y su intervalo de confianza para el perío do 2007-2020.
Como se puede observar, para el año 2007 el modelo original no calibró en forma adecuada (test Hosmer-Lemeshow), por lo que para ese mis mo año se realizó el ajuste del modelo como se des cribe en la sección de metodología tomando como referencia la población del período 2003-2006.
Los nuevos coeficientes para el cálculo de la probabilidad ajustada (logit ajustado EuroSCO RE I recalibrado) fueron los siguientes: logit ajus tado = - 0,3711694711681 + 0,8198157555571 * logit original.
Estos mismos coeficientes son los que se si guieron aplicando para el cálculo del modelo ajus tado o recalibrado hasta el año 2020 y cuyos prin cipales resultados se muestran en la tabla 2.
En la tabla 3 se puede observar la evolución de la prevalencia de las variables del EuroSCO RE I entre los años 2003 y 2020. Los porcentajes de mortalidad esperada de la tabla 3 son para el modelo ajustado (o recalibrado).
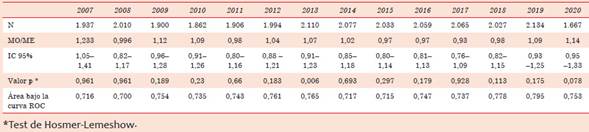
Tabla 2. Principales indicadores de la performance del modelo aplicando el EuroSCORE I recalibrado a la población uruguaya intervenida en el período 2003-2006.
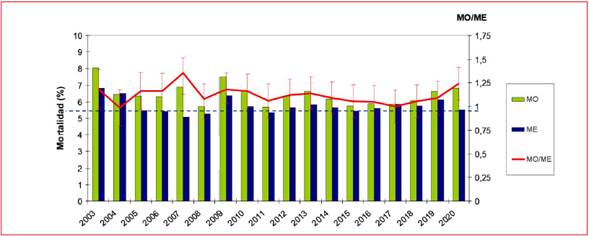
Figura 1. Evolución nacional de la relación mortalidad observada/esperada ajustada por EuroSCORE I original (2003-2020).
Como se puede observar, para el año 2007 el modelo original no calibró en forma adecuada (test Hosmer-Lemeshow), por lo que para ese mis mo año se realizó el ajuste del modelo como se des cribe en la sección de metodología tomando como referencia la población del período 2003-2006.
Los nuevos coeficientes para el cálculo de la probabilidad ajustada (logit ajustado EuroSCO RE I recalibrado) fueron los siguientes: logit ajus tado = - 0,3711694711681 + 0,8198157555571 * logit original.
Estos mismos coeficientes son los que se si guieron aplicando para el cálculo del modelo ajus tado o recalibrado hasta el año 2020 y cuyos prin cipales resultados se muestran en la tabla 2.
En la tabla 3 se puede observar la evolución de la prevalencia de las variables del EuroSCO RE I entre los años 2003 y 2020. Los porcentajes de mortalidad esperada de la tabla 3 son para el modelo ajustado (o recalibrado).
Discusión
Las escalas de riesgo son herramientas metodoló gicas y estadísticas que tienen varias utilidades entre las que podemos destacar: a) uso como es tándar externo contra el cual comparar los resul tados en una población diferente a la original; b) como un estándar interno, cuando se comparan grupos (por ejemplo, instituciones, Instituto de Medicina Altamente Especializada ;IMAE, etc.) en la población en la cual se desarrolló la escala o luego de validarlo para otra población; c) la toma de decisiones en la práctica clínica, consideran do el riesgo quirúrgico; d) información adecuada para el consentimiento informado.
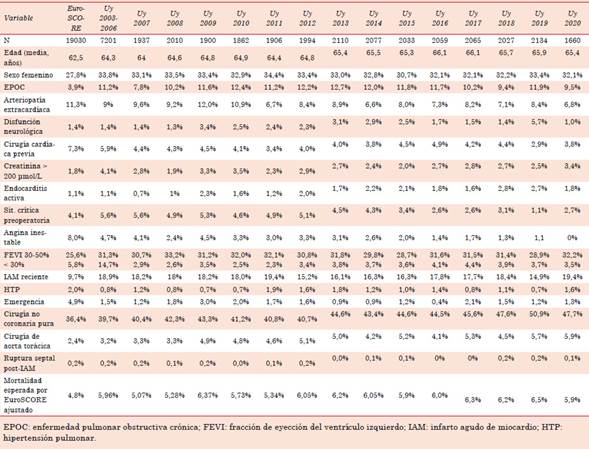
Tabla 3. Modelo logístico de ajuste del riesgo de Mortalidad Operatoria EuroSCORE I. Factores incluidos en el EuroSCORE I y prevalencia de factores.
En el caso de utilizarlo como estándar externo no hay que validar el modelo, ya que se calcula directamente la relación MO/ME y se observa si el valor encontrado es significativamente superior a 1 (mortalidad observada superior a la esperada), si es significativamente inferior a 1 (mortalidad observada inferior a la esperada) o si no difiere significativamente de 1 (mortalidad observada dentro de los límites esperados para esa pobla ción). En este caso, el valor 1 de MO/ME corres ponde al de la performance quirúrgica (en el ejem plo del EuroSCORE I) de los equipos de cirujanos cardíacos europeos que operaron a una determi nada población en un momento dado (en el caso del EuroSCORE I, la población europea de 1995).
Para el caso del estándar interno, es funda mental chequear la performance del modelo en cuanto a la calibración y la discriminación. Si el test de calibración (test de Hosmer-Lemeshow) es significativo, entonces hay que calibrar el modelo ajustándolo a la mortalidad de nuestra población. Es importante destacar que la discriminación siempre será la misma (tanto en el modelo origi nal como en el ajustado). En el caso de nuestro trabajo, como se puede observar en la tabla 1, para el año 2007 el valor p del test de Hosmer-Lemes how fue significativo, eso nos obligó a buscar una población de referencia para ajustar el modelo de riesgo. Una opción posible podría haber sido elegir el mismo año 2007 (de hecho, eso también se hizo en años subsiguientes), aunque en ese momento se optó por otro camino: elegir una población más numerosa e inmediatamente anterior al año eva luado (población uruguaya intervenida por cirugía cardíaca en los años 2003 a 2006). Como se puede observar en la tabla 2, el modelo ajustado para el año 2007 calibró de forma adecuada (p = 0,961).
Posteriormente ese fue el modelo que se aplicó para la comparación interna hasta el 2020, como se observa en la tabla 2, salvo en 2013, año en el que el modelo ajustado no calibró en forma sa tisfactoria. En todos los años evaluados el modelo mostró una capacidad discriminativa aceptable (área bajo la curva ROC mayor a 0,7).
Volviendo al modelo original, como se puede observar en la tabla 1, el EuroSCORE I calibró adecuadamente en varios años (2008, 2011, 2012, 2014, 2016, 2017, 2018 y 2019), por lo que para la comparación interna en esos años no hubiera sido necesario aplicar el modelo ajustado. De todas formas, se prefirió usar el mismo criterio hasta el 2020.
Otro aspecto interesante es el perfil de riesgo de la población uruguaya en el período evaluado (gráfico 1 para el modelo original y tabla 3 para el modelo ajustado). Teniendo en cuenta una mor talidad esperada del 4,8% para la población eu ropea original de 1999, en Uruguay la población fue siempre de un riesgo superior para todos los años considerados, pero con una tendencia leve hacia el aumento a lo largo de todo el período (por ejemplo, ME según modelo ajustado de 5,07% en 2007 y de 5,9% en el 2020, con un pico de 6,3% en 2017, tabla 3 ).
Pensamos que este trabajo tiene como fortale za presentar datos nacionales aplicando un mo delo de riesgo ampliamente utilizado en todo el mundo, lo que nos permite comparar con resulta dos a nivel internacional y, por otro lado, evaluar la performance comparativa interna a lo largo de un período de tiempo prolongado. Sin embargo, la mortalidad operatoria ajustada es uno más entre otros parámetros muy importantes que también son evaluados todos los años por el FNR y se en cuentran disponibles en la página web institucio nal.
El principal motivo por el cual se ha seguido aplicando el EuroSCORE I para evaluar resul tados es poder tener una perspectiva a lo largo del tiempo de la mortalidad con la misma herra mienta. Esto nos lleva inmediatamente, desde nuestro punto de vista, a la principal debilidad de este trabajo: aplicar un modelo de riesgo que tiene muchos años y que ha sido criticado en algunos aspectos, como la posibilidad de sobreestimar la mortalidad esperada fundamentalmente en pa cientes con una cirugía adicional o diferente a la cirugía coronaria15. Esto no parece suceder con nuestros resultados; sin embargo, la aplicación de modelos de riesgo más nuevos podría ayudarnos a esclarecer aún más el aspecto mencionado5.
Como desafío hacia el futuro, entonces, plan teamos poder aplicar otros modelos de riesgo usa dos en el plano internacional, más recientes, como es el EuroSCORE II, el STS o la elaboración de un modelo propio para la comparación interna que permitiría interpretar con otros criterios más ac tualizados la performance de los resultados de la cirugía cardíaca de adultos en el Uruguay.